本文主要是介绍【问题思考总结】二次型和二次曲面的关系【常数项的改变对曲面的影响】【图文】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题
今天做到一个题的时候发现,之前记的结论记错了,一个方程本来应该是双叶双曲面我记得,结果答案竟然是圆锥面,后来发现原因是常数项等于0或者不等于0的差别。因此,就这个问题我们来通过图文的方式探讨一下两种情况区别和联系,并且对所有情况做一个总结。
思考

可以看到,这里在后面标注了a>0,也是本题和上图情况区别的原因(题目为:yz+xz+xy=0)
因此,我们来看一下这几种情况分别是什么样的。
3正且相等
a>0
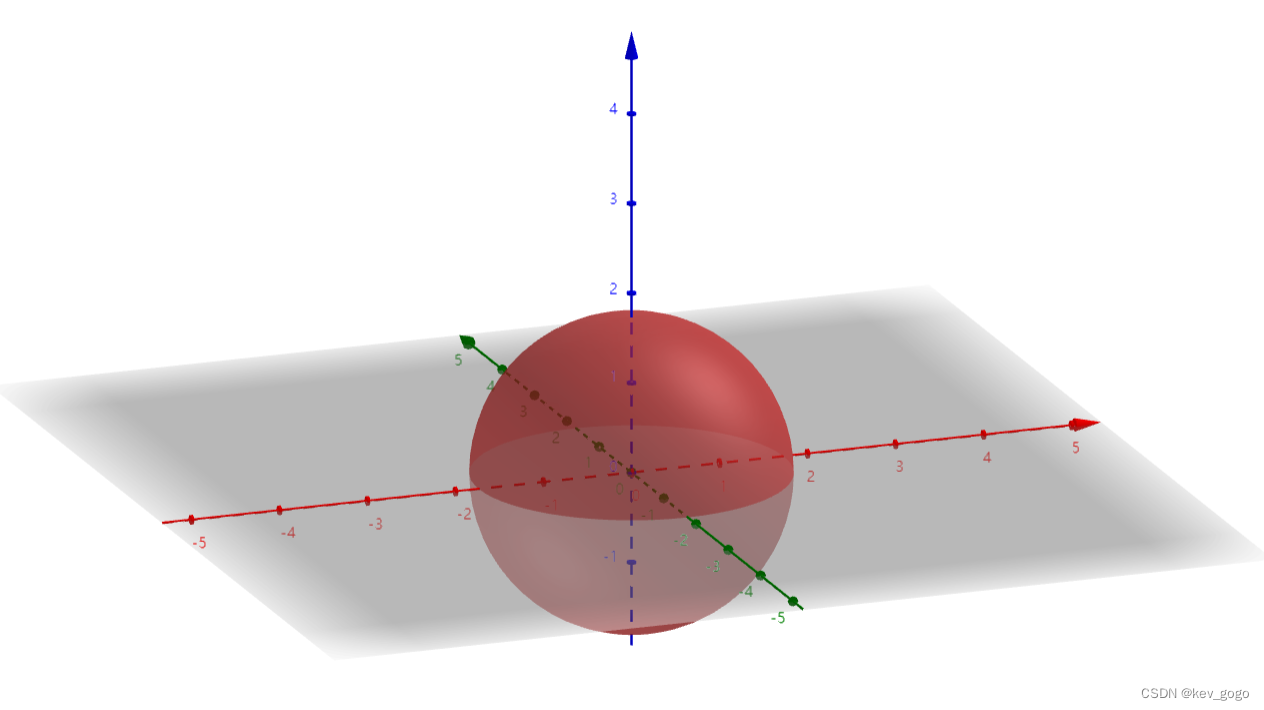
球面。
a=0
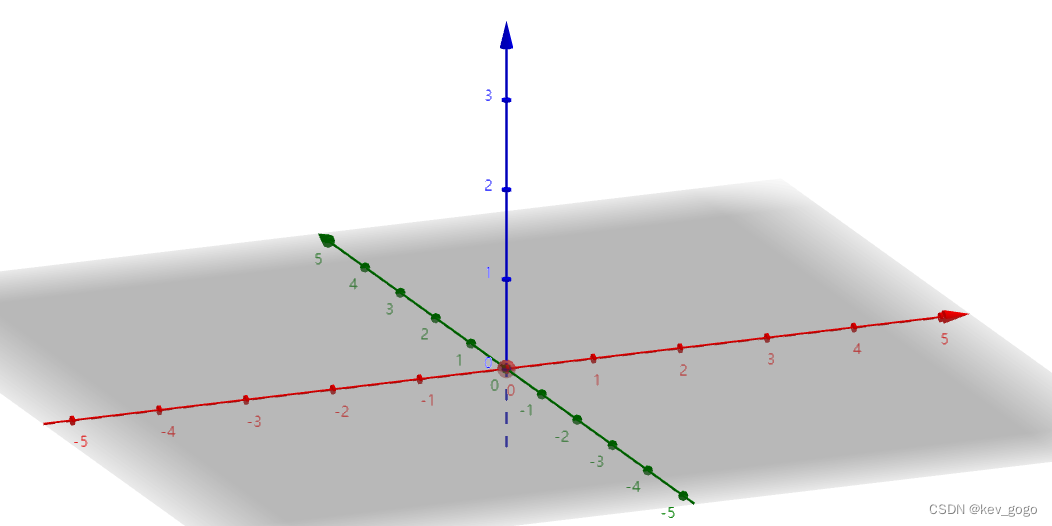
点。
a<0
不可能发生。
区别
可以看到a决定了球体的半径,当a=0的时候,原三维球面坍缩为一个点(原点)。
三正但不等

椭球面。
a=0
 。
。
点
a<0
不可能发生。
区别
可以看到a决定了椭球体的半径,当a=0的时候,原三维椭球面坍缩为一个点(原点)。
二正一负
a>0
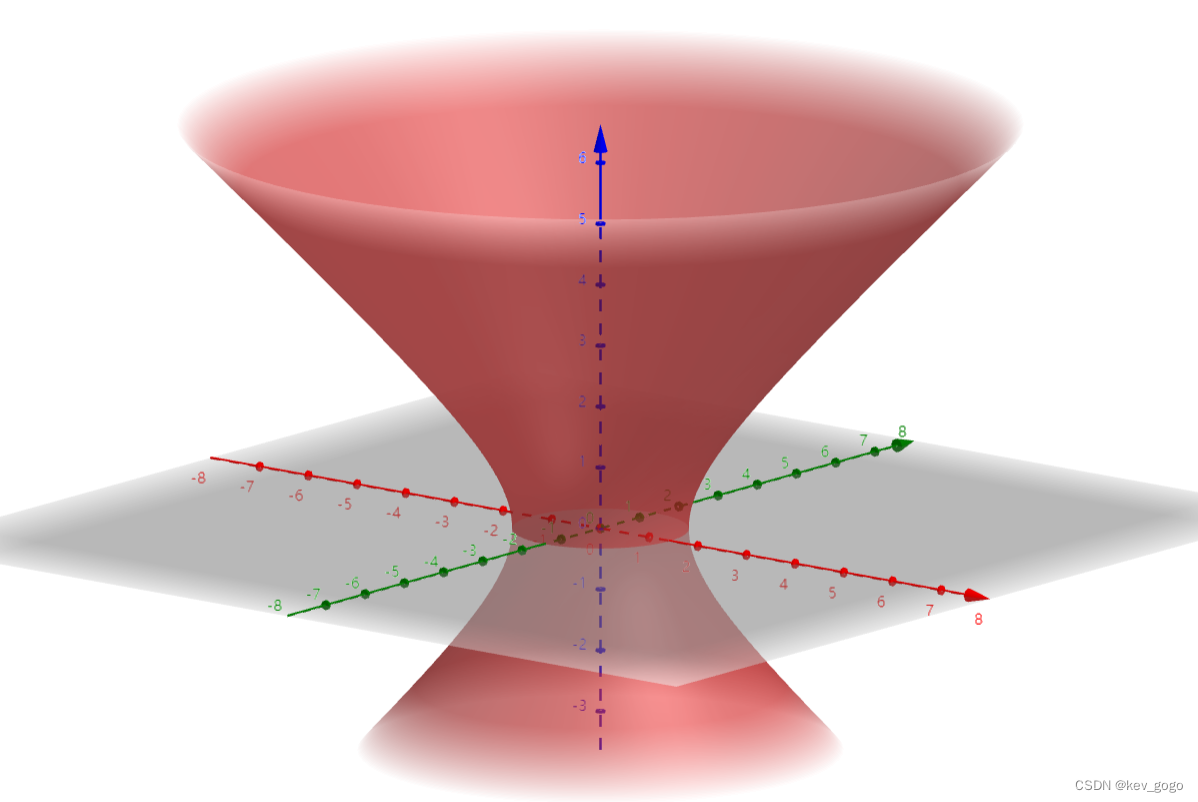
单页双曲面。
a=0

圆锥面。
a<0

双叶双曲面。
区别
可以看到,决定了和平面截得的面积大小,a=0时,面积为0,即为一个点,当a为负值时,单叶双曲面分离成为双叶双曲面,或者可以将等式两边乘一个负号,就变成了两负一正a>0的情况了。
二正一零正的相等
a>0
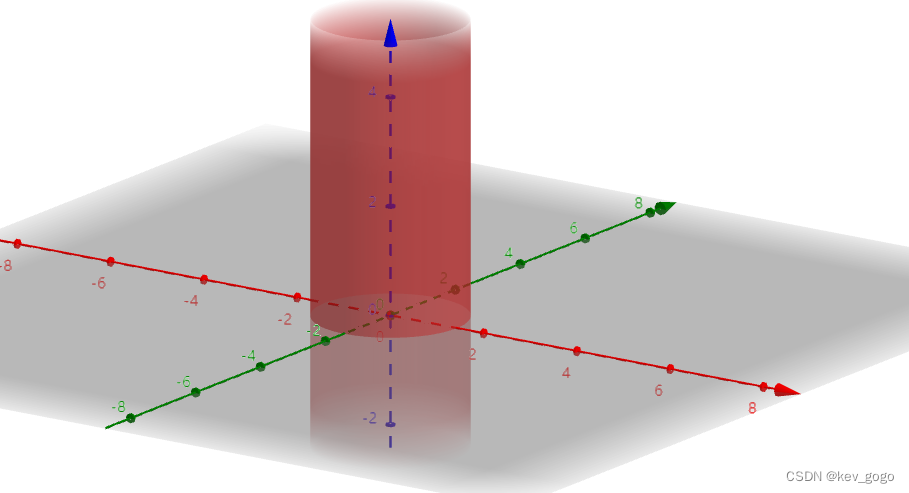
椭圆柱面。
a=0
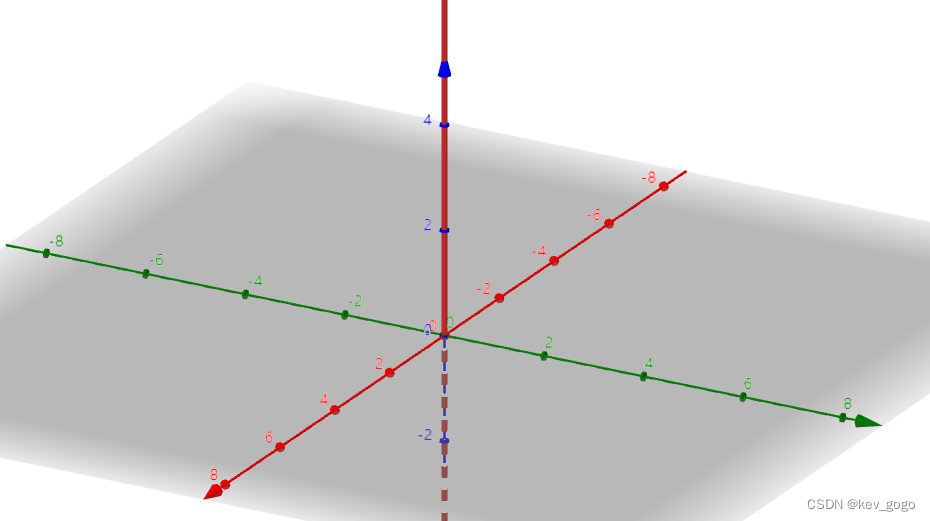
重合于z轴的直线。
a<0
不存在。
区别
和之前类似,a的取值决定了和平面截面面积的大小,当a=0时,截面面积为0,变为直线。
二正一零正的不等
a>0
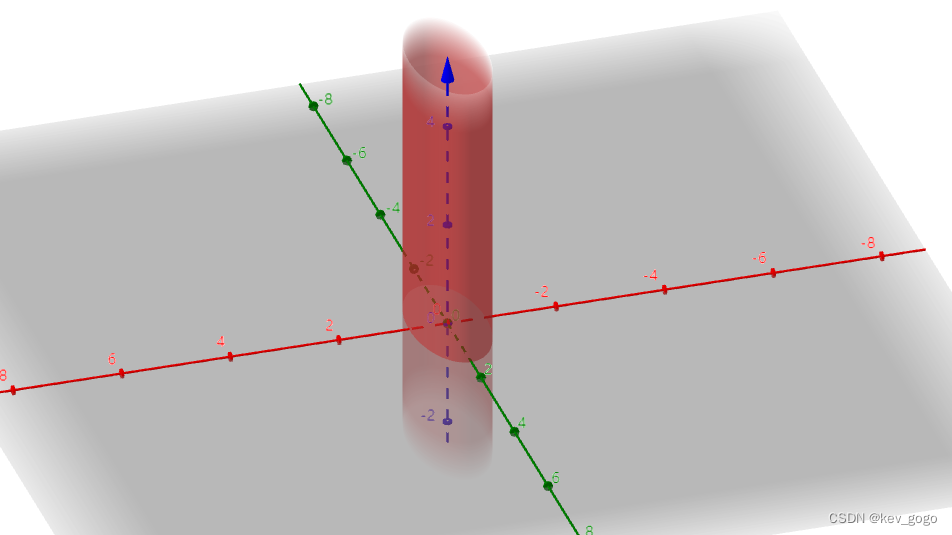
椭圆柱面。
a=0
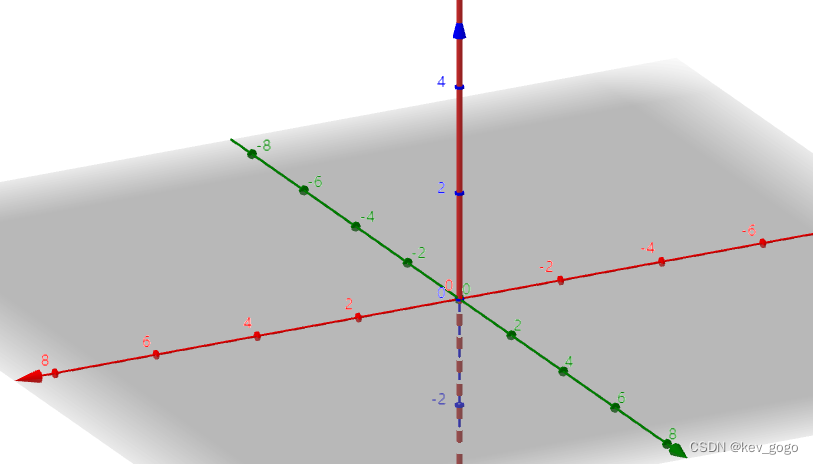
重合于z轴的直线。
a<0
不存在
区别
这里和上一种曲面的区别在于系数不同了,曲面发生了一定的伸缩变换。
一正二负
a>0

双叶双曲面。
a=0
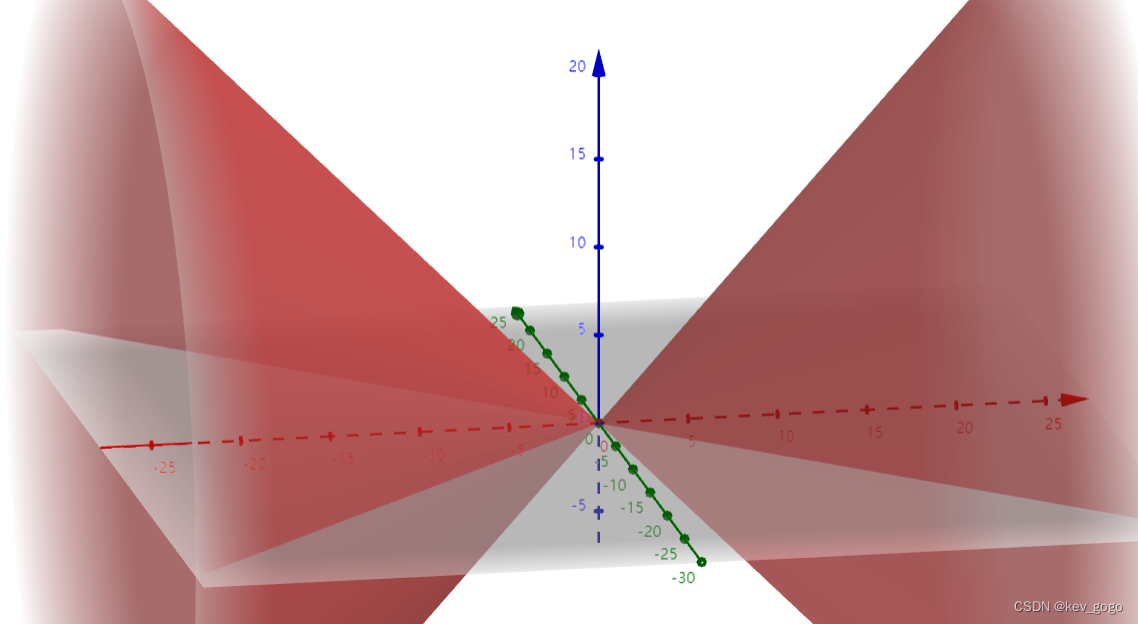
圆锥面。
a<0
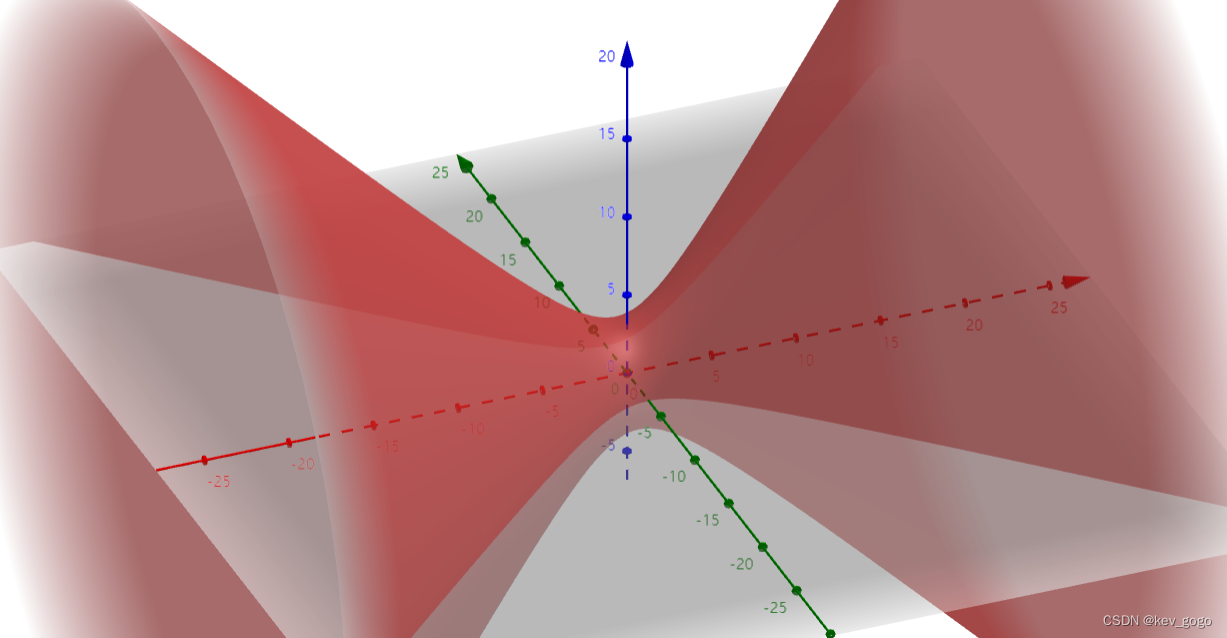
单叶双曲面。
区别
同之前一样,注意这里可以和两正一负的情况形成一个对应的关系。
一正一负一零
a>0
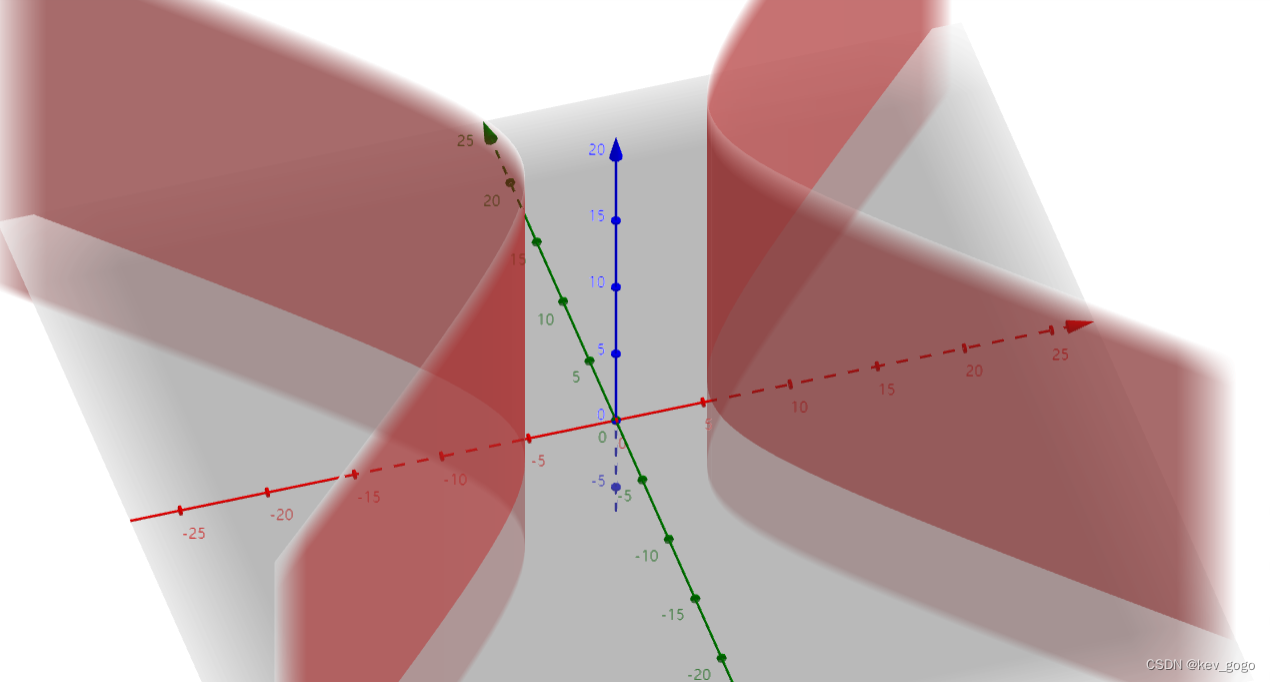
双曲柱面。
a=0
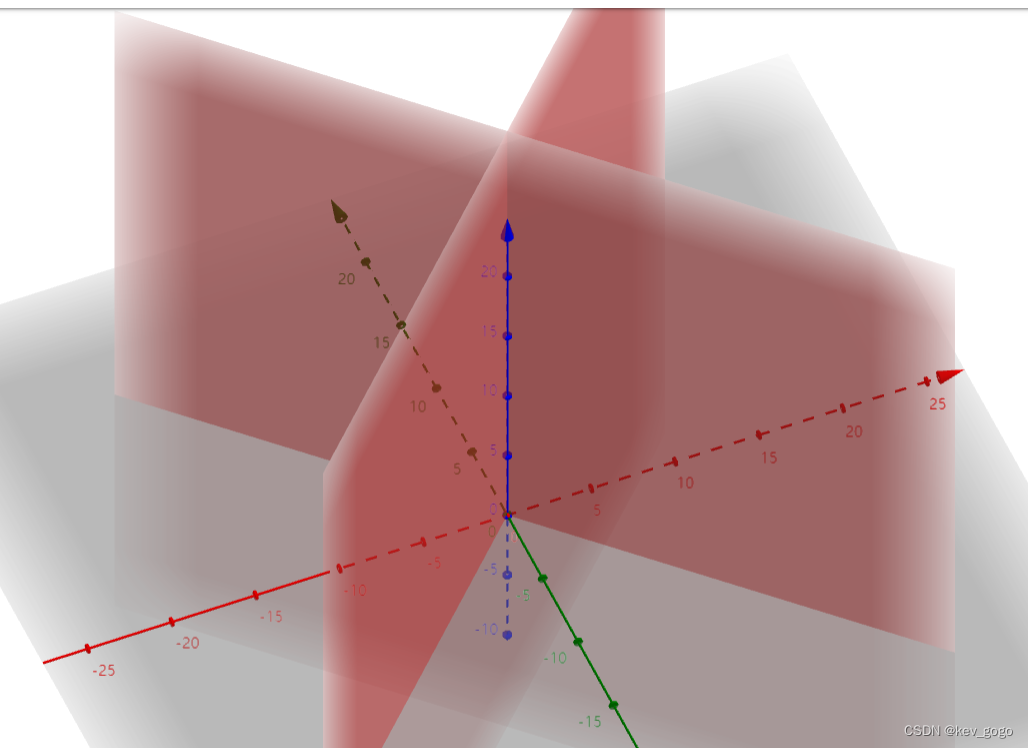
两个互相垂直的平面。
a<0
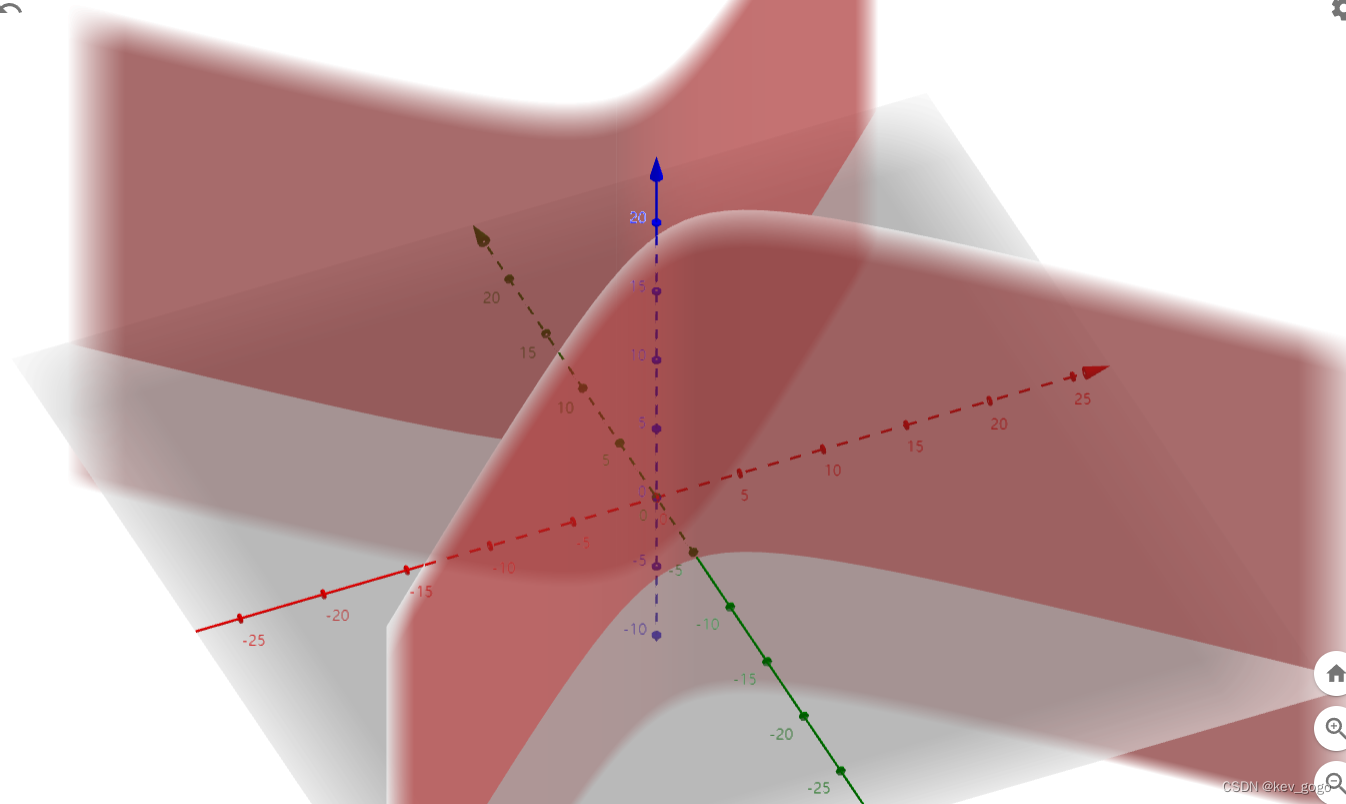
双曲柱面。
区别
a值得绝对值越大,弯曲程度越明显,当a值得绝对值等于0的时候,曲面不弯曲,变为平面。
tips
- 刚才柱面和抛物面混淆了。。。柱面的定义是直线沿着一条定曲线平行移动所形成的曲面,动直线称为柱面的直母线,定曲线称为柱面的准线。当准线是圆时所得柱面称为圆柱面。抛物面,是指抛物线旋转180°所得到的面。数学上的抛物线就是同一平面上到定点(焦点)的距离与到定直线(准线)的距离相等的点的集合 。抛物面是二次曲面的一种。抛物面有两种:椭圆抛物面和双曲抛物面。
总结
二次型可以通过正交变换变成标准型(将歪七扭八的图形一巴掌打正,并且可逆(正交)变换不改变二次型的正负惯性指数个数),然后即可用这些方法进行表示。
参考资料
[1]首图截自杨威线代课程
[2]绘图软件:https://www.geogebra.org/
[3]常见二次曲面:https://zhuanlan.zhihu.com/p/58917013
[4]百度百科(柱面,抛物面的定义)
这篇关于【问题思考总结】二次型和二次曲面的关系【常数项的改变对曲面的影响】【图文】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








