本文主要是介绍论文笔记--SimCSE: Simple Contrastive Learning of Sentence Embeddings,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文笔记--SimCSE: Simple Contrastive Learning of Sentence Embeddings
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 对比学习 Contrastive Learning
- 3.2 Unsupervised SimCSE
- 3.3 Supervised SimCSE
- 3.4 Anisotropy
- 3.5 Alignment and Uniformity
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:SimCSE: Simple Contrastive Learning of Sentence Embeddings
- 作者:Tianyu Gao, Xingcheng Yao, Danqi Chen.
- 日期:2021
- 期刊:arxiv preprint
2. 文章概括
文章给出了一种通过对比学习得到句子嵌入的方法:SimCSE。数值试验表明Unsupervised SimCSE在非监督STS任务上的表现超过SOTA,upervised SimCSE在监督STS任务上的表现超过SOTA。相比于SBERT[1],文章提出的SimCSE得到的句子嵌入具有更好的一致性和对齐性。
文章整体框架如下
S
3 文章重点技术
3.1 对比学习 Contrastive Learning
对比学习是一种学习句子嵌入的有效方法,旨在通过将语义相近的句子拉近,语义不同的句子推远。具体来说,假设我们有标注数据集 D = { ( x i , x i + ) } i = 1 m \mathcal{D} = \{(x_i, x_i^+)\}_{i=1}^m D={(xi,xi+)}i=1m,其中每一对样本 ( x i , x i + ) (x_i, x_i^+) (xi,xi+)表示语义相关的正样本,令 h i \boldsymbol{h_i} hi和 h i + \boldsymbol{h_i}^+ hi+分别表示 x i x_i xi和 x i + x_i^+ xi+对应的向量表示,则针对每个大小为 N N N的mini-batch(即 N N N个样本对),对比学习的目标为 l i = − log e s i m ( h i , h i + ) / τ ∑ j = 1 N e s i m ( h i , h j + ) / τ l_i = -\log \frac{e^{sim(\boldsymbol{h_i}, \boldsymbol{h_i}^+)/\tau}}{\sum_{j=1}^N e^{sim(\boldsymbol{h_i}, \boldsymbol{h_j}^+)/\tau}} li=−log∑j=1Nesim(hi,hj+)/τesim(hi,hi+)/τ,其中 τ \tau τ为温度参数,当 τ \tau τ比较小的时候,可以令正负样本的差异增大; s i m ( h i , h j + ) sim(\boldsymbol{h_i}, \boldsymbol{h_j}^+) sim(hi,hj+)表示 h i , h i + \boldsymbol{h_i}, \boldsymbol{h_i}^+ hi,hi+之间的cosine相似度, h i , h i + \boldsymbol{h_i}, \boldsymbol{h_i}^+ hi,hi+为 x i , x i + x_i, x_i^+ xi,xi+输入BERT[2]/RoBERTa[3]得到的嵌入,然后我们根据上述训练目标将BERT/RoBERTa的参数进行微调。
3.2 Unsupervised SimCSE
SimCSE的思想非常简单,即我们将相同的句子做不同的随机掩码,作为对比学习模型中的正样本输入。比如我们有句子集合 { x i } \{x_i\} {xi},则我们令 x i + = x i x_i^+=x_i xi+=xi,但分别将 x i , x i + x_i, x_i^+ xi,xi+作为独立的输入进行不同的dropout masks输入到Transformer模型。具体来讲,我们对 x i , x i + x_i, x_i^+ xi,xi+分别生成随机mask z i , z i + z_i, z_i^+ zi,zi+用于dropout token,然后我们得到它们各自的向量嵌入 h i z i , h i z i + \boldsymbol{h}_i^{z_i}, \boldsymbol{h}_i^{z_i^+} hizi,hizi+,从而我们的损失函数变为 l i = − log e s i m ( h i z i , h i z i + ) / τ ∑ j = 1 N e s i m ( h i z i , h i z j + ) / τ l_i = -\log \frac{e^{sim(\boldsymbol{h}_i^{z_i}, \boldsymbol{h}_i^{z_i^+})/\tau}}{\sum_{j=1}^N e^{sim(\boldsymbol{h}_i^{z_i}, \boldsymbol{h}_i^{z_j^+})/\tau}} li=−log∑j=1Nesim(hizi,hizj+)/τesim(hizi,hizi+)/τ.
我们可以将dropout mask视为一种最小化的数据增强方法。为了验证该方法的性能,我们将其与裁剪、单词删除、删除一个单词、同义词替换和MLM这些数据增强方法进行对比,发现我们的dropout方法表现最好。

3.3 Supervised SimCSE
SimCSE可以利用标注数据进一步提升模型性能。文章考虑NLI任务数据。NLI任务中,给定一对句子,它们的关系为entaiment(蕴含), neutral(中立)或contradiction(对立)。训练时,我们可以只考虑entailment的样本作为正样本对,此时可直接使用上述对比损失函数。
或者我们可以将对立的标注也引入模型,此时我们将样本对拓展为 ( x i , x i + , x i − ) (x_i, x_i^+, x_i^-) (xi,xi+,xi−),训练目标定义为 l i = − log e s i m ( h i , h i + ) / τ ∑ j = 1 N e s i m ( h i , h j + ) / τ + e s i m ( h i , h j − ) / τ l_i = -\log \frac{e^{sim(\boldsymbol{h_i}, \boldsymbol{h_i}^+)/\tau}}{\sum_{j=1}^N e^{sim(\boldsymbol{h_i}, \boldsymbol{h_j}^+)/\tau} + e^{sim(\boldsymbol{h_i}, \boldsymbol{h_j}^-)/\tau}} li=−log∑j=1Nesim(hi,hj+)/τ+esim(hi,hj−)/τesim(hi,hi+)/τ.
实验证明,负样本(hard negative)的引入可有效的增强模型表现:

3.4 Anisotropy
最近的一些论文表明BERT产生的语言表示会存在各向异性问题,即生成的向量在高维空间中类似一个锥体,这可能会严重限制词向量的表达能力。
解决上述问题的一种简单方法为后处理,我们可以减轻一些主要成分从而不让一些特征对整体的影响过大,或者我们可以将嵌入映射到一个各项同性的空间。另一种方法为在训练过程增加正则项。
在本文中,我们可以证明我们提出的dropout方法可以有效地缓解各向异性问题。事实上,上述增加了hard negative的对比损失函数可写成 − 1 τ E ( x , x + ) ∈ P p o s [ f ( x ) T f ( x + ) ] + E x ∈ P d a t a [ log E x − ∈ P d a t a [ e f ( x ) T f ( x + ) / τ ] ] -\frac 1\tau \mathbb{E}_{(x, x^+)\in \mathcal{P}_{pos}} \left[f(x)^Tf(x^+)\right] + \mathbb{E}_{x \in \mathcal{P}_{data}} \left[\log \mathbb{E}_{x^- \in \mathcal{P}_{data}} \left[e^{f(x)^Tf(x^+)/\tau}\right]\right] −τ1E(x,x+)∈Ppos[f(x)Tf(x+)]+Ex∈Pdata[logEx−∈Pdata[ef(x)Tf(x+)/τ]],其中第一项是为了让正样本尽可能相似,第二项是为了让负样本尽可能拉远。当 P d a t a \mathcal{P}_{data} Pdata是在 { x i } i = 1 m \{x_i\}_{i=1}^m {xi}i=1m中均匀采样有限次时,上式第二项可写作 E x ∈ P d a t a [ log E x − ∈ P d a t a [ e f ( x ) T f ( x + ) / τ ] ] = 1 m ∑ i = 1 m log ( 1 m ∑ j = 1 m e h i T h j / τ ) \mathbb{E}_{x \in \mathcal{P}_{data}} \left[\log \mathbb{E}_{x^- \in \mathcal{P}_{data}} \left[e^{f(x)^Tf(x^+)/\tau}\right]\right] \\ = \frac 1m \sum_{i=1}^m \log \left(\frac 1m \sum_{j=1}^m e^{\boldsymbol{h_i}^T \boldsymbol{h_j}/\tau}\right) Ex∈Pdata[logEx−∈Pdata[ef(x)Tf(x+)/τ]]=m1i=1∑mlog(m1j=1∑mehiThj/τ)。再由Jensen不等式[5]和 log \log log为凹函数,我们有 log ( 1 m ∑ j = 1 m e h i T h j / τ ) ≥ ∑ j = 1 m 1 m log ( e h i T h j / τ ) = 1 m τ h i T h j \log \left(\frac 1m \sum_{j=1}^m e^{\boldsymbol{h_i}^T \boldsymbol{h_j}/\tau}\right) \ge \sum_{j=1}^m \frac 1m \log (e^{\boldsymbol{h_i}^T \boldsymbol{h_j}/\tau}) = \frac 1{m\tau} \boldsymbol{h_i}^T \boldsymbol{h_j} log(m1j=1∑mehiThj/τ)≥j=1∑mm1log(ehiThj/τ)=mτ1hiThj,从而损失函数的第二项满足 E x ∈ P d a t a [ log E x − ∈ P d a t a [ e f ( x ) T f ( x + ) / τ ] ] ≥ 1 m 2 τ ∑ i , j h i T h j \mathbb{E}_{x \in \mathcal{P}_{data}} \left[\log \mathbb{E}_{x^- \in \mathcal{P}_{data}} \left[e^{f(x)^Tf(x^+)/\tau}\right]\right]\ge \frac 1{m^2\tau} \sum_{i,j}\boldsymbol{h_i}^T \boldsymbol{h_j} Ex∈Pdata[logEx−∈Pdata[ef(x)Tf(x+)/τ]]≥m2τ1i,j∑hiThj.记 W = ( h 1 T , … , h m T ) T W = (\boldsymbol{h_1}^T,\dots, \boldsymbol{h_m}^T)^T W=(h1T,…,hmT)T,考虑到 h i \boldsymbol{h_i} hi式正则化之后的向量,我们有 W W T WW^T WWT的对角线上都是1。事实上,考虑实对称矩阵 W W W的特征分解 W = Q Λ Q − 1 W=Q\Lambda Q^{-1} W=QΛQ−1,其中 Q Q Q为正交矩阵,则 t r ( W W T ) = t r ( Q Λ Q − 1 ( Q Λ Q − 1 ) T ) = t r ( Q Λ Q − 1 Q − 1 T Λ T Q T ) = t r ( Q Λ Λ T Q T ) = ∑ j λ j tr(WW^T) = tr(Q\Lambda Q^{-1}(Q\Lambda Q^{-1})^T) = tr(Q\Lambda Q^{-1}{Q^{-1}}^T \Lambda^TQ^T ) \\= tr(Q\Lambda \Lambda^T Q^T)=\sum_j \lambda_j tr(WWT)=tr(QΛQ−1(QΛQ−1)T)=tr(QΛQ−1Q−1TΛTQT)=tr(QΛΛTQT)=j∑λj,另一方面我们有 t r ( W W T ) = n tr(WW^T)=n tr(WWT)=n,从而 ∑ j λ j = n \sum_j \lambda_j=n ∑jλj=n。又由Merikoski定力,可得到 S u m ( W W T ) Sum(WW^T) Sum(WWT)是其最大特征值的一个上界,从而当我们最小化损失函数的时候,损失函数的第二项自然会变小,故有 1 m 2 τ ∑ i , j h i T h j = 1 m 2 τ S u m ( W W T ) ≥ λ l a r g e s t \frac 1{m^2\tau} \sum_{i,j} \boldsymbol{h_i}^T \boldsymbol{h_j}=\frac 1{m^2\tau}Sum(WW^T)\ge \lambda_{largest} m2τ1∑i,jhiThj=m2τ1Sum(WWT)≥λlargest会变小。总结下来,我们通过沿着损失函数减小的方向学习,可以使得 W W T WW^T WWT的最大特征值被削弱,而由于所有特征值之和是定值,故其它特征值会增加,从而有效提高句嵌入的uniformity
3.5 Alignment and Uniformity
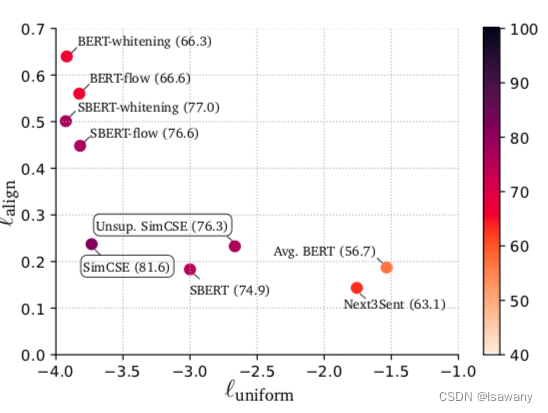
对比学习有两个关键的度量指标:Alignment和Uniformity。Alignment表示正样本之间的距离,其值越小越好。Uniformity表示随机采样的样本是否均匀分布,其值越小越好。具体定义如下 l a l i g n : = E ( x , x + ) ∈ P p o s ∥ f ( x ) − f ( x + ) ∥ 2 l u n i f o r m : = log E ( x , y ) ∼ i . i . d . P d a t a e − 2 ∥ f ( x ) − f ( x + ) ∥ 2 l_{align} := \mathbb{E}_{(x, x^+)\in \mathcal{P}_{pos}} \Vert f(x) - f(x^+)\Vert^2 \\l_{uniform} := \log \mathbb{E}_{(x, y)\overset{i.i.d.}{\sim} \mathcal{P}_{data}} e^{-2\Vert f(x) - f(x^+)\Vert^2} lalign:=E(x,x+)∈Ppos∥f(x)−f(x+)∥2luniform:=logE(x,y)∼i.i.d.Pdatae−2∥f(x)−f(x+)∥2。
上述我们已经证明dropout可以缓解各向异性,自然地,uniformity也会随之提升。数值实验也表明,SimCSE可有效增强学习到的句子嵌入的Alignment和Uniformity:
4. 文章亮点
文章提出了SimCSE,一种基于dropout的数据增强方法。通过该方法训练的BERT系列模型在STS任务上取得了新的SOTA。且文章提出了非监督和监督SimCSE方法,以供不同场景的下游任务学习。SimCSE得到的句子嵌入给出了更好的Alignment和Uniformity,且有效缓解了BERT模型产生的各向异性,从而高效地给出句子表达。
5. 原文传送门
SimCSE: Simple Contrastive Learning of Sentence Embeddings
6. References
[1] 论文笔记–Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks
[2] 论文笔记–BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
[3] 论文笔记–RoBERTa: A Robustly Optimized BERT Pretraining Approach
[4] 各向异性
[5] Jensen 不等式
这篇关于论文笔记--SimCSE: Simple Contrastive Learning of Sentence Embeddings的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








