[MATLAB]符号对象建立运算以及符号矩阵(syms,factor,assume,collect)

本实验源于中南大学《科学计算与MATLAB语言》，包括三个内容，内容如下：

• 符号对象的建立
• 符号对象的运算
• 符号矩阵

符号对象的建立

• sym函数
  sym函数用于建立单个符号对象，其常用调用格式为：

符号对象名=sym(A)

将由A来建立符号对象，其中，A可以是一个数值常量、数值矩阵或数值表达式(不加单引号),此时符号对象为一个符号常量；A也可以是一个变量名(加单引号),这时符号对象为一个符号变量.
下面给出两个例子
1、将符号常量2赋给t，参与四则运算
2、 将常量pi/3转化为符号对象求正弦值
3、将pi/3做数值计算，得到真实的sin正弦值
代码如下：

>> t=sym(2);
>> t+1/2ans =5/2>> sin(sym(pi/3))ans =1/2*3^(1/2)>> sin(pi/3)ans =0.8660>> 

总结：第一个求的是数值，第二个计算符号常量是一个表达时，第三个计算常量是一个数值
下面来两个符号变量的例子

>> a=5;
>> b=-8;
>> x=sym('a');
>> y=sym('b');
>> w=(a+b)*(a-b)w =-39>> s=(x+y)*(x-y)s =(a+b)*(a-b)>> 

大家有没有体会到，反正博主已经体会到了，这个变量能计算，符号常量貌似只能出个表达式，也就是符号计算的结果是一个精确的数学表达式，数值计算只能是数值。

>> eval(s)ans =-39>> 

没有我matlab函数干不了的，再来一个eval函数！

• syms命令
  syms命令可以一次定义多个符号变量，其一般调用格式如下：

syms 符号变量1 符号变量2 ... 符号变量名n

其中，变量名不能加单引号，相互之间用空格隔开。

符号对象的运算

四则运算

符号表达式的四则运算与数值运算一样，用+、-、*、/、^运算符实现，其运算结果依然是一个符号表达式.

>> syms x;
>> f=2*x^2+3*x-5;
>> g=x^2-x+7;
>> f+gans =3*x^2+2*x+2>> 

这段代码就是利用符号对象创建表达式然后进行两个多项的加法，是不是非常神奇？

关系运算

• 6种关系运算符：<、<=、>、>=、==、~=
• 对应的6个函数：lt()、le()、gt()、ge()、eq()、ne()
  若参与运算的是符号表达式，其结果是一个符号表达式：若参与运算的是符号矩阵，其结果是由符号关系表达式组成的矩阵.
  在进行符号对象的运算前，可用assume函数符号对象设置值域，函数调用格式为：

assume(condition)
assume(expr,set)

第一种格式指定变量满足条件condition,第二种格式指定表达式expr属于集合set。

syms x;
assume(x<0);
abs(x)==xassume(x,'positive');
abs(x)==x

逻辑运算

• 3种逻辑运算符:)(与)、|（或）和~（非）。
• 4个逻辑运算函数：and()、or()、not()、xor().

syms x
and(x<0,x>10);

因式分解与展开运算

MATLAB提供了符号表达式进行因式分解、展开、合并的函数，函数的调用格式为：

factor(s):对符号表达式s分解因式
expand(s):对符号表达式s进行展开
collect(s):对符号表达式s合并同类项
collect(s,v):对符号表达式s按变量v合并同类项

>> syms a b;
>> s=a^3-b^3;
>> factor(s)ans =-(b-a)*(b^2+b*a+a^2)>> 

>> factor(12)ans =2     2     3>> 

我用c实现的，结果matlab都已经实现好了，太强了！

梅森素数的验证问题

数学的理论领域里要研究大素数，而大素数都是梅森素数，梅森素数的寻找也就变得为大素数提供了方向！

>> syms p;
>> m=2^p-1;
>> p=19;
>> m19=eval(m)m19 =524287>> factor(m19)ans =524287>> 
>> p=23;
>> m23=eval(m)m23 =8388607>> factor(m23)ans =47      178481>> p=29;
>> m29=eval(m)m29 =536870911>> factor(m29)ans =233        1103        2089>> p=31;
>> m31=eval(m)m31 =2.1475e+009>> factor(m31)ans =2.1475e+009>> 

总结：M19/M31不能被分解，所以是素数
M23/M29能被分解，所以不是素数

其他运算

提取有理分式的分子分母:[n,d]=nuden(s)
提取符号表达式的系数:c=coeffs(s,x)
符号表达式化简:simplify(s)
符号多项式与多项式系数向量之间的转换：
符号多项式转换为多项式系数向量:p=sym2poly(s)
多项式系数向量转换为符号多项式:s=poly2sym(p)

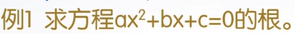
步骤：

1. 建立方程
2. 取出系数
3. 反转系数
4. 求根roots，打完收工！

>> syms a b c x;
>> f=a*x^2+b*x+c>> g=coeffs(f,x)>> g=g(end:-1:1)>> roots(g)

符号运算种变量的确定

1. 如果没有明确指定自变量，MATLAB将按以下原则确定主变量并对其相应运算：
   ①寻找除i,j之外，在字母顺序上最接近x的小写字母
   ②若表达式中有两个符号变量与x的距离相等，则ASCII码大者优先。

2. symvar()函数可以用于查找一个符号表达式中符号变量，函数的调用格式为：

symvart(s,n)

函数返回符号表达式s中n个符号变量。因此，可以用symvar(s1j)查找表达式s的主变量

符号矩阵

符号矩阵也是一种符号表达式，所以符号表达式运算都可以在矩阵意义下进行。
注意：这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。

>> syms a b x y alp;
>> m=[a^3-b^3,sin(alp)^2+cos(alp)^2;(15*x*y-3*x^2)/(x-5*y),78]m =[                a^3-b^3,  sin(alp)^2+cos(alp)^2]
[ (15*x*y-3*x^2)/(x-5*y),                     78]>> simplify(m)ans =[ a^3-b^3,       1]
[    -3*x,      78]>> 

对于齐次线性方程组Ax=0，当rank(A)<n或|A|=0时，齐次线性方程组有非零解。

>> syms lamda;
>> A=[1-lamda,-2,4;2,3-lamda,1;1,1,1-lamda];
>> D=det(A);
>> factor(D)ans =-lamda*(lamda-2)*(-3+lamda)>> 

根据线性代数的知识，可以看出，当其为0，2，3即有非零解。