double operator[](int i)_Stata: 双栏模型简介 (Double-hurdle model)

本文主要是介绍double operator[](int i)_Stata: 双栏模型简介 (Double-hurdle model)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

编译：李琼琼 (山东大学)
Stata 连享会：知乎 | 简书 | 码云 | CSDN

连享会-知乎推文列表

Note: 助教招聘信息请进入「课程主页」查看。

因果推断-内生性专题 ⌚ 2020.11.12-15
主讲：王存同 (中央财经大学)；司继春(上海对外经贸大学) 课程主页： https://gitee.com/arlionn/YG | 微信版

空间计量专题 ⌚ 2020.12.10-13
主讲：杨海生 (中山大学)；范巧 (兰州大学) 课程主页： https://gitee.com/arlionn/SP | 微信版

连享会 最新专题 直播

背景介绍
1. 双栏模型 (Double-hurdle model) 介绍
- 1.1 Tobit 模型
- 1.2 Double - hurdle 模型
- 1.3 用图形解释 double hurdle 模型
- 1.4 Double - hurdle 模型的特殊形式
2. 模型的 Stata 实现
- 2.1 dhreg 命令介绍
- 2.2 基于模拟分析的范例
- 2.3 模型估计
3. 面板双栏模型 (Panel-hurdle model)
- 3.1 面板双栏模型基本原理
- 3.2 面板双栏模型的 Stata 实现
- 3.3 基于模拟分析的范例
参考文献
关于我们

本文主要翻译自如下论文，并进行了适当的补充和调整. Source： Engel C, Moffatt P G. Dhreg, xtdhreg, and bootdhreg: Commands to implement double-hurdle regression[J]. Stata Journal, 2014, 14(4):778-797. [PDF]

背景介绍

双栏模型 (Double-hurdle model) 是由 Cragg (1971) 提出的：对于一个活动的参与，个体决策是由两部分组成的。第一个门槛 (hurdle), 决定个体是否是零类型；第二个门槛 (hurdle) 是在第一个阶段是非零的条件下，决定个体对活动的参与程度。这个模型的关键特征是这里有两种类型的零观测值，一种是无周围的环境如何变化他的选择都是零，另一种是他可以有非零选择但是目前的环境导致他选择零，后者也被称为归并零 (Tobin,1958) 。因此，双栏模型除了包括自然的零类型外，还允许零的概率由观测值的个体决定的。本质上，Double-hurdle 模型是 Tobit 模型的延续。本文主要分三部分内容进行介绍：

1 双栏模型介绍
2 模型的实现
3 面板双栏模型

1. 双栏模型 (Double-hurdle model) 介绍

介绍双栏模型最自然的开始是先介绍 Tobit 模型，再来引入双栏模型。

1.1 Tobit 模型

Tobit 模型又被称为归并回归模型 (censored regression model)，根据 limit 的设置分为左归并 (lower censoring) 和右归并 (upper censoring)，左归并指事先设置一个最小值 A，当被解释变量低于这个值时则自动等于 A。如果最低的 limit 为 0 时，被称为零归并 (zero censoring)。

上面的公式中潜变量

(最终无法直接被看到）代表个体

希望做出的贡献 (latent contribution)，这个潜在贡献可以为负值，但是试验规则认为只要为负值最终的贡献都归为 0 (规则如下）：

这里以零归并举例，采用对数似然函数，估计模型如下：

其中

为示性函数，当下标所表示的条件正确时取值为 1，否则为 0。通过使

最大化来求出

和

。

1.2 Double - hurdle 模型

Double - hurdle 模型有两个阶段，这两个阶段分别采用 probit 估计和 tobit 估计：

在第一个阶段 (hurdle)，被解释变量 (

) 是二元变量,由潜变量

决定。

在第二个阶段 (hurdle), 被解释变量

是零或者正数，非常像

Tobit 模型 (Ⅰ)。

双栏模型对数似然函数为：

上式中，双栏模型的第二个阶段给

设置了最小值 0 ，当然也可以将最小值设置为其他数

, 都被称为

lower hurdle。若最小值为

，对数似然函数的变为：

若双栏模型是 upper hurdle 型，即第二个阶段设置一个最大值

，所有超过

的值都等于

，小于

的值则不改变，那么此时模型变为：

1.3 用图形解释 double hurdle 模型

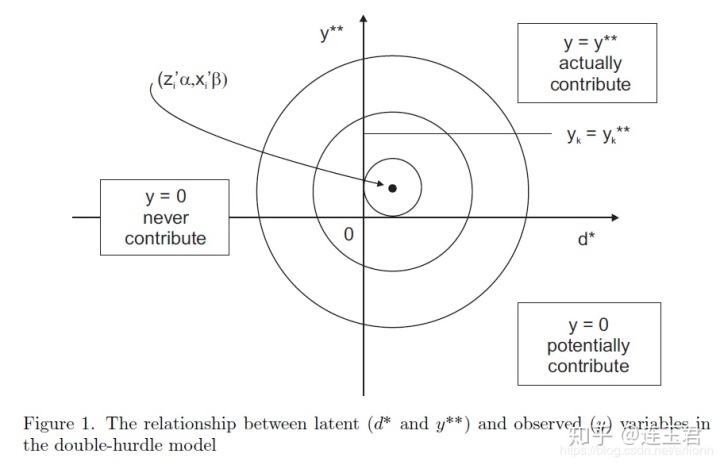
上图中的的同心圆是

和

的联合分布，这个同心圆是以

为中心并根据解释变量的变动进行移动。在第二、三象限，由于

小于 0，

一直为 0，表现为个体永远不会 contribute；在第四象限，

大于 0, 但是

小于 0，所以

暂时为 0，会随着

变量的变动的而可能大于 0；在第一象限，

为正数，个体实际做了 contribution。

1.4 Double - hurdle 模型的特殊形式

如果模型第一阶段，只有截距而没有解释变量，

, 则对数似然函数变为：

将

,此时模型就变成了

p-tobit 模型，即认为有一定比例

的样本可能会 contribute，而永远不会 contribute 的样本占

的比例。

p-tobit 模型最先由 (Deaton and Irish, 1984) 提出。

连享会 最新专题 直播

2. 模型的 Stata 实现

2.1 dhreg 命令介绍

我们可以使用 dhreg 命令来实现双栏模型的估计。在 Stata 命令窗口中输入 help dhreg 命令即可查看其完整帮助文件。dhreg 命令的基本语法为：

dhreg depvar indepvars [if] [in] [, up ptobit hd(varlist) millr]

各项的含义如下：

depvar: 表示被解释变量，即最终的可观测的
indepvars：表示关键的解释变量，即决定
(潜变量) 的解释变量
up：将模型设置为右归并，并且设置
最大值（默认为左归并）
ptobit：将双栏模型设置为 p-tobit 模型
hd(varlist): 表示第一栏中决定
的解释变量
millr：用逆米尔斯比率来控制扰动项的相关性

2.2 基于模拟分析的范例

我们通过模拟生成的数据来对 dhreg 命令的使用进行介绍，下面是数据生成的过程 (DGP)：

上面第一个公式生成的潜变量

即为第一个栏 (hurdle)，是由服从均匀分布的外生变量

和扰动项

决定的。第二个公式生成潜变量

是第二个栏 (hurdle)，是由外生变量

和扰动项

决定的。当前面两个栏都被跨过时，就可以观察到变量

(可观测变量）的取值 (非 0)，否则

为 0。

clear all
set obs 1000
set seed 123   // 设置种子，为了使每次重复模拟过程的结果相同
gen z_i = uniform()   //  z_i 服从（0,1)均匀分布
set seed 1234
gen x_i = uniform()
set obs 1000
set seed 12345  
gen e_i2 = invnormal(uniform())  // e_i2 服从标准正态分布
set seed 12435
gen n_i = invnormal(uniform())
gen e_i1 = 0.5*e_i2 + sqrt(1-0.5*0.5)*n_i
gen d_i = 0
replace d_i = 1 if -2 + 4*z_i + e_i1 > 0
gen y_i2 = 0.5 + 0.3*x_i + e_i2
gen y_i1 = 0
replace y_i1 = y_i2 if y_i2 > 0
gen y_i = d_i*y_i1
save data_process1.dta, replace  // 保存一份模拟数据

数据效果如下：

use "data_process1.dta", clear
hist y_i if d_i == 1,title(Conditional on passing first hurdle) scheme(sj)
graph save y_i_1.gph, replace
hist y_i ,title(All Data) scheme(sj)
graph save y_i_2.gph, replace
gr combine  y_i_1.gph  y_i_2.gph
graph save y_i.png, replace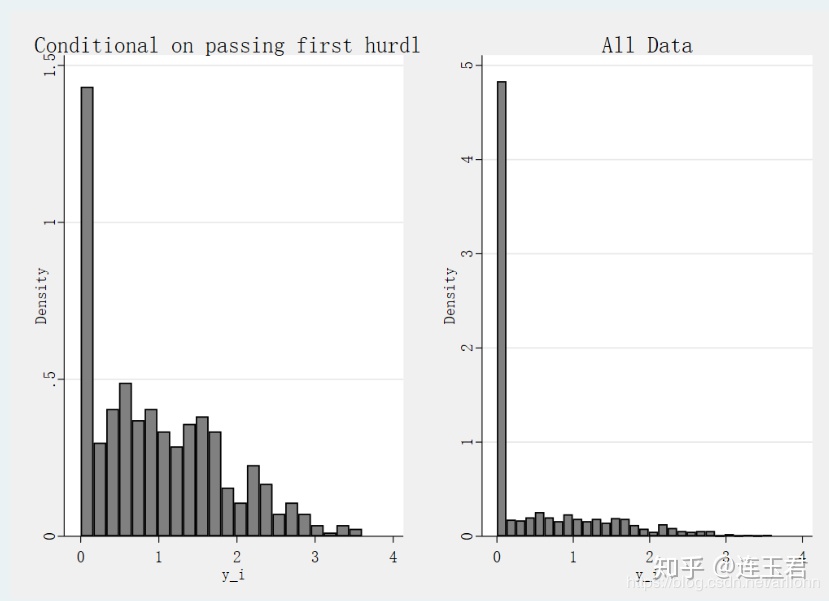

从左图可以看出有很多观测值通过了第一栏(即

), 但是由于潜变量

为 0，导致了最终观测值为 0。而更多的

为 0 的观测值是因为没有通过第一栏 (即

)。

2.3 模型估计

我们先进行传统的 tobit 估计, 再使用 dhreg 进行估计，然后对这两种估计结果进行比较。

. use "data_process1.dta", clear
. tobit y_i x_i, ll(0)
Tobit regression                                Number of obs     =      1,000Uncensored     =        413
Limits: lower = 0                                  Left-censored  =        587upper = +inf                               Right-censored =          0LR chi2(1)        =       3.49Prob > chi2       =     0.0619
Log likelihood = -1129.3849                     Pseudo R2         =     0.0015------------------------------------------------------------------------------y_i |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------x_i |   .3617779   .1939403     1.87   0.062    -.0187992    .7423551_cons |  -.4709888   .1194536    -3.94   0.000    -.7053975   -.2365801
-------------+----------------------------------------------------------------var(e.y_i)|    2.40666    .191884                      2.058097    2.814257
------------------------------------------------------------------------------

接着是进行 dhreg 估计：

dhreg y_i x_i, hd(z_i)(output omitted)maximum likelihood estimates of double hurdle modelN = 1000
log likelihood = -984.07209
chi square hurdle equation = 67.264411
p hurdle equation = 2.374e-16
chi square above equation = 4.8518223
p above equation = .02761694
chi square overall = 69.895304
p overall = 6.644e-16--------------------------------------------------------------------------------|      coef         se          z          p   lower CI   upper CI
-------------+------------------------------------------------------------------
hurdle       |                                                                  z_i |  3.644556   .4443773   8.201488   2.22e-16   2.773592   4.515519_cons | -1.727589   .1522467   -11.3473   7.65e-30  -2.025987  -1.429191
above        |                                                                  x_i |   .416768    .189209   2.202685   .0276169   .0459251   .7876109_cons |  .5702333   .1428997   3.990444   .0000659    .290155   .8503115
sigma        |                                                                  _cons |  1.053116   .0643765   16.35869          0   .9269402   1.179292
--------------------------------------------------------------------------------

Tobit 模型估计

的系数为 0.362 (在 10% 水平上显著) , 而 double hurdle 模型估计

的系数为 0.417 (在 5% 水平上显著), 由本次模拟结果来看 Tobit 估计似乎接近真实值 (

实际系数为 0.3), 但是双栏模型可以将决定

的变量

的系数估计出来 (估计为3.645), 非常接近真实值 4 (在 1% 水平上显著)。

[注：我们尝试通过设置不同的种子，生成不同的随机数，发现 double hurdle 模型对

的估计有时候会比 Tobit 模型估计更加准确]。

3. 面板双栏模型 (Panel-hurdle model)

3.1 面板双栏模型基本原理

Dong and Kaiser (2008) 将双栏模型发展成面板双栏模型，并使用这个模型对家庭牛奶消费做实证分析。Dong 假设并验证了家庭牛奶消费总的来说由非经济因素和经济因素决定，非经济因素包括户主年龄、教育、种族背景等，经济因素包括收入、牛奶的价格等。在一定的时间内，非经济因素一般不会发生改变，并且在家庭是否产生购买牛奶的行为中起决定性作用。

第一阶段 (first hurdle)

第二阶段 (second hurdle)

最终观测值

在第一个阶段中，

相当于非经济因素，

表示个体家庭是否会购买牛奶，基本不随着时间变化而改变；在第二个阶段中，

相当于经济因素，决定家庭购买牛奶的数量，

表示个体家庭潜在购买牛奶的数量，

代表个体效应, 且

与解释变量

均不相关。

表示个体家庭在第

期购买牛奶的数量。

似然函数模型

样本最终的似然对数函数为：

。

3.2 面板双栏模型的 Stata 实现

Stata 中用 xtdhreg 和 boothreg 命令对面板数据进行双栏模型的估计。首先在 Stata 命令窗口中输入 help xtdhreg 命令即可查看其完整帮助文件。xtdhreg 命令的基本语法为：

xtdhreg depvar indepvars [if] [in] [, up ptobit hd(varlist) uncorr trace ///difficult constraints(numlist)]

各项的含义如下：

depvar: 表示被解释变量，即最终的可观测的
indepvars：表示关键的解释变量，即决定
(潜变量) 的解释变量
up：将模型设置为右归并，并且设置
最大值（默认为左归并）
ptobit：将双栏模型设置为 p-tobit 模型
hd(varlist): 表示第一栏中决定
的解释变量
millr：用逆米尔斯比率来控制扰动项的相关性
uncorr：表示第一栏和第二栏中的扰动项不相关
trace：显示每一次迭代的系数
difficult：当模型不收敛时，换用其他替代的算法
constraints(numlist)：允许对模型进行限制

在 Stata 命令窗口中输入 help boothreg 命令即可查看其完整帮助文件。boothreg 命令的基本语法为：

bootreg depvar indepvars [if] [in] [, up ptobit hd(varlist) millr ///margins(string) seed(integer) reps(integer) strata(varlist) cluster(varlist) ///capt maxiter(integer)]

各项的含义如下：

depvar: 表示被解释变量，即最终的可观测的
indepvars：表示关键的解释变量，即决定
(潜变量) 的解释变量
up：将模型设置为右归并，并且设置
最大值（默认为左归并）
ptobit：将双栏模型设置为 p-tobit 模型
hd(varlist): 表示第一栏中决定
的解释变量
millr：用逆米尔斯比率来控制扰动项的相关性
margins(string)： bootstrep 估计的边际效应
seed(integer)：设置种子，为了使结果可重复
reps(integer)： boostrap 重复的次数，默认是 50 次
strata(varlist)：进行分层抽样
capt：自动忽略不收敛的情况
maxiter(integer)：设置迭代的最多次数，默认为 50

3.3 基于模拟分析的范例

本小节我们先模拟生成面板数据，然后再利用生成的数据进行模型估计。

数据生成过程 (DPG)

面板数据的个体为

, 一共有

期。这些个体的决策 (是否参与) 是由第一栏

是否大于 0 和第二栏

是否大于 0 共同决定的。值得注意的是,

不会随着时间

变化而改变，如果第一期

, 那么剩下的

期都会有

即该个体一直选择不参与；而当

时，

，个体暂时不参与但并不会影响其他几期该的决策。另外，我们设置了个体随机效应

, 并且

与第一个公式的误差项存在相关性。用 Stata 生成数据的过程如下：

clear all
set obs 2000
set seed 10011979
gen z_i = uniform()
set seed 1111122
gen u_i = rnormal(0, 3)
set seed 1222222
gen n_i = rnormal(0,3)
gen e_i1 = 0.9*u_i + sqrt(1-0.9^2)*n_i/* 面板数据生成过程 */
gen d_i = 0
replace d_i = 1 if -2 + 4*z_i + e_i1 > 0
gen id = _n
expand 5  // 将 T 设置为 5 期
bys id: gen t = _n
xtset id t
bysort id (t): gen x_it = rnormal(0,1) + rnormal(0,1) if _n==1
bysort id (t): replace x_it = .8 * x_it[_n-1] + rnormal(0,1) if _n!=1
gen e_i2 = rnormal(0,1)
gen y_it2 = 0.5 + 0.3*x_it + u_i + e_i2
corr e_i2 u_i // 检查e_i2和u_i的相关性
gen y_it1 = 0
replace  y_it1 = y_it2 if y_it2 > 0
gen y_it = y_it1*d_i
save data_process2.dta, replace  //保存模拟数据

模型估计 用 xtdhreg 命令进行双栏估计的结果如下：

use data_process2.dta, clear
help mdraws // 进行 xtdhreg 估计前，需要装`mdraws`包
xtdhreg y_it x_it, hd(z_i)
(output omitted)
Number of obs     =     10,000
Wald chi2(1)      =      46.82
Log likelihood = -9013.4217                     Prob > chi2       =     0.0000------------------------------------------------------------------------------Coef.   Std. Err.    z    P>|z|     [95% Conf. Interval]
----------------+-------------------------------------------------------------
hurdle          z_i |  .6908215   .1009566   6.84   0.000     .4929501    .8886929_cons | -.2702063   .0611108  -4.42   0.000    -.3899812   -.1504313
----------------+-------------------------------------------------------------
above           x_it |  .2971716   .0162833  18.25   0.000     .2652569    .3290863_cons |  3.887898   .1050517  37.01   0.000     3.682001    4.093796
----------------+-------------------------------------------------------------
sigma_u         _cons |  3.249278   .0942043  34.49   0.000     3.064641    3.433915
----------------+-------------------------------------------------------------
sigma_e         _cons |  .9920639    .012312  80.58   0.000     .9679329    1.016195
----------------+-------------------------------------------------------------
transformed_rho _cons | -.9211924   .0730788 -12.61   0.000    -1.064424   -.7779606
------------------------------------------------------------------------------rho:  tanh([transformed_rho]_cons)------------------------------------------------------------------------------|      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------rho |   -.726461   .0345118   -21.05   0.000    -.7941029   -.6588192
------------------------------------------------------------------------------separate Wald tests for joint significance of all explanatory variablesnoteif you use factor variables, i.e. the i., c., # and ## notation, you must runthe Wald test by hand. For detail see help fileestimates of joint significancechi square hurdle equation = 46.823275
p hurdle equation = 7.769e-12
chi square above equation = 333.06554
p above equation = 2.066e-74
chi square overall = 376.42223
p overall = 1.824e-82

用 bootdreg 命令进行双栏模型估计结果如下：

bootdhreg y_it x_it, hd(z_i)  cluster(id) capt
(output omitted)
maximum likelihood estimates of double hurdle modelN = 10000
log likelihood = -14962
chi square hurdle equation = 140.17438
p hurdle equation = 2.438e-32
chi square main equation = 140.17438
p main equation = 2.438e-32
chi square overall = 442.19897
p overall = 9.500e-97
bootstrap results------------------------------------------------------------------------------|      coef     se   p     lowciz      upciz     lowcip      upcip
------------+-----------------------------------------------------------------
hurdle      |                                                                 z_i |  1.002614   .122   0   .7634344   1.241794   .7598894   1.346414_cons | -.4531903   .072   0  -.5948118  -.3115688  -.6363495  -.2646514
main        |                    0                                            x_it |  .3388443   .052   0   .2370221   .4406664   .2289405   .4781399_cons |  2.279919   .132   0   2.020481   2.539356   1.868922   2.511813
sigma       |                                                                 _cons |  2.583072   .095   0   2.396594    2.76955   2.401081   2.808727
------------------------------------------------------------------------------

从回归结果可以看出，xtdhreg 和 bootdhreg 对样本的

系数估计值 (0.297 和 0.339) 非常接近

真实系数 (0.3)，且均在 1% 水平上显著。

参考文献

Bruno García, 2013, Implementation of a Double-Hurdle Model, Stata Journal, 13(4): 776–794. [pdf]
Christoph Engel, Peter G. Moffatt, 2014, Dhreg, Xtdhreg, and Bootdhreg: Commands to Implement Double-Hurdle Regression, Stata Journal, 14(4): 778–797. [pdf]
Dong, Diansheng, and H. M. Kaiser. Studying household purchasing and nonpurchasing behaviour for a frequently consumed commodity: two models[J]. Applied Economics, 2008, 40(15):1941-1951. [PDF]
Engel C, Moffatt P G. Dhreg, xtdhreg, and bootdhreg: Commands to implement double-hurdle regression[J]. Stata Journal, 2014, 14(4):778-797. [PDF]

相关课程

连享会-直播课 上线了！ http://lianxh.duanshu.com 免费公开课：

直击面板数据模型 - 连玉君，时长：1 小时 40 分钟
Stata 33 讲 - 连玉君, 每讲 15 分钟.
部分直播课 课程资料下载 (PPT，dofiles 等)

Note: 助教招聘信息请进入「课程主页」查看。

因果推断-内生性专题 ⌚ 2020.11.12-15
主讲：王存同 (中央财经大学)；司继春(上海对外经贸大学) 课程主页： https://gitee.com/arlionn/YG | 微信版

空间计量专题 ⌚ 2020.12.10-13
主讲：杨海生 (中山大学)；范巧 (兰州大学) 课程主页： https://gitee.com/arlionn/SP | 微信版

关于我们

Stata 连享会 由中山大学连玉君老师团队创办，定期分享实证分析经验。直播间 有很多视频课程，可以随时观看。
连享会-主页 和 知乎专栏，300+ 推文，实证分析不再抓狂。
公众号推文分类：计量专题 | 分类推文 | 资源工具。推文分成 内生性 | 空间计量 | 时序面板 | 结果输出 | 交乘调节 五类，主流方法介绍一目了然：DID, RDD, IV, GMM, FE, Probit 等。