Laplacian on Triangle Mesh

Laplacian on Triangle Mesh

局部平均区域

基本思想是mesh面上的点x的值设置为其局部领域的平均。下图是几种具体的情况：

其中蓝色区域为局部平均区域。

1. Barycentric cell：三角形的重心和三角形边的中点相连
2. Voronoi cell：三角形的外心和三角形的中点相连（对于钝角三角形可能会出现外心在外部）
3. Mixed Voronoi cell：在Voronoi cell的基础上，将钝角三角形的外心替换成钝角对边的中点

梯度

拉普拉斯算子是梯度的散度，所以我们需要先求出梯度。

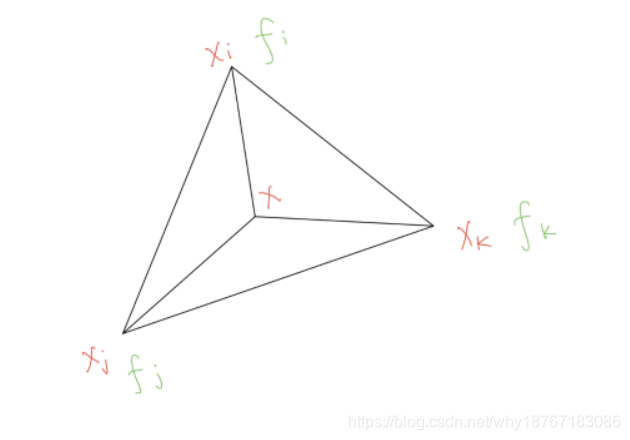
属性插值函数：
$$f(x)=\alpha f_i+\beta f_j+\gamma f_k$$
其中：$f_i,f_j,f_k$是三角形三个顶点的属性值，x为三角形内部的点，$\alpha ,\beta ,\gamma$ 是点x在三角形的重心坐标，$\alpha +\beta +\gamma =1$。

梯度：
$${\nabla }_{x}f(x)=f_i{\nabla }_x\alpha +f_j{\nabla }_x\beta +f_k{\nabla }_x\gamma$$
对于$\alpha$来说：
$$\alpha =\frac{A_i}{A_T}=\frac{((x-x_j)\cdot \frac{(x_k-x_j{)}^{\perp }}{||x_k-x_j|{|}_2})||x_k-x_j|{|}_2}{2A_T}=\frac{(x-x_j)\cdot (x_k-x_j{)}^{\perp }}{2A_T}$$
对$x$求导：
$$\begin{gathered} {\nabla }_x\alpha =\frac{(x_k-x_j{)}^{\perp }}{2A_T} \\ {\nabla }_x\beta =\frac{(x_i-x_k{)}^{\perp }}{2A_T} \\ {\nabla }_x\gamma =\frac{(x_j-x_i{)}^{\perp }}{2A_T} \end{gathered}$$
得到梯度公式：
$${\nabla }_{x}f(x)=f_i\frac{(x_k-x_j{)}^{\perp }}{2A_T}+f_j\frac{(x_i-x_k{)}^{\perp }}{2A_T}+f_k\frac{(x_j-x_i{)}^{\perp }}{2A_T}$$
因为
$$(x_k-x_j{)}^{\perp }+(x_i-x_k{)}^{\perp }+(x_j-x_i{)}^{\perp }=0$$
所以
$${\nabla }_{x}f(x)=(f_j-f_i)\frac{(x_i-x_k{)}^{\perp }}{2A_T}+(f_k-f_i)\frac{(x_j-x_i{)}^{\perp }}{2A_T}$$

离散拉普拉斯算子

均匀拉普拉斯

$$\Delta f(v_i)=\frac{1}{|N_1(v_i)|}\sum _{v_j\in N_1(v_i)}(f_j-f_i)$$

此公式可以用于各向同性的remesh上。

余切形式的拉普拉斯

使用混合的有限元/有限体方法（mixed finite element/finite volume method），拉普拉斯算子可以更加精确地进行离散推导。目标是在局部平均区域A_i=A(v_i)上，对逐片线性函数梯度地散度进行积分。

$${\int }_{A_i}\Delta fdA={\int }_{A_i}div\nabla fdA={\int }_{\partial A_i}(\nabla f)\cdot nds$$
将积分分解到每个三角形上，并且局部的Voronoi区域通过三角形两条边的中点$a$和$b$，并且每个三角形中$\nabla f(x)$是常数，那么在该三角形$T$上的积分为
$${\int }_{\partial A_i\cap T}\nabla f\cdot nds=\nabla f\cdot (a-b{)}^{\perp }=\frac{1}{2}\nabla f(u)\cdot (x_j-x_k{)}^{\perp }$$

将梯度公式代入：
$${\int }_{\partial A_i\cap T}\nabla f\cdot nds=(f_j-f_i)\frac{(x_i-x_k{)}^{\perp }\cdot (x_j-x_k{)}^{\perp }}{2A_T}+(f_k-f_i)\frac{(x_j-x_i{)}^{\perp }\cdot (x_j-x_k{)}^{\perp }}{2A_T}$$

因为
$$A_T=\frac{1}{2}sin{\gamma }_j||x_j-x_i||||x_j-x_k||=\frac{1}{2}sin{\gamma }_k||x_i-x_k||||x_j-x_k||$$

$$\begin{gathered} cos{\gamma }_j=\frac{(x_j-x_k)\cdot (x_j-x_k)}{||x_j-x_i||||x_j-x_k||} \\ cos{\gamma }_k=\frac{(x_i-x_k)\cdot (x_j-x_k)}{||x_i-x_k||||x_j-x_k||} \end{gathered}$$

于是得到：
$${\int }_{\partial A_i\cap T}\nabla f\cdot nds=\frac{1}{2}(cot{\gamma }_k(f_j-f_i)+cot{\gamma }_j(f_k-f_i))$$
在整个局部平均区域$A_i$上积分得到：
$${\int }_{\partial A_i\cap T}\nabla f\cdot nds=\frac{1}{2}\sum _{j\in \Omega (i)}(cot{\alpha }_{ij}+cot{\beta }_{ij})(f_j-f_i)$$
所以在顶点$v_i$处，函数$f$的拉普拉斯算子的离散平均为：
$$\Delta f(v_i)=\frac{1}{2A_i}\sum _{j\in \Omega (i)}(cot{\alpha }_{ij}+cot{\beta }_{ij})(f_j-f_i)$$

矩阵化求解拉普拉斯

$$\Delta f(v_i)=w_i\sum _{v_j\in {\mathcal{N}}_1(v_i)}{w}_{ij}(f(v_j)-f(v_i))$$
其中$w_i=\frac{1}{2A_i},w_{ij}=cot{\alpha }_{ij}+cot{\beta }_{ij}$。将线性和写成矩阵形式：
$$\left(\begin{array}{c}\Delta f(v_1)\\ ⋮\\ \Delta f(v_n)\end{array}\right)=\underset{L}{\underbrace{DM}}\left(\begin{array}{c}f(v_1)\\ ⋮\\ f(v_n)\end{array}\right)$$
其中$D=diag(w_1,...,w_n)$，M是对称矩阵：
$$m_{i,j}=\{\begin{array}{ll}-{\sum }_{v_k\in {\mathcal{N}}_1(v_i)}{w}_{ik},& i=j\\ w_{ij},& v_j\in {\mathcal{N}}_i(v_i)\\ 0,& \text{otherwise}\end{array}$$
更高阶的拉普拉斯可以递归得到：
$${\Delta }^{k}f(v_i)=w_i\sum _{v_j\in {\mathcal{N}}_1(v_i)}{w}_{ij}({\Delta }^{k-1}f(v_j)-{\Delta }^{k-1}f(v_i))$$
那么这个矩阵表示就很简单的对应拉普拉斯矩阵$L$的$k$次幂$L^k=(DM{)}^k$。

因此在n个顶点的mesh上更高阶的偏微分方程${\Delta }^{k}f=b$离散化之后会得到一个$(n\times n)$的线性系统：
$$L^{k}x=b$$
其中$x=(f(v_1),...,f(v_n){)}^T$，且$b=((b(v_1),...,b(v_n)){)}^T$

矩阵性质

稀疏性 简单说一下吧。拉普拉斯矩阵中只有对角元和边对应的元素是非0的，其余全是0。根据欧拉公式，平均每一行大约7个非0元素。

对称性 由于对角矩阵$D$捣乱，所以矩阵$L=DM$不是对称的。不过对于任意k阶的拉普拉斯系统很容易转换为对称系统，即
$$M(DM{)}^{k-1}x=D^{-1}b$$
正定性 一般来讲，解偏微分方程都需要边界条件。即对于一个线性系统$Ax=b$，有部分变量$x_i$保持不变，此时它们不再是未知量了。此时将对应的列$a_i$移到右手边，即$b\leftarrow b-x_i{a}_i$，同时对应的行从整个系统中移除。注意到此时整个系统还是保持对称的！！！在移除边界条件之后，可以证明矩阵$L$是负定的！负定很简单，直接在每个$L$上乘一个-1就行，因此我们最后得到
$$(-1{)}^{k}M(DM{)}^{k-1}x=(-1{)}^k{D}^{-1}b$$
由此我们就得到了一个稀疏、对称且正定的线性系统。

Reference

[1]http://staff.ustc.edu.cn/~fuxm/course/2019_Spring_DGP/index.html
[2]https://optsolution.github.io/archives/19907.html