本文主要是介绍长短时期记忆（LSTM）及门控循环单元（GRU）网络结构，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
一、背景
1、RNN自身可以通过不停的将信息循环操作，保证信息持续存在，从而可以利用前面得事件信息来对后面得事件进行分类操作。
2、RNN处理这类任务时不一定就可以完全得理解之前的记忆，因为在语句过长得情况下，之前的文本内容在传到后期时已经不再具有那么的信息。
（1）在‘the clouds are in the sky’中，如果最后进行预测，则我们可以大概率的将sky进行预测出来。
（2）若在一个复杂的任务中‘I grew up in France… I speak fluent French.’如果在这句话中我们要进行最后一个单词French的预测就比较麻烦，因为我们最后一个单词离France比较远。
3、在RNN中若要解决2的（2）这类问题则需要通过调参的操作来进行解决。
二、LSTM网络
1、标准的RNN与LSTM网络的对比
（1）在RNN中每个重复的模块仅具有比较简单的一个网络结构
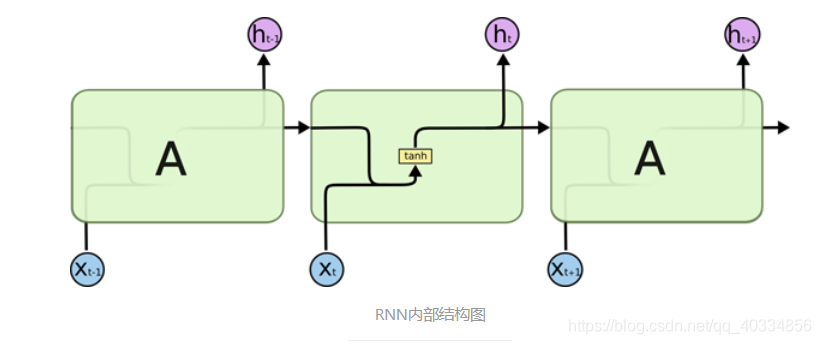
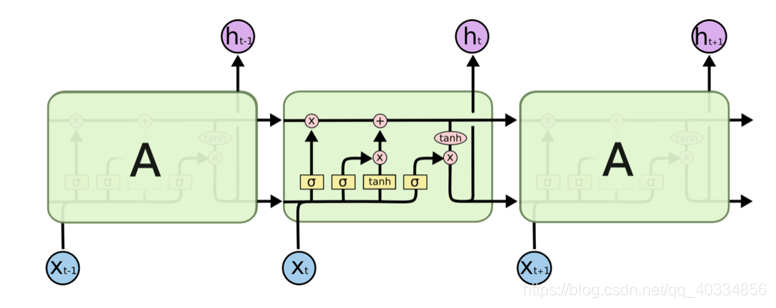
（2）在LSTM中，它与RNN具有类似的这种链式结构，区别于RNN的地方在于，它的内部具有四个复杂的网络层。
以下为LSTM中各类符号的定义图
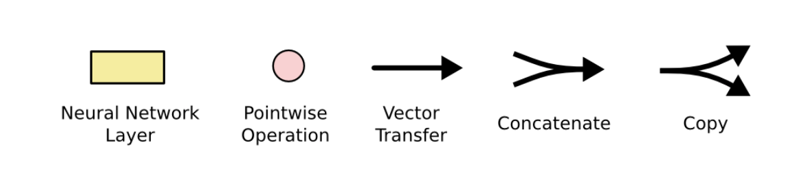
图中黄色类似于CNN里的激活函数操作，粉色圆圈表示点操作，单箭头表示数据流向，箭头合并表示向量的合并（concat）操作，箭头分叉表示向量的拷贝操作。
2、简述LSTM的核心内容
我们可以把LSTM的核心理解为一个细胞状态，用贯穿细胞的水平线进行表示。这个细胞状态和一个传送带类似，它虽然贯穿整个细胞，却仅有很少的分支出现，只有这样才能保证信息可以不变的流过整个循环神经网络（RNN）。
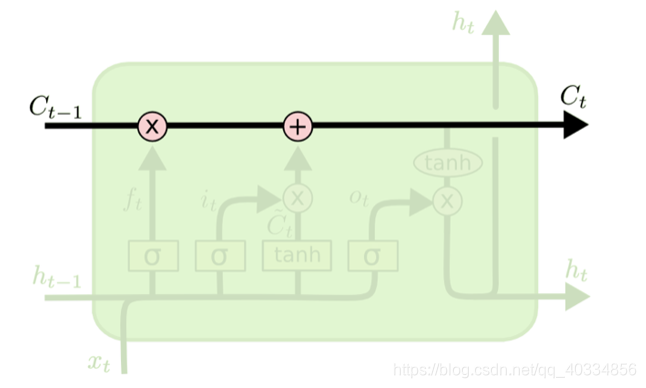
然而，在LSTM的网络中，我们可以通过一种被称为门的结构，对细胞状态中的信息进行删除或者添加信息。
这些门可以选择性的决定让细胞状态中的哪些信息通过；门的结构也很简单，在LSTM的内部，门的结构为一个sigmoid层和一个点乘操作的组合。
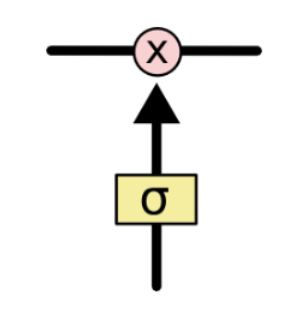
由于sigmoid层的输出值是在0到1之间，这代表着有多少的信息可以流过sigmoid层。通常0表示都不能通过，而1表示都能通过。
通常在一个LSTM中包含三个门来控制细胞状态
3、一个一个门的打开LSTM（遗忘门、输入门、输出门）
（1）遗忘门
LSTM的第一件事情是需要决定我们的细胞状态需要丢弃哪些信息。所以我们通过遗忘门来进行这项操作，这个遗忘门是通过sigmoid的单元来进行处理操作的。它通过查看 h t − 1 h_{t-1} ht−1和 x t x_t xt中的信息来输出一个0-1之间的向量，该向量里面的0-1值可以表示细胞状态 C t − 1 C_{t-1} Ct−1中的哪些信息保留或丢弃多少。0表示不保留，1表示保留。遗忘门的结构如下图。
f t = σ ( W f ∗ [ h t − 1 , x t ] + b f ) f_t = \sigma(W_f*[h_{t-1},x_t]+b_f) ft=σ(Wf∗[ht−1,xt]+bf)
（2）输入门
通过输入门，我们可以决定为当前的细胞状态添加哪些新的信息。这一步分为两个子步骤，第一步，我们得利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过一个称为输入门的操作来决定更新哪些信息。第二步，利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过一个tanh层得到新的候选细胞信息 C T ′ C'_T CT
这篇关于长短时期记忆（LSTM）及门控循环单元（GRU）网络结构的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
