密码学安全性证明（二）Identity-Based Encryption from the Weil Pairing

2023-10-11 02:20

文章标签 安全性证明 based 密码学 identity encryption pairing weil

本文主要是介绍密码学安全性证明（二）Identity-Based Encryption from the Weil Pairing，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

IND-ID-CCA:
在这里插入图片描述 IND-CPA:

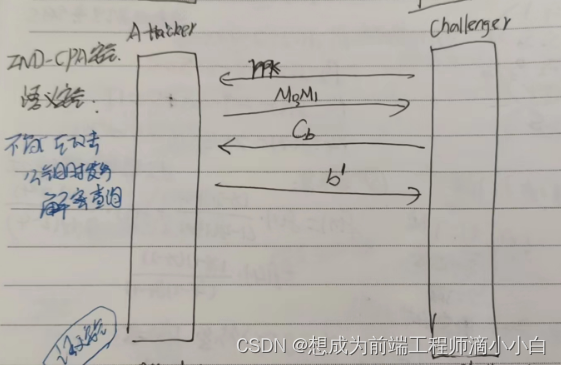
IND-ID-CPA:
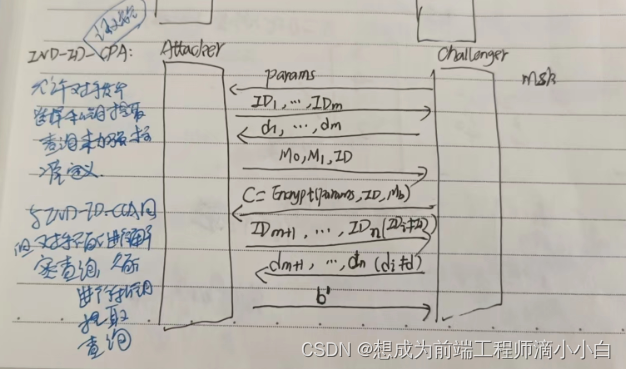BasicIdent:

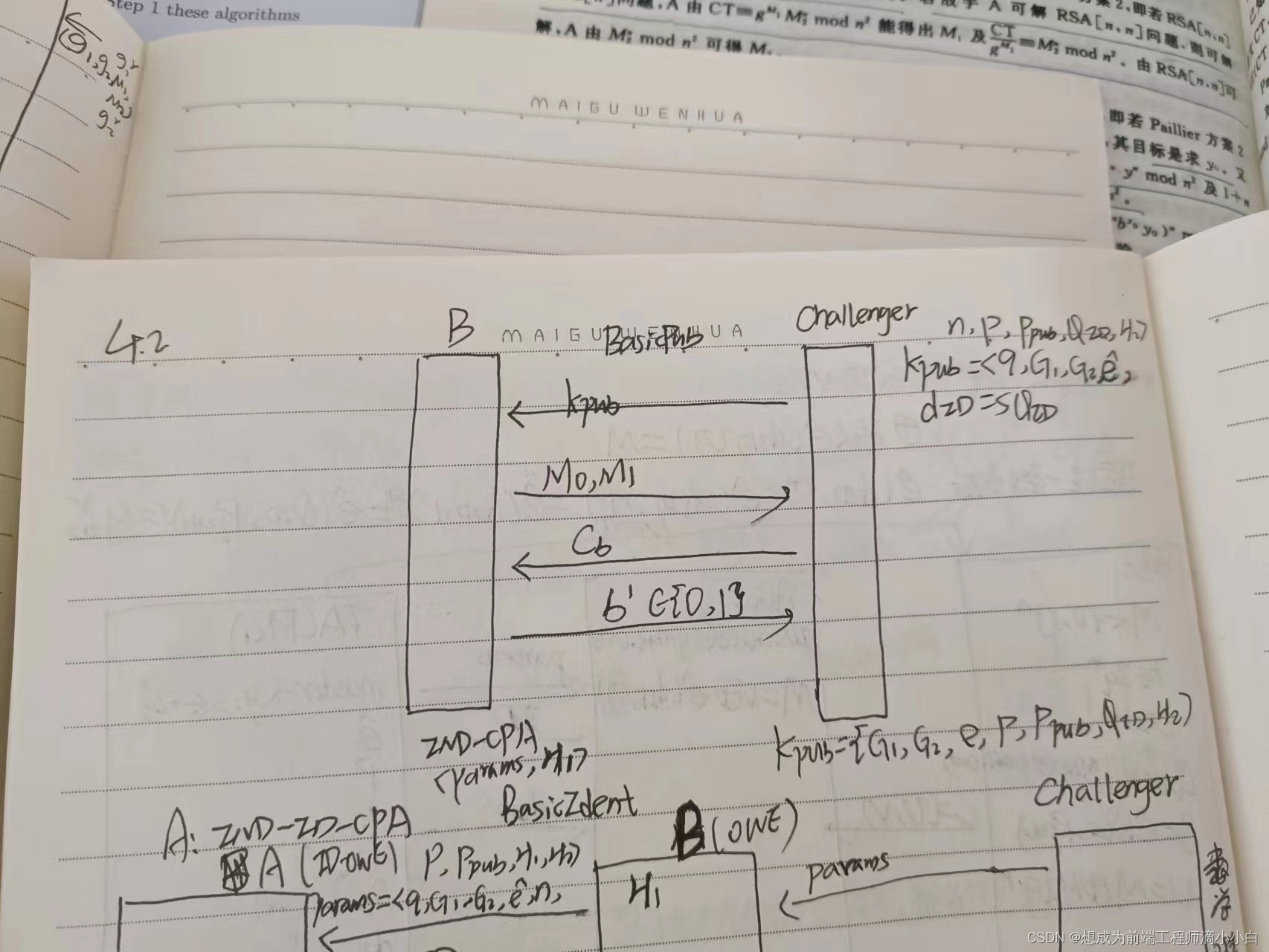
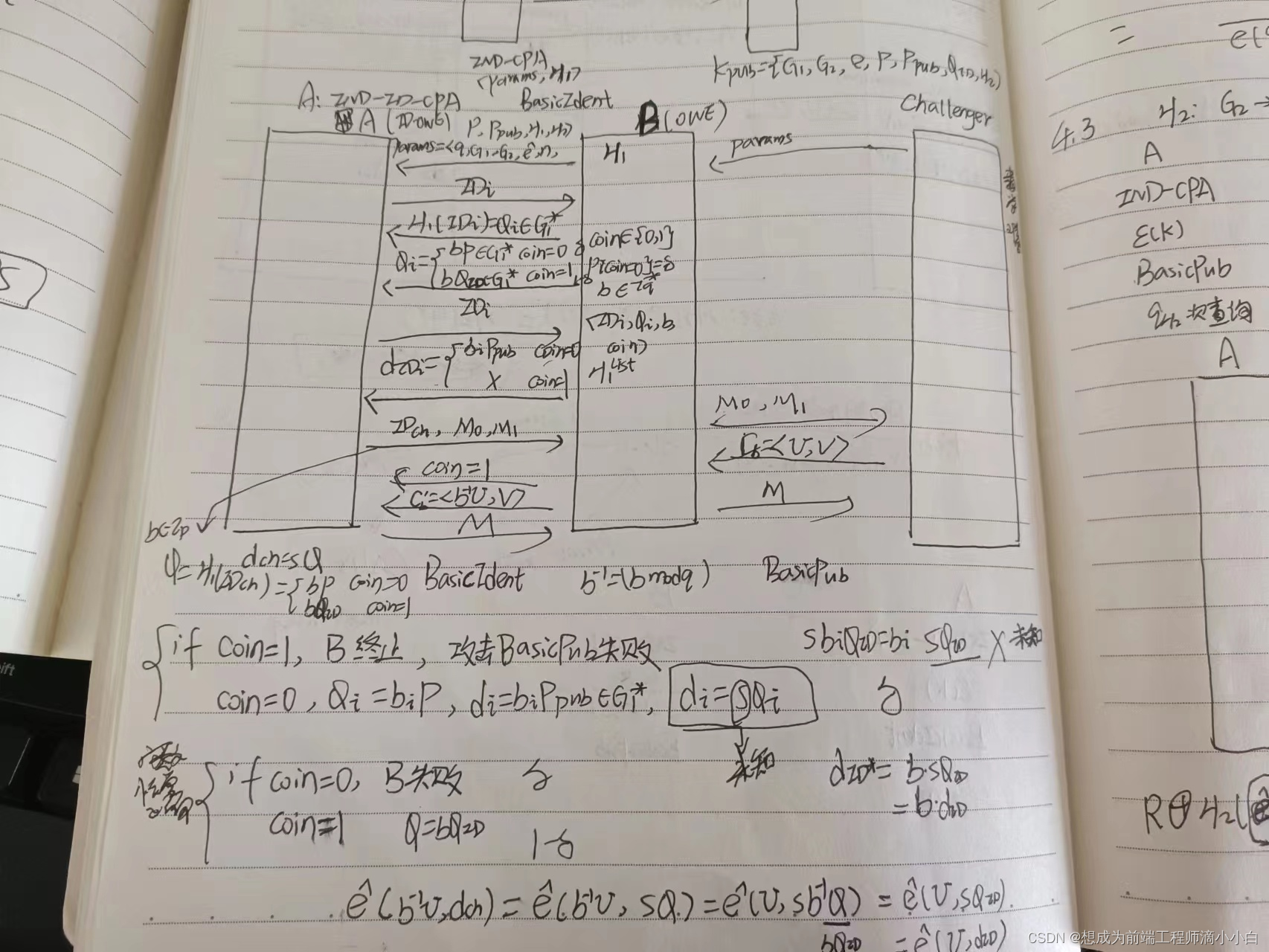
在这里插入图片描述

这篇关于密码学安全性证明（二）Identity-Based Encryption from the Weil Pairing的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/184817。 23002807@qq.com

Retrieval-based-Voice-Conversion-WebUI模型构建指南

一、模型介绍 Retrieval-based-Voice-Conversion-WebUI（简称 RVC）模型是一个基于 VITS（Variational Inference with adversarial learning for end-to-end Text-to-Speech）的简单易用的语音转换框架。具有以下特点简单易用：RVC 模型通过简单易用的网页界面，使得用户无需深入了

如何用百度网盘开关远程桌面3389端口增强安全性

密码学读书笔记小结

密码学是保证消息的私密性和完整性以及消息认证的基础。加密算法的选择和密钥的管理是安全机制的效率、性能和可用性的关键。公钥加密算法：分发密钥比较容易，但是对大数据量的加密性能较差密钥加密算法：更适合大批的加密任务混合型加密协议：例如TLS，先用公钥加密建立一个安全通道，然后使用通道交换密钥，并将此密钥用于后续数据交换。对分布式系统攻击的分类：窃听：未经授权获得消息副本伪装：在未

MACS bdgdiff: Differential peak detection based on paired four bedGraph files.

参考原文地址：[http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html](http://manpages.ubuntu.com/manpages/xenial/man1/macs2_bdgdiff.1.html) 文章目录一、MACS bdgdiff 简介DESCRIPTION 二、用法

Neighborhood Homophily-based Graph Convolutional Network

#paper/ccfB 推荐指数： #paper/⭐ #pp/图结构学习流程重定义同配性指标： N H i k = ∣ N ( i , k , c m a x ) ∣ ∣ N ( i , k ) ∣ with c m a x = arg ⁡ max ⁡ c ∈ [ 1 , C ] ∣ N ( i , k , c ) ∣ NH_i^k=\frac{|\mathcal{N}(i,k,c_{

国产隔离放大器：增强信号完整性和系统安全性的指南

隔离放大器是电子领域的关键组件，特别是在信号完整性和电气隔离至关重要的应用中。这些放大器隔离输入和输出信号，使它们能够在没有直接电气连接的情况下跨不同系统传输数据。这确保了电路一部分的高压尖峰或噪声不会影响另一部分，从而保护了系统和用户。随着国产隔离放大器的不断发展，它们提供了性能、可靠性和成本效益的完美结合，使其成为工程师和系统设计师的理想选择。 1. 了解国产隔离放大器的优势增强信号

NISP | 密码学

关注这个证书的其他相关笔记：NISP 一级 —— 考证笔记合集-CSDN博客通过上一章的学习，我们知道了，网络安全的 CIA 模型，而本期学习的“密码学”，则能为 CIA 模型提供很好的技术支持：面临的攻击威胁所破坏的信息安全属性解决问题所采用的密码学技术截获（泄露信息）机密性对称密码和非对称密码篡改（修改信息）完整性哈希函数、数字签名、对称密码和非对称密码伪造（伪造信息来源）真实

Android Studio打开Modem模块出现：The project ‘***‘ is not a Gradle-based project

花了挺长时间处理该问题，特记录如下：1.背景：在Android studio 下导入一个新增的modem模块，如MPSS.DE.3.1.1\modem_proc\AAA, 目的是看代码方便一些，可以自由搜索各种关键字。但导入该项目时出现了如下错误： The project '***' is not a Gradle-based project.造成的问题： (1) project 下没有代码，而

SIM(Search-based user interest modeling)

导读我们对电商场景兴趣建模的理解愈发清晰：1. 通过预估目标item的信息对用户过去的行为做search提取和item相关的信息是一个很核心有效的技术。2. 更长的用户行为序列信息对CTR建模是非常有效且珍贵的。从用户的角度思考，我们也希望能关注用户长期的兴趣。但是当前的search方法无论是DIN和DIEN都不允许我们在线对一个超长的行为序列比如1000以上做有效搜索。所以我们的目标就比较明

一种极简的余弦定理证明方法

余弦定理的证明方法有很多种，这里介绍一种极简的证明方法。该方法是本人在工作中推导公式，无意中发现的。证明非常简单，下面简单做下记录。如上图为任意三角形ABC，以点C为原点，建立直角坐标系（x轴方向任意，y轴与x轴垂直），x轴与CB夹角为 θ 1 \theta_1 θ1，x轴与CA夹角为 θ 2 \theta_2 θ2。点B的坐标为 ( a c o s θ 1 , a s i n θ

密码学安全性证明（二）Identity-Based Encryption from the Weil Pairing

相关文章