分支界定算法实践(三) 精确求解TSP

TSP问题是非常经典的NP难问题，问题描述很简单，但是求解难度却很大。首先还是给出TSP的数学描述：

• 图$G(V,E)$是一个无向简单图，集合$V$包含了顶点$1,2,...,n$，集合$E$包含了所有边$e(i,j),i,j\in V$. 每条边$e(i,j)$都有对应的权重$w_{ij}\ge 0$. 需要找到一个边集合$T\subset E$，其包含的边构成了图的最短路径，最短路径的长度可以定义为${\sum }_{(i,j)\in T}{w}_{ij}$，图上的每对顶点$s,t\in V$都存在只属于$T$的边来相通，并且每个顶点都只有两个属于$T$的边被确定

一般会把TSP问题用01变量或者置换队列来进行数学描述, 如果是01变量的表述形式，通用的分支界定算法也可以求解，不过我们可以使用一些更加特异化的分支界定算法，更具效率，本文就介绍其中一种

分支界定是一种求精确解的算法，如果TSP的顶点数太多，无论多高明的分支界定算法也无能为力，所以它只适用于规模较小的情况。分支界定算法只是一种算法框架，要应用该算法，需要首先从整体上确定算法中的三个主要成分的实现手段，然后具体细化所有的算法步骤。这三个算法主要成分是：

• 分支策略：我们需要决定如何对父结点进行分支，也就是添加新约束来产生子问题结点；
• 定界策略：在每个问题结点上，需要求解当前约束下的问题下界，同时整个算法也维护一个问题上界，如果该问题的下界大于上界，那么该结点可以进行剪枝；
• 分支结点选择：对于多个可以进行分支的结点，我们也需要用一种选择策略选取结点进行分支

下面我们具体分析. 首先需要确定的是如何表述TSP问题和约束，也就是决策变量是哪个。这里我们明确决策变量是所有边的状态，如果边$e_{ij}=1$，表示该边在路径上(included edge)；如果$e_{ij}=0$，表示该边不在路径上(excluded edge)，这样求解TSP的过程可以看作是从图中选取边来构成一条最短的路径。

确定分支策略。每一次产生子问题，就是在父问题的图中选择一条尚未确定状态的边来设定状态，加入路径或者排除出路径。在根节点，所有的边都没有确定状态，随着分支过程的进行，越来越多的边的状态被确定，最终达到一些可行解。在选择边的具体实现上，有两种方式：

• 按照字典序选边(Lexicographic Order, LG)。这是比较简单直接的方式，例如在当前结点，边$e_{1,2}$被加入路径，对其进行分支，那么按照字典序就选择边$e_{1,3}$，如果边$e_{1,3}$已经被确定了状态，那就继续看边$e_{1,4}$，以此类推
• 按照边长升序选择(Increasing Length, IL)。就是说选择剩余未明确边中最小长度的边，这种选取方式基于思想是选取更小的边加入路径，更有可能较早地找到最短路径

而在通过分支加入新的边约束之后，一些额外的边状态检查和确定工作也需要被执行，来达到一种类似"约束传播"的效果，减小搜索空间：

• 如果某个顶点上除了两条相邻边，都被排除出了路径，那么这两条边肯定要被加入路径
• 如果某个顶点上已经有两条加入路径的相邻边，那么所有其他的相邻边都要被排除出路径
• 对于一条未确定状态的边，如果把它加入路径会导致子回路产生，那么这条边一定要被排除出路径

接着确定定界策略。全局上界很明显就是当前的最短路径，每次找到一个更短的全路径，就用这个值更新上界；而在每个子问题结点上，如何计算下界是需要着重讨论的。在分支界定算法中，在每个结点上的最优解的目标值是肯定不会比下界更小的，在TSP问题中，下界就是当前结点对应的图中最短路径所能达到的理论最小值(所谓理论，就是除了已经确定好的边，其他未确定状态边可以任意设定状态)。同样我们也有两种计算下界的方法：

• 简单下界(Simple lower bound, SB)。对每个顶点$i$，假设$(a_i,i)$和$(b_i,i)$是顶点$i$的两个相邻边，这两条边要么是已经明确在路径中的，要么是未确定状态边中最短的，那么下界就是所有顶点的这两条边长的总和：
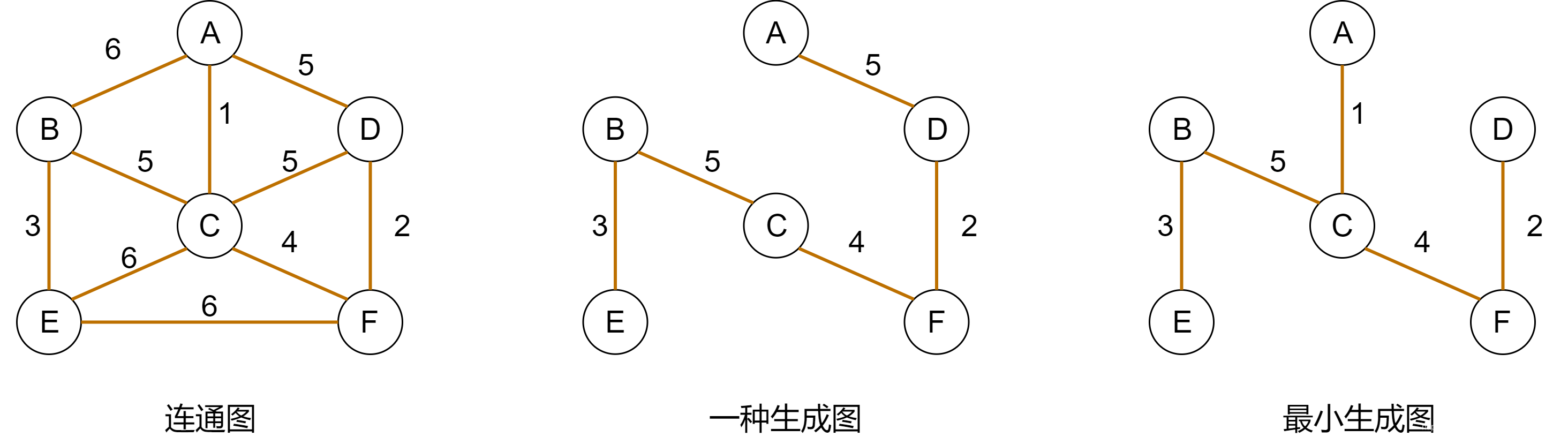
  $$L=\frac{1}{2}\sum _{i=1}^n{w}_{a_{i}i}+w_{b_{i}i}$$
• 1-tree下界(OT)。1-tree是最小生成树的变体，首先生成树指的是指一个连通图的子图，它含有图中全部$n$个顶点，但只有足以构成一棵树的$n-1$条边，如果生成树中再添加一条边，则必定成环；所有生成树中边权重和最小的叫最小生成树(MST)，下图是生成树和最短生成树的示意图：
  
  在最小生成图的基础上，我们这样定义1-tree：图$G(V,E)$是全连接无向图，1-tree是指顶点 { 2 , . . . , n } \{2,...,n\} {2,...,n}加上顶点1及顶点1两条相邻边构成的生成树，总权重最小的1-tree则是最小1-tree。最小1-tree可以通过顶点 { 2 , . . . , n } \{2,...,n\} {2,...,n}的MST加上顶点1的两条最短边构成，下图是一个最小1-tree的示意图
  

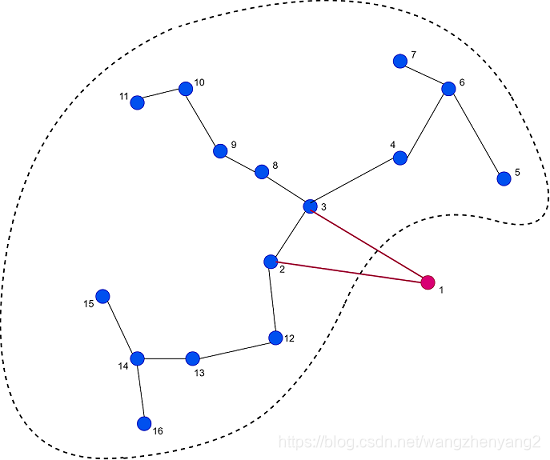
回到TSP问题，可以用最小1-tree的值来作为下界值，1-tree里的顶点1就是TSP的起点。

最后是分支结点的选择。我们对于最小化问题，一般都会采取更小下界优先的原则，也就是先选下界更小的结点来分支，因为这样找到一个更短路径的可能性更大一些，也就意味着尽可能早的更新全局上界，这样后续分支时也更可能剪枝，提升算法速度。对TSP问题，我们采用同样的策略。

下面用python代码实现一个TSP实例，采用IL+SB策略组合的分支界定算法。首先给出一个距离矩阵作为问题实例，这是一个numpy二维数组，尺寸是14X14，也就是14个顶点：

size=14
costs=np.array([ [0,  141,  118,  171,  126,  69,   158, 79, 166, 208, 65, 67, 98, 97],[141,  0,  266,   34,  212,  208,  82, 114, 305, 324, 165, 75, 187, 118],[118, 266, 0, 232, 56, 107, 194, 109, 229, 122, 61, 151, 60, 201],[171, 34, 232, 0, 200, 233, 63, 128, 332, 347, 188, 104, 180, 146],[126, 212, 56, 200, 0, 105, 145, 84, 228, 170, 55, 123, 19, 181],[69, 208, 107, 233, 105, 0, 212, 113, 123, 144, 54, 133, 96, 163],[158, 82, 194, 63, 145, 212, 0, 104, 324, 323, 161, 93, 137, 161],[79, 114, 109, 128, 84, 113, 104, 0, 236, 225, 65, 51, 58, 133],[166, 305, 229, 332, 228, 123, 324, 236, 0, 187, 177, 230, 219, 239],[208, 324, 122, 347, 170, 144, 323, 225, 187, 0, 165, 249, 198, 298],[65, 165, 61, 188, 55, 54, 161, 65, 177, 165, 0, 91, 48, 140],[67, 75, 151, 104, 123, 133, 93, 51, 230, 249, 91, 0, 104, 73],[98, 187, 60, 180, 19, 96, 137, 58, 219, 198, 48, 104, 0, 161],[97, 118, 201, 146, 181, 163, 161, 133, 239, 298, 140, 73, 161, 0] ])

定义Node类，代表分支界定的每个结点。Node类包含名为constraints的属性，它是二维数组，其元素表示了各条边的状态，为0表示该边排除出路径，为1表示该边加入路径，为2表示该边的状态尚未确定

import math
import copy
import numpy as npclass Node:def __init__ (self, size , costs ,sortedEdges ,allSortedEdges ,parent_constr , extra_constr = None):self.size = size self.costs = costs self.sortedEdges = sortedEdgesself.allSortedEdges = allSortedEdgesself.extra_constr = extra_constrself.constraints = self.determine_constr(parent_constr)self.lowerBound = self.computeLowerBound()def computeLowerBound(self):'''计算当前结点的下界, 采用the simple lower bound(SB)的方式,即所有顶点的两个最小可行临边的和'''lb = 0for i in range(self.size):lower = 0t = 0for j in range(self.size):if self.constraints[i][j] == 1:lower += self.costs[i][j]t += 1tt = 0while t < 2:shortest = self.sortedEdges[i][tt]if self.constraints[i][shortest] == 2:lower += self.costs[i][shortest]t += 1tt += 1if tt >= self.size:lower = math.infbreaklb += lowerreturn lbdef determine_constr(self,parent_constr):'''在父结点的基础上加入分支约束来构成当前结点的边约束'''constraints = copy.deepcopy(parent_constr)if self.extra_constr == None:return constraintsfr = self.extra_constr[0]to = self.extra_constr[1]constraints[fr][to] = self.extra_constr[2]constraints[to][fr] = self.extra_constr[2]for i in range(2):constraints = self.removeEdges(constraints)constraints = self.addEdges(constraints)return constraintsdef removeEdges(self,constraints):'''对于当前结点, 去除掉所有不可行边(Excluding edges):1) 如果某个顶点已经有两条相邻边是Including edges, 那么其余相邻边排除2) 如果加入这条边会导致子回路产生, 该边排除'''for i in range(self.size):t = 0for j in range(self.size):if (i != j) and (constraints[i][j] == 1):t += 1if t >= 2:for j in range(self.size):if constraints[i][j] == 2:constraints[i][j] = 0constraints[j][i] = 0# 检测任意的i和j之间是否存在回路可能, 如果从j可以从边l(i,j)外的边回溯到i, 那么边l(i,j)要被排除for i in range(self.size):for j in range(self.size):t = 1prev = ifr = jcycle = FalsenextOne = self.next_one(prev ,fr,constraints)while (nextOne[0]):t += 1next = nextOne[1]if next == i:cycle = Truebreakif t > self.size:breakprev = frfr = nextnextOne = self.next_one(prev ,fr,constraints)if (cycle) and (t < self.size) and (constraints[i][j] == 2):constraints[i][j] = 0constraints[j][i] = 0return constraintsdef addEdges(self,constraints):'''对于当前结点下的每个顶点, 如果它的相邻边只剩两条没有被排除, 那么这两条边肯定要被包含'''for i in range(self.size):t = 0for j in range(self.size):if constraints[i][j] == 0:t += 1if t == self.size-2:for j in range(self.size):if constraints[i][j] == 2:constraints[i][j] = 1constraints[j][i] = 1return constraintsdef next_one(self,prev ,fr,constraints):'''从顶点prev到顶点fr, 检测是否存在第三个顶点到fr, 如果没有, 返回false如果有, 返回true, 并返回这第三个顶点'''for j in range(self.size):if (constraints[fr][j] == 1) and (j != prev):return [True ,j]return [False]def isTour(self):'''检测当前结点是否是一个全路径: 如果一个图的每个顶点都只有两个相邻边, 其他相邻边都被排除, 那么该图是一个全路径'''for i in range(self.size):num_zero = 0num_one = 0for j in range(self.size):if self.constraints[i][j] == 0:num_zero += 1elif self.constraints[i][j] == 1:num_one += 1if (num_zero != self.size-2) or (num_one != 2):return Falsereturn Truedef contains_subtour(self):'''检测当前结点的图中是否存在子回路:对每个顶点, 检测是否存在长度小于顶点数的回溯路线'''for i in range(self.size):next = self.next_one(i,i,self.constraints)if next[0]:prev = ifr = next[1]t = 1next = self.next_one(prev , fr, self.constraints)while next[0]:t += 1prev = frfr = next[1]if (fr == i) and (t < self.size):return Truenext = self.next_one(prev ,fr,self.constraints)if t == self.size:return Falsereturn Falsedef tourLength(self):'''返回全路径时的路径长度'''length = 0fr = 0to = self.next_one(fr,fr,self.constraints)[1]for i in range(self.size):length += self.costs[fr][to]temp = frfr = toto = self.next_one(temp ,to,self.constraints)[1]return lengthdef next_constraint(self):'''决定用于下一次分支的边, 使用IL方法'''for edge in self.allSortedEdges:i = edge[0]j = edge[1]if self.constraints[i][j] == 2:return edgedef __str__ (self):if self.isTour():result = '0'fr = 0to = Nonefor j in range(self.size):if self.constraints[fr][j] == 1:to = jresult += '-' + str(j)breakfor i in range(self.size-1):for j in range(self.size):if (self.constraints[to][j] == 1) and (j != fr):result += '-' + str(j)fr = toto = jbreakreturn resultelse:print('This node is not a tour')

定义TSP类，作为算法的主类。在构造方法中初始化IL和SB所需的数据结构，在findSolution中递归调用BranchAndBound方法进行分支界定算法计算

from Node import Node
import math
import time
import copyclass TSP:def __init__(self,size ,costs ,bestTour = math.inf):self.size = sizeself.costs = costsself.bestTour = bestTourself.bestNode = Noneself.bestNodeTime = 0self.num_createdNodes = 0self.num_prunedNodes = 0self.sortedEdges = self.sort_edges()self.allSortedEdges = self.sort_allEdges()def findSolution(self):root = self.create_root()self.num_createdNodes += 1T1 = time.perf_counter()self.BranchAndBound(root)T2 = time.perf_counter()print('---------------------------------------------------------------------')print('The shortest tour is:', self.bestNode)print('It has a length of', self.bestTour , 'km')print('Found in',T2 - T1, 'seconds')print('Best tour was found after:',self.bestNodeTime ,'seconds')print('Number of nodes created:',self.num_createdNodes)print('Number of nodes pruned:',self.num_prunedNodes)def sort_edges(self):'''对距离矩阵每行进行升序排序result的每行表示第i个顶点, 每行上的元素是其他顶点号码, 按距离升序排列'''result = []for i in range(self.size):result.append([x for (y, x) in sorted(zip(self.costs[i],list(range(self.size))))])return resultdef sort_allEdges(self):'''所有边按边长升序排列'''edges = []lengths = []for i in range(self.size):for j in range(i + 1, self.size):edges.append([i, j])lengths.append(self.costs[i][j])result = [z for (l, z) in sorted(zip(lengths , edges))]return resultdef create_root(self):'''root结点, 没有任何边约束'''no_constraints = []for i in range(self.size):row_i = []for j in range(self.size):if (i != j):row_i.append(2)else:row_i.append(0)no_constraints.append(row_i)root = Node(self.size ,self.costs ,self.sortedEdges ,self.allSortedEdges ,no_constraints)return rootdef BranchAndBound(self,node):if node.isTour():if node.tourLength() < self.bestTour:self.bestTour = node.tourLength()self.bestNode = nodeself.bestNodeTime = time.perf_counter()print('Found better tour:', self.bestNode ,'of length',self.bestTour , 'km')else:new_constraint = copy.copy(node.next_constraint())new_constraint.append(1) # 左节点上包含这条边leftChild = Node(self.size ,self.costs ,self.sortedEdges ,self.allSortedEdges ,node.constraints , new_constraint)new_constraint[2] = 0 # 右节点上排除这条边rightChild = Node(self.size ,self.costs ,self.sortedEdges,self.allSortedEdges ,node.constraints , new_constraint)self.num_createdNodes += 2if self.num_createdNodes % 401 == 0:print('Number of nodes created so far:', self.num_createdNodes)print('Number of nodes pruned so far:', self.num_prunedNodes)if self.num_createdNodes % 51 == 0:print('.')if (leftChild.contains_subtour()) or (leftChild.lowerBound > 2 * self.bestTour):leftChild = Noneself.num_prunedNodes += 1if (rightChild.contains_subtour()) or (rightChild.lowerBound > 2 * self.bestTour):rightChild = Noneself.num_prunedNodes += 1if (leftChild != None) and (rightChild == None):self.BranchAndBound(leftChild)elif (leftChild == None) and (rightChild != None):self.BranchAndBound(rightChild)elif (leftChild != None) and (rightChild != None):if leftChild.lowerBound <= rightChild.lowerBound:self.BranchAndBound(leftChild)self.BranchAndBound(rightChild)else:self.BranchAndBound(rightChild)self.BranchAndBound(leftChild)

在主程序中用如下的代码进行测试：

from Node import Node
from TSP import TSP
import numpy as npsize=14
costs=np.array([ [0,  141,  118,  171,  126,  69,   158, 79, 166, 208, 65, 67, 98, 97],[141,  0,  266,   34,  212,  208,  82, 114, 305, 324, 165, 75, 187, 118],[118, 266, 0, 232, 56, 107, 194, 109, 229, 122, 61, 151, 60, 201],[171, 34, 232, 0, 200, 233, 63, 128, 332, 347, 188, 104, 180, 146],[126, 212, 56, 200, 0, 105, 145, 84, 228, 170, 55, 123, 19, 181],[69, 208, 107, 233, 105, 0, 212, 113, 123, 144, 54, 133, 96, 163],[158, 82, 194, 63, 145, 212, 0, 104, 324, 323, 161, 93, 137, 161],[79, 114, 109, 128, 84, 113, 104, 0, 236, 225, 65, 51, 58, 133],[166, 305, 229, 332, 228, 123, 324, 236, 0, 187, 177, 230, 219, 239],[208, 324, 122, 347, 170, 144, 323, 225, 187, 0, 165, 249, 198, 298],[65, 165, 61, 188, 55, 54, 161, 65, 177, 165, 0, 91, 48, 140],[67, 75, 151, 104, 123, 133, 93, 51, 230, 249, 91, 0, 104, 73],[98, 187, 60, 180, 19, 96, 137, 58, 219, 198, 48, 104, 0, 161],[97, 118, 201, 146, 181, 163, 161, 133, 239, 298, 140, 73, 161, 0] ])tsp=TSP(size,costs)
tsp.findSolution()

计算结果:

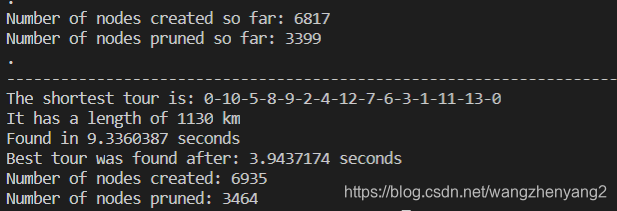
同时可以用下面的代码来测试一下暴力搜索法的效果，下面的暴力搜索把顶点数减少到10个，但计算时间已经远大于分支界定算法

from Node import Node
from TSP import TSP
import numpy as np
import itertools
import math
import timesize=10
costs=np.array([ [0,  141,  118,  171,  126,  69,   158, 79, 166, 208, 65, 67, 98, 97],[141,  0,  266,   34,  212,  208,  82, 114, 305, 324, 165, 75, 187, 118],[118, 266, 0, 232, 56, 107, 194, 109, 229, 122, 61, 151, 60, 201],[171, 34, 232, 0, 200, 233, 63, 128, 332, 347, 188, 104, 180, 146],[126, 212, 56, 200, 0, 105, 145, 84, 228, 170, 55, 123, 19, 181],[69, 208, 107, 233, 105, 0, 212, 113, 123, 144, 54, 133, 96, 163],[158, 82, 194, 63, 145, 212, 0, 104, 324, 323, 161, 93, 137, 161],[79, 114, 109, 128, 84, 113, 104, 0, 236, 225, 65, 51, 58, 133],[166, 305, 229, 332, 228, 123, 324, 236, 0, 187, 177, 230, 219, 239],[208, 324, 122, 347, 170, 144, 323, 225, 187, 0, 165, 249, 198, 298],[65, 165, 61, 188, 55, 54, 161, 65, 177, 165, 0, 91, 48, 140],[67, 75, 151, 104, 123, 133, 93, 51, 230, 249, 91, 0, 104, 73],[98, 187, 60, 180, 19, 96, 137, 58, 219, 198, 48, 104, 0, 161],[97, 118, 201, 146, 181, 163, 161, 133, 239, 298, 140, 73, 161, 0] ])#tsp=TSP(size,costs)
#tsp.findSolution()minLength = math.inf
minTour = []
T1 = time.perf_counter()
for tour in itertools.permutations(list(range(1,size))):fr = 0length = 0count = 0while count < size-1:to = tour[count]length += costs[fr][to]fr = tocount += 1length += costs[fr][0]print('New tour :', tour)if length < minLength:minLength = lengthminTour = tour
minTour = (0,) + minTour + (0,)
T2 = time.perf_counter()
print('Shortest tour is:', minTour)
print('It has a length of:', minLength , 'km')
print('Found in',T2 - T1, 'seconds')