关于《Harnessing Deep Neural Networks with Logic Rules》对规则融入神经网络的理解

阅读感想：最近在总结关于规则怎么与神经网络相结合，所以阅读了ACL16的这篇文章。这篇文章是规则融入神经网络的一篇经典文章，其他关于规则与神经网络结合的文章的思想与这篇并无太大区别，只是具体实现方式不同。

问题背景：数据驱动的深度学习方法给人工智能的各个方向带来了巨大的变化，但这种方法依赖大量的标签数据且具有可解释性差、难训练等问题。事实上，人类的行为表明，人类的学习不仅来源于具体的例子，还来源于不同形式的通用知识和丰富的经验。逻辑规则体现着人类交流过程中的高水平认知和结构化知识，将规则融入神经网络对于学习过程有着巨大的帮助。

方法概述：作者提出的方法借助模型蒸馏的概念，提出了通过对Student Network和Teacher Network进行迭代训练，在每一次迭代过程，通过对Student Network进行规则正则化子空间的映射得到Teacher Network。最后根据Teacher Network的输出和student Network的输出对Student Network进行反向更新。如下图所示，整个方法详细描述将会围绕着几个公式展开。

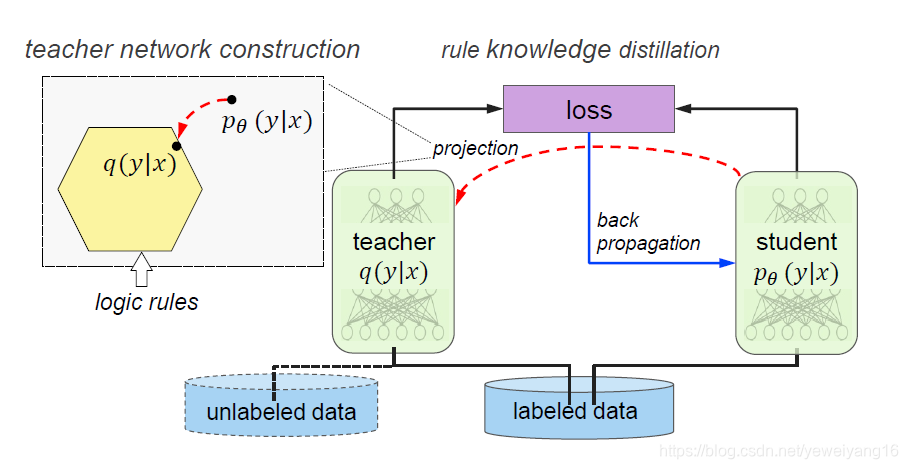
 构造Teacher Network：

首先在Teacher Network中，使用时软逻辑来编码encode一阶逻辑规则，软逻辑是在连续区间[0, 1]中取值的，这样的好处在于增加了灵活性并且方便后面的优化。

Teacher Network的概率分布 每次迭代是从Student Network的概率分布。作者在这里对构造出来的Teacher Network有两点要求：（1）Teacher Network的概率分布q要尽量与student Network的概率分布p相近。（2）Teacher Network的分布要尽量满足规则。第一条约束我们可以使用KL散度来实现，第二条是通过松弛因子来的，其中松弛因子又是根据每条规则的置信度（表明该条规则的重要程度）和实例满足程度（期望算子）来决定的。最后给出如下公式：

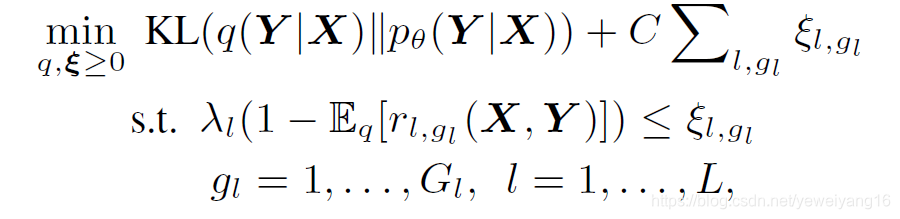
因为这是一个凸优化的问题，所以使用对偶形式可以得到如下解：

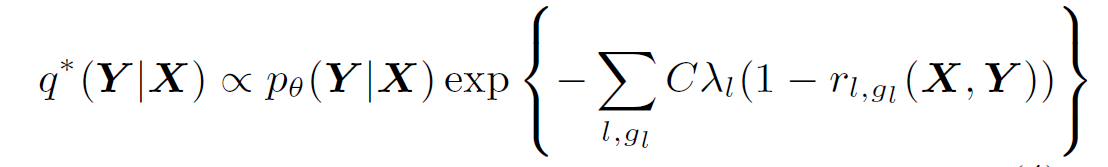
知识蒸馏：这部分的结果就是想通过平衡teacher network的输出和student network的输出以及真实标签来获得更新student network的参数。它的目标函数是：

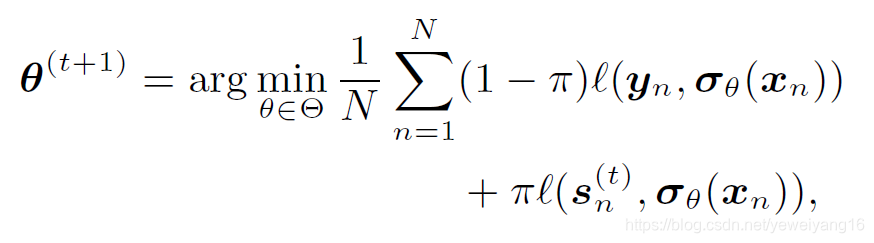
其中是调节参数，控制两个网络的偏向程度，损失函数用的交叉熵损失，前面的是student网络，后面的是teacher网络。在原文中，作者还提到一个问题，为什么不先把teacher network构造好，而是要采用迭代的方式同时训练？作者给出了两点原因：（1）使用迭代蒸馏的方式可以获得更好的表现。（2）我们使用参数而不是显示的规则表达，这样就可以在测试阶段预测新样例的时候如果规则不可取或者获取代价过大，那么依旧可以获取良好的表现。

实验流程：

最后的测试阶段，我们对teacher network和student network都进行了测试，实验表明，两者相对于base line都有显著的提高，通常来说，teacher的表现要比student好。特别的，teacher适合逻辑规则覆盖大量样本的事情，student更加轻量级和高效率，适合在预测时，逻辑规则获取困难和位置的情况。