本文主要是介绍SHA384-算法解密(2)还原元数据,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
SHA384-算法解密(2)还原元数据
上一次的讲解比较潦草,这次写的更全面详细一些。
首先各位,如果想要解开使用这个算法加密后的数据,必须先学会加密,才能解密。
声明:这里仅供学习研究,不要学了三脚猫功夫就去惹麻烦
适用于HTTPS/HTTP ,SOCKET 传输的变量需要加密
apk,web,webGame 都适用 短变量类型
不适用 文本.超文本.大文件
1. 什么是SHA384
SHA是哈希混淆散列,散列算法又称杂凑算法或哈希算法,能将一定长度的消息计算出固定长度的字符串(也可以叫摘要算法)。SHA包含5个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384和SHA-512,后四者并称为SHA-2。
我个人观察评判,且各个行业使用优先的排列:
sha256->sba384->sha512->sha1
SHA-384最大计算明文长度为2^128bit,属于分组算法,分组长度为1024bit,产生的信息摘要长度为384bit。SHA-384算法属于密码杂凑算法,原则上不能通过密文推出明文。
2. 组成元 \符 \号
- 一组数据为一元或一单元
- 一符 为一转义,偏移,单步
- 一号 为一运算,公式,组合
| 效果 | 元 | 符 | 号 |
|---|---|---|---|
| <<<1<<k | gfedcbah | abcdefgh | m |
| h[k]=h[k]+h<<<[1] | h0~h7 | m’ | |
| mod | |||
| s0 s1 | |||
| w[i] | |||
| ∧ | |||
| ∨ | |||
| ⊕ | |||
| >>>k | |||
| >>k | |||
| ← | |||
| ~ | |||
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
h0~h7:8个64bit双字,初始哈希值,也存放每组计算的当前哈希值
abcdefgh:8个64bit双字,存放中间变量
m:消息
m':填充后的消息
mod:模运算
s0,s1:字节扩展时中间变量
S0,S1,ch,maj,temp1,temp2:循环迭代时中间变量
w[i]:第i个扩展双字
∧:64bit与运算
∨:64bit或运算
⊕:异或运算
>>>k:循环右移k比特运算
>>k:右移k比特运算
←:左向赋值运算符
~:64bit双字按位取反
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||_|_|D|I|A|B|L|O|
<<<1<<k :1是元 k是符, 向左偏移了1位 得出的1,就是元数据了。
为什么叫 元?
现在输入一个字符串:
abc
填充后消息:
0x61 0x62 0x63 0x80 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x18
————————————————————————————————
这里不是主要讲解去理解怎么加密的,而是带入一下话题,好让大家整理一下思路;
这里主要是做解密,所以要懂一些基础的原理。现在我们大概知道了元符号是怎么回事啦;
然后看一下这组数据有什么规律,或无规律?
要加密的数值为 50

这套算法其实是有漏洞可寻的,某些大厂的加密解密委托我测试研究;
不论你使用的工具也好,还是在线脚本,或者自己编写一个工具编写生成。
他都会有变动,不是100%的固定值。
公式是 ([生成端]时间+[被生成]数据)+虚拟混淆段
更像是 VMP虚拟壳一样,把数值虚拟化了,要从虚拟化的数据中找到真正的值,在解开;
搞过破解的都知道VMP,让不少crack头疼,我也其中之一 哈哈哈!。。。最后还是解开
你任何时间都可以测试,比如早上9.00整 加密一个数值,你多次的加密是一个值,但9.01就变了一个值。也可能到10点前都不变动,随机性很大。所以摸清楚一个元符号的规律要花几个星期不等的时间。
没有必要的数值,最好不要浪费时间!
当我把我的惊奇发现公布了以后,不少人DISS我,怎么可能,你有那么厉害吗?
我这里澄清一下,我是蒙的,一蒙就对了!真的!
蒙一个对了,蒙个3,5个都对吗?是的!就是对了!!
话归正传
从上面的十六进制里,完全看不出什么规律。过一段时间,在生成一个50的加密数据出来
放入UE里,以十六进制编辑模式打开
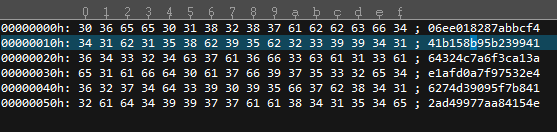
此时,发现头步的 04变成了06,结尾的e没有变化。
我们把公式拿过来拆解一下,看看有什么发现没有。

h= g
g= f
f= e
e= d + temp1
d= c
c= b
b= a
a= temp1 + temp2
赋值初始哈希值a= h0
b= h1
c= h2
d= h3
e= h4
f= h5
g= h6
h= h7
只需要关注十六进制你要找出的值,其余都是虚拟,障眼法!会干扰你的思路。
你在代入公式的时候,不妨把h看做0,即为0x00= 00;
那按照这个假设06= h6对吧?h6=g,g=f,那最后f一步一步偏移回到h;
如果你学过编程,那么这种赋值方式,f=e g=f,原有的数值还是在的,只是重新排列而已?
我们看一下50的十六进制是多少。

那么变化成元就是= cec0 在变成赋值的初始哈希
h2h4h2h0 然后把这个初始哈希 找出来。
初始哈希值:
h0=0xcbbb9d5dc1059ed8,
h1=0x629a292a367cd507,
h2=0x9159015a3070dd17,
h3=0x152fecd8f70e5939,
h4=0x67332667ffc00b31,
h5=0x8eb44a8768581511,
h6=0xdb0c2e0d64f98fa7,
h7=0x47b5481dbefa4fa4
我们这里用代码演示啦!
var temp=["0x9159015a3070dd17", //把它扔进数组变量里
"0x67332667ffc00b31",
"0x9159015a3070dd17",
"0xcbbb9d5dc1059ed8"];//这里迭代 80次
for(i from 0 to 79){S1= (e >>> 14) ⊕ (e >>> 18) ⊕ (e >>> 41)ch= (e∧ f) ⊕ ((~ e) ∧ g)temp1= h + S1 + ch + k[i] + w[i]S0= (a >>> 28) ⊕ (a >>> 34) ⊕ (a >>> 39)maj= (a∧b) ⊕ (a∧c)⊕(b∧c)temp2= S0 + maj
}
h= g
g= f
f= e
e= d + temp1
d= c
c= b
b= a
a= temp1 + temp2大概的加密算法,可能不完整,但我主要不是研究写加密,是教大家怎么解开!不要DISS我
temp1= h + S1 + ch + k[i] + w[i]
就是说 第一次运算出的值,是总值,总值再做一次运算
那么来推导一次;
h=9159015a3070dd1767332667ffc00b319159015a3070dd170xcbbb9d5dc1059ed8,
S1=字节扩展时的中间变量,ch=循环迭代时中间变量;
字节变量= 0000000000000000000000000000000000000000000000006162638000000000
循环变量=470994ad30873f88086c5b2d36a89178470994ad30873f88470994ad30873f88
k[3][5]][3][0]=e9b5dba58189dbbc59f111f1b605d019e9b5dba58189dbbc428a2f98d728ae22
这样庞大计算力,显然不是人力能够计算的,就算依靠计算机的运算,没有百年,也解不开。
那怎么计算呢?
还记得刚才我说的 比对两个文件十六进制吗?
把刚才推导得出的答案 元cec0 转换为初始值 9159015a3070dd1767332667ffc00b319159015a3070dd17cbbb9d5dc1059ed8
把他扔进UE 以十六进制编辑查看

元数值是没有偏移的,所以偏移4位看看,b和a 发现了35 30?我们把他们反转一下在看

此时我们已经加密解密SHA384 -成功!
但这有些投机取巧,如果数值在庞大一些怎么计算?
怎么保证每次都成功?
如果不知道原数值怎么计算呢?
我只公布一小段,代表这套算法已经能被破解了,其它的算法也一样。
我是一个游戏前端,只是喜欢研究花里胡哨的东西
越是说的厉害邪乎的东西,我越想破解
哪个公司能收我?

我是大菠萝,欢迎各位切磋技术
有疑问或者问题尽管提问,或者PK一下
这篇关于SHA384-算法解密(2)还原元数据的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




