计算机博弈 基本算法 极大极小算法

计算机博弈大赛中最基础的算法就是极大极小算法，下面总结MaxMin算法

预备知识：
广度优先搜索(BFS)
深度优先搜索(DFS)

介绍

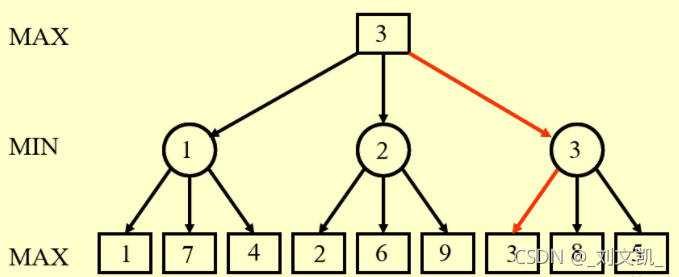
MaxMin算法在有限深度的范围内进行搜索，假定博弈双方都是聪明的，也就是每次都会选择可能获胜的最大值。那么对于我方来说，对方每次都会选取使我方获胜的最小值MIN；我方会选择使我方获胜的最大值MAX。
“值”的数字，由最后一层状态的评估函数f§确定，评估函数。
定义：
MAX与MIN分别代表博弈双方。
p代表一个棋局状态
f§表示评估函数
过程：
当父状态为MIN时，那么子层将最小值传上去，如果父状态为MAX是，将子层的最大值传上去。

实现

广度优先实现：

深度优先实现：

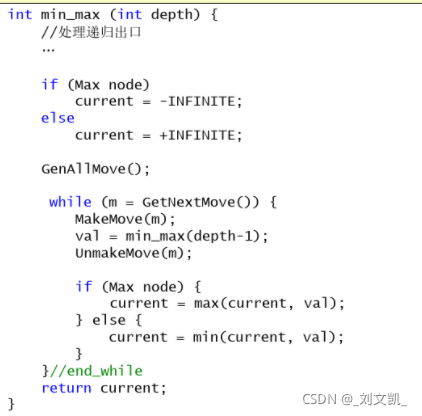
评估函数：
评估函数的确定根据，博弈的种类不同而不同，以简单的“井字棋”为例，评估函数可以是当前状态p我方胜利的线条数减去对方胜利的线条数：

f(p) = number(max)-number(min)

一般而言最终的状态应当是博弈双方进行了相同的步骤，如深度为3层5层。