分布滞后模型与自回归模型

分布滞后模型与自回归模型

第一节 滞后效应与滞后变量模型

一、经济活动中的滞后现象

一般说来，解释变量（自变量）对被解释变量（因变量）的影响不可能在短时间内完成，在这一过程通常存在时间滞后，也就是说，解释变量需要通过一段时间才能完全作用于被解释变量，所研究的解释变量存在着滞后项。此外，由于经济活动的惯性，一个经济指标以前的变化态势往往会延续到本期，从而形成被解释变量的当期变化同自身过去取值水平相关的情形。这种被解释变量受自身或其他经济变量过去值影响的现象称为滞后效应。
常见有滞后效应例子有消费滞后、通货膨胀滞后。

二、滞后效应产生的原因

1. 心理预期因素
   由于人们的心理定势及社会习惯的作用，适应新经济条件和经济环境需要一个过程，从而表现为决策滞后。例如，人们预期价格上涨时，会加快当期商品的购买。
2. 技术因素
   在国民经济运行中，从生产到流通再到使用，每一个环节都需要一段时间，从而形成时滞。最经典例子就是农产品产量对价格信息的反应总是滞后的，原因在于农产品的生产需要一个较长的时间过程。
3. 制度因素
   契约、管理制度等因素也会形成一定程度的滞后。

三、滞后变量模型

滞后变量是指过去时期的、对当前被解释变量产生影响的变量。它可分为滞后解释变量与滞后被解释变量。将滞后变量引入回归模型，这种模型就叫做滞后变量模型。一般采用此模型，就将经济活动的静态分析转化为动态分析。

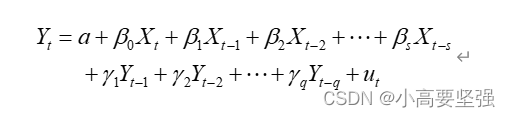
式子中，s、q分别是滞后解释变量与滞后被解释变量的滞后长度，若滞后长度为有限，则称该模型为有限滞后变量模型；若滞后长度为无限，则称模型为无限滞后模型。

1. 分布滞后模型
   如果滞后模型中没有滞后被解释变量，即形式为下式：
   

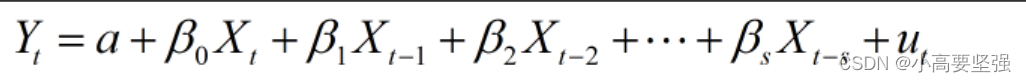
我们根据滞后长度s取值的有限和无限，划分有限分布滞后模型和无限分布滞后模型。
B0称为短期乘数或即期乘数，表示本期各时期X变动一个的单位对Y值的影响。Bi(i=1,2,3…,s)，表示过去各时期X变动一个单位对Y值的影响；

2. 自回归模型
   如果滞后变量模型的解释变量仅包含自变量X的当期值和被解释变量的若干期滞后值，模型的形式为
   
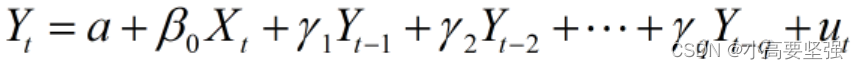
   式子中，q为自回归模型的阶数，称这类模型为自回归模型。

第二节 分布滞后模型的估计

一、分布滞后模型估计的困难

有学者认为用被解释变量分别对解释变量（包括滞后项）进行逐步回归，直到滞后变量的回归系数开始变成统计上不显著或至少有一个变量的系数改变符号时候结束。
但这样有如下缺陷：

1. 自由度问题
   随着滞后长度s的增加，有效样本容量n-s变小，会出现自由度不足的问题。
2. 多重共线性问题
   由于经济活动的前后继起性，经济变量的滞后值之间通常存在较强的联系，因此，分布滞后模型中滞后解释变量观测值之间会存在严重的多重共线性问题。
3. 滞后长度难以确定
   模型中滞后长度的确定较为困难。对于滞后长度难以确定这一问题，除可以用模型变量设定误差检验意外，如果缺乏先验信息，可以选择AIC或SIC等模型选择准则来确定，可选择能使AIC或SIC最小的滞后长度。

对于有限滞后模型，其基本思想是对滞后模型中的系数施加某种约束，以减少需要估计模型参数的个数，以缓解多重共线性，保证自由度。对于无限分布滞后模型，主要是通过适当的模型变换，使其转换为只需估计有限个参数的自回归模型。有限分布滞后模型的常用估计方法主要有经验加权估计法、阿尔蒙法等。

二、经验加权估计法

所谓经验加权估计法，就是根据实际经济问题的特点及经验判断，对解释变量的系数赋予一定的权数，利用这些权数构成的各滞后变量的线性组合，以形成新的变量，再应用最小二乘法进行估计。权数分布的确定取决于模型滞后结构的不同类型，常见的滞后结构类型如下：

1. 递减滞后结构
   这类滞后结构假设权数是递减的，认为滞后解释变量对被解释变量的影响随着时间的推移越来越小。
2. 不变滞后结构
   这类滞后结构假定权数不变，即认为滞后解释变量对被解释变量的影响不随着时间变化而变化。
3. ^形滞后结构
   两头小中间大的结构，这类滞后结构适合用于前后期滞后解释变量对被解释变量影响不大，但中期影响较大的分布滞后模型。

例如，假设某个经济变量服从一个滞后3期的分布滞后模型：

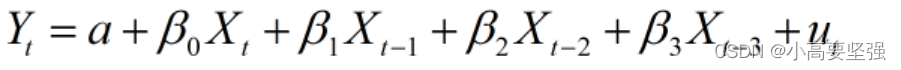
如果根据经验判断滞后变量对被解释变量的影响递减，权数取某种形式，如1/2、1/4、1/6、1/8，则有

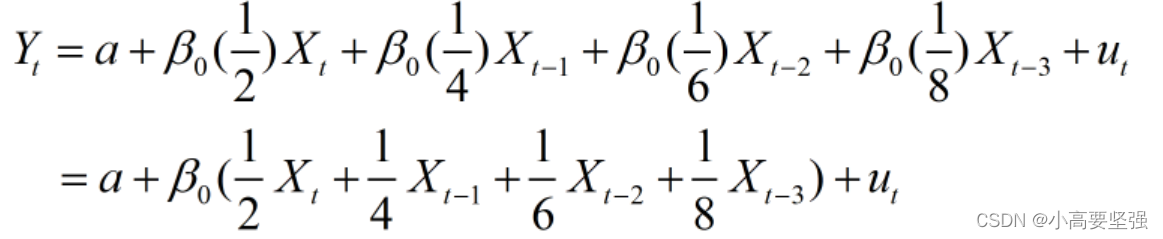
令新的线性组合变量为：

原模型就变为经验加权模型为：

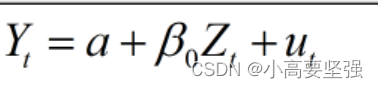
若随机扰动项与解释变量不相关，则与滞后解释变量的线性组合变量也不相关，因此我们可以用最小二乘法对该模型进行估计，从而得出原来模型各个解释变量的系数。

经验加权估计法具有简单易行、少损失自由度、避免多重共线性干扰等特点，且参数估计具有一致性。缺点是设置权数的主观随意性较大，要求分析者对实际问题的特征有比较透彻的了解。通常做法是根据先验信息，多选择几组权数，然后根据可决系数、F检验值等选出最佳估计方程。

三、阿尔蒙法

阿尔蒙法是利用多项式来逼近滞后参数的变化结构，从而减少待估参数的数目。其基本原理是，在有限分布滞后模型滞后长度s已知的情况下（重点条件），滞后系数可以看作相应滞后期i的函数，我们用一个关于i的次数较低的m次多项式很好地逼近滞后参数，即：

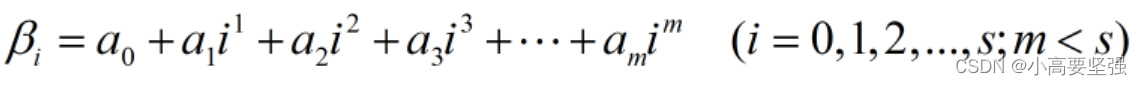
最后，可以整理得出：

这样，在随机扰动项满足古典假定的条件下，可用最小二乘法进行估计，求出各个a值，就可以推算出Bi的系数。
在实际应用中，阿尔蒙多项式的次数m通常取得很低，一般取2或3，很少超过4。我们可以看出通过阿尔蒙变换，新模型的变量个数少于原分布滞后模型中变量个数，从而自由度得到保证，并在一定程度上缓解了多重共线性问题。

第三节 自回归模型的构建

在下面所讲解的模型中，都会有每个模型特定的假设，在特定假设条件下，构建特定的模型。

一、库伊克模型

在考虑建立有限分布滞后模型来分析时，则存在滞后长度难以确定的问题。为了回避这一难点，可以使用无限分布滞后模型来处理。
但是，无限分布滞后模型中滞后项无限多，而样本观测总是有限的，因此不可能对其直接进行估计。显然，要使模型估计能够顺利进行，必须是假一些约束或假设条件，将模型的结构作某种变换。
库伊克变换假定：滞后解释变量Xt-i对被解释变量Y的影响随着滞后期i（i=0,1,2,…）的增加而按几何级数衰减，即滞后系数的衰减服从某种公比小于1的几何级数：

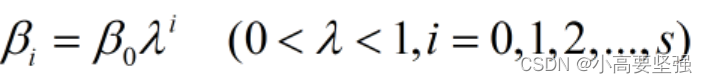
式子中，B0为常数，公比为待估参数。

将Bi代入无限分布滞后模型中得：

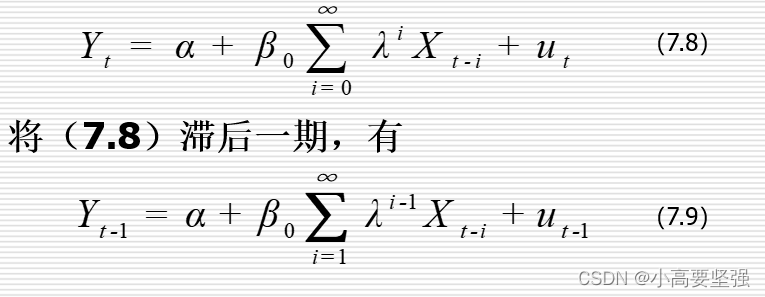
然后两式相减得：

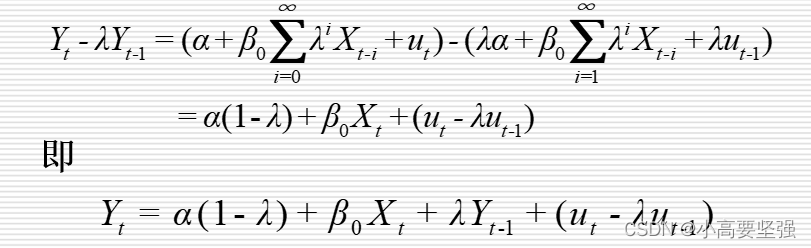
最后，令

这是一个一阶自回归模型。所以我们估计新模型的参数后，即可计算出原模型的参数。

1. 库伊克变换的优点：
   （1）该模型以一个滞后被解释变量代替了大量的解释变量，使模型结构得到极大简化，最大限度地保证了自由度，解决了滞后长度难以确定的相关问题。
   （2）同时，滞后一期的被解释变量与Xt的线性相关程度将低于X的各滞后值之间的相关程度，从而在很大程度上缓解了多重共线性问题。

2. 库伊克变换的缺陷:
   （1）它假定无限滞后分布呈几何滞后结构，即滞后影响按某固定比例递减，解释变量当期值对被解释变量影响最大，滞后一期次之，以此类推。
   （2）新模型的随机扰动项存在一阶自相关，且与解释变量Yt-1相关。
   （3）将随机变量Yt-1作为解释变量引入模型，不一定符合基本假定。
   （4）库伊克变换是纯粹的数学运算结果，缺乏一定经济理论依据。

二、自适应预期模型

某些经济变量的变化会或多或少地受到另一些经济变量预期值的影响，即解释变量预期值会影响被解释变量，所以我们可以将解释变量预期值引入模型建立“期望模型”。例如，预期股票价格会影响现在股票的需求。

包含一个预期解释变量的“期望模型”可以表现为如下形式：

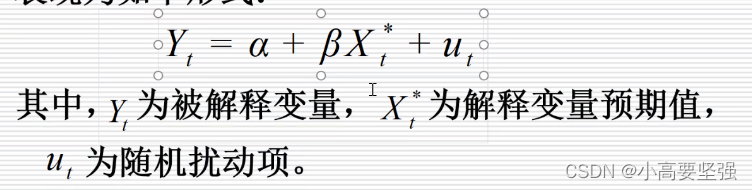
自适应预期假定：经济活动主体对某经济变量的预期是通过一种简单的学习过程而形成的，其机理是，经济活动主体会根据自己过去在作预期时所犯错误的程度，来修正他们以后每一时期的预期，即按照过去预测偏差的某一比例对当前期望进行修正，使其适应新的经济环境。用数学式子表示就是

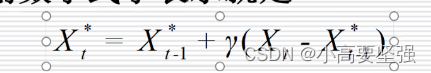
参数r为调节系数，也成为适应系数。这一调整过程称为自适应过程。

将上式也可转化为：

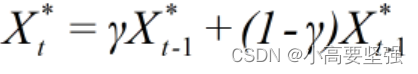
通常，将解释变量预期值满足自适应调整过程的期望模型，称为自适应预期模型。
将Xt预期值代入期望模型，再与代入后的期望模型滞后一期乘以1-r相减，整理得：

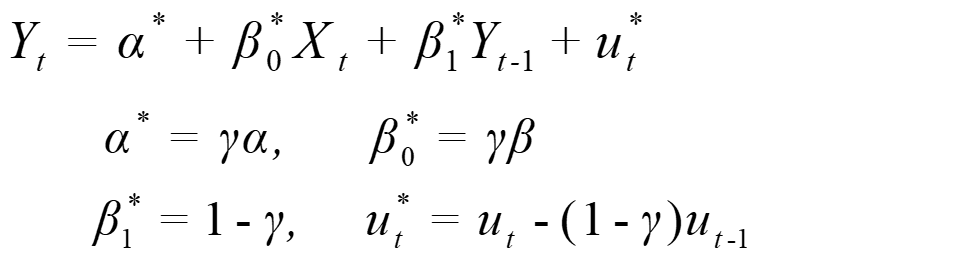
这是一个一阶自回归模型，如果得到该模型参数估计值，代入转换式，就可以求得自适应预期模型的参数估计值。

三、局部调整模型

在经济活动中，会遇到为了适应解释变量的变化，被解释变量有一个预期的最佳值与之对应的现象。例如，企业为确保生产或供应，必须保持一定的原材料储备，对应于一定的产量或销售量，存在着预期最佳库存量；也就是说，解释变量的现值影响着被解释变量的预期值，即存在如下关系：

由于技术、制度、市场及管理等各方面的限制，被解释变量的预期水平在的单一周期内一般不会实现，而只能得到部分调整。局部调整假设认为，被解释变量的实际变化仅仅是预期变化的一部分，即：

故满足局部调整假设的式子（7.22），称为局部调整模型。局部调整假设式（7.23）也可写成：

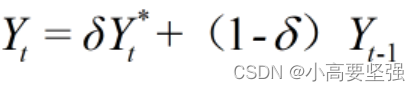
把式（7.22）代入上式，可写出局部调整模型的转化形式：

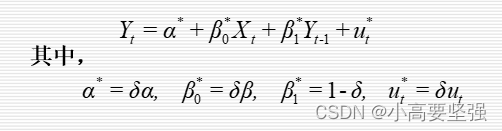
最后进行参数估计。

1、三个模型的相同点和不同点

1. 相同点
   库伊克模型、自适应预期模型与局部调整模型的最终形式都是一阶自回归模型，这样，对这三类模型的估计就转化为对相应一阶自回归模型的估计。

2. 不同点
   导出模型的经济背景与思想不同，库伊克模型是在无限分布滞后模型的基础上根据库伊克几何分布滞后假定而导出的；自适应预期模型是由解释变量的自适应过程而得到的；局部调整模型则是对被解释变量的局部调整而得到的。
   由于模型的形成机理不同而导致随机扰动项的结构有所不同，这一区别对模型的估计带来一定的影响。

2、扩展

当然我们有时可根据需要将局部调整模型与自适应期望模型结合起来对某一经济问题进行研究，及监理局部调整–自适应期望综合模型。

第四节 自回归模型的估计

一、自回归模型估计的困难

一阶自回归模型中的解释变量中含有滞后被解释变量Yt-1，Yt-1是随机变量，它可能与随机扰动项相关，而且随机扰动项可能自相关，也就是说，模型可能违背古典假定，从而给模型的估计带来一定困难。我们来考察上述三个模型对应的一阶自回归模型中随机扰动项的特征。

（1）对于库伊克模型，有

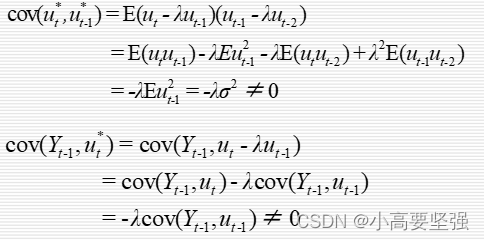
（2）同理可证，对于自适应预期模型有

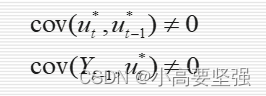
（3）对于局部调整模型有：

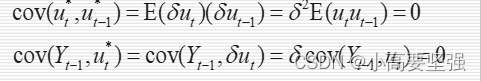
由此可见，对自回归模型进行估计时主要存在两个主要问题，一是出现了随即解释变量Yt-1可能与随机扰动项相关；二是随机扰动项可能自相关。库伊克模型与自适应预期模型的随机扰动项都会导致自相关，只有局部调整模型的随机扰动项无自相关。因此不能直接用最小二乘法直接估计自回归模型。因此。估计自回归需要解决两个问题：一是消除Yt-1与随机扰动项的相关性，二是检验随机扰动项是否存在自相关。
为了缓解随机扰动项与解释变量Yt-1存在相关带来的估计偏倚，可采用工具变量法；诊断一阶自回归模型扰动项存在是否自相关，可用德宾h检验法。而对于扰动项自相关的处理，问题较复杂，涉及动态回归模型的深入内容，在此从略。

二、工具变量法

所谓工具变量法，就是在进行参数估计的过程中选择适当的工具变量，代替回归模型中同随机扰动项存在相关性的解释变量。工具变量的选择应满组以下条件：1、与所代替的解释变量高度相关；2、与随机扰动项不相关；3、与其他解释变量不相关，以免出现多重共线性。
可以证明，利用工具变量法所得到的参数估计是一致估计。

在实际应用，工具变量有多种选择方式。例如，可以选择Yt-1的估计作为工具变量，去代替滞后被解释变量Yt-1进行估计。

这里Yt-1的估计是Yt估计的滞后值，Yt估计是Y对X的滞后值的回归，即由如下回归方程得到：

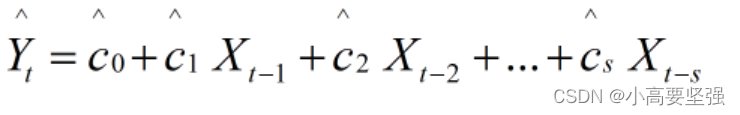
滞后项s适当选取，一般取2或3。

三、德宾h检验

关于随机扰动项是否存在自相关的诊断，可使用前面曾介绍过DW检验法，但这一检验方法不适合于方程含有滞后被解释变量的场合（见DW检验的假设条件）。在自回归模型中，滞后被解释变量是随机变量，已有研究表明。如果用DW检验法，则d统计量值总是趋于2，即倾向于得出非自相关的结论。

对于自回归模型中自相关的检验，除了可以使用能检验模型解释变量中有滞后被解释变量情况的B-G检验方法外，德宾还提出了检验一阶自相关的h统计量检验法。

h统计量定义为：

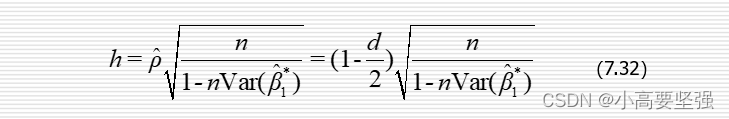
式中，p的估计为随机扰动项一阶自相关系数p的估计量；d为d统计量；n为有效样本容量，Var(B1*估计)为滞后被解释变量Yt-1的回归系数的估计方差。

德宾证明了在p=0的假定下，h统计量的极限分布为标准正态分布。因此，在大量样本情况下，可以用h统计量判断随机扰动项是否存在一阶自相关。
具体做法如下：
（1）对一阶自回归方程直接进行最小二乘估计，得到Var(B1的估计)及d统计量值。
（2）将Var(B1的估计)及d统计量值代入h统计量中，计算h统计量值。
（3）给定显著性水平a，查标准正态分布表得临界值ha。若h的绝对值大于ha/2，则拒绝原假设p=0，说明自回归模型存在一阶自相关。

说明:该检验犯法适用于任何阶的自回归模型。此外，该检验法是针对大样本的，用于小样本效果较差。当nVar(B1*的估计)>1时，不能直接使用该方法。

本文章主要参考庞皓老师计量经济学第四版总结而成。