本文主要是介绍数论数学:斐波那契与黄金分割数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
斐波那契与黄金分割数
详见生成函数(一),里面有对斐波那契数列通项公式的推导。可以得出斐波那契通项公式为:
f ( n ) = 1 5 . [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] f(n)=\frac1{\sqrt5}.[(\frac{1+\sqrt5}{2})^n-(\frac{1-\sqrt5}{2})^n] f(n)=51.[(21+5)n−(21−5)n]
由于 ∣ 1 − 5 2 ∣ < 1 |\frac{1-\sqrt5}{2}|<1 ∣21−5∣<1所以当n足够大的时候 f ( n ) f(n) f(n)与 f ( n − 1 ) f(n-1) f(n−1)的比非常接近黄金分割比 φ = 1 + 5 2 \varphi=\frac{1+\sqrt5}{2} φ=21+5。
黄金分割数与斐波那契
设 η = φ − 1 = 1 − 5 2 \eta=\varphi^{-1}=\frac{1-\sqrt5}{2} η=φ−1=21−5
尝试把 η n \eta^{n} ηn表示成 a n η + b n a_n\eta+b_n anη+bn的形式(显然可以)
发现, b n b_n bn就是斐波那契数列。
斐波那契与杨辉三角(帕斯卡三角)
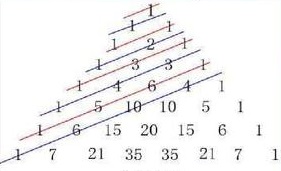
在每条直线上求和即为斐波那契数列
斐波那契与自然
这个是小学数学课上,老师讲到斐波那契之类的话题时必讲的内容(估计他们认为讲别的小学生也听不懂)。但是我们说的“ 斐波那契与自然”在定义上有一些不同。
首先是汤姆孙问题。这个问题是在1907年物理学家J.J.汤姆孙发现了电子,提出了“电子浸浮于均匀正电球”的原子结构模型(汤姆孙模型)。在均匀正电球上,由于电子互相排斥,所以电子在球上的排列方式应该是一种使电子间距离的最大值最小的方案。汤姆孙问题就是求这种方案的。
如果把正电球看做液滴,而电子是球上的一些特殊点,那么这个液滴滴在平面上的时候,电子的排列图案刚好与向日葵花盘的图案一样。
这篇关于数论数学:斐波那契与黄金分割数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







