Reinforcement Mechanism Design：With Applications to Dynamic Pricing in Sponsored Search Auction

【论文阅读】Reinforcement Mechanism Design : With Applications to Dynamic Pricing in Sponsored Search Auctions

1 本文解决了什么问题？

本文旨在结合机制设计和强化学习来解决 搜索引擎的动态定价问题（dynamic pricing problem）。在该场景中，通过与投标人的反复互动，搜索引擎可以动态地改变保留价格，并确定最优策略，使得利益最大化。

赞助搜索拍卖：当用户在搜索引擎提交了一个查询后，搜索引擎会在结果页面中显示一些与结果相关的广告。于是，关键字搜索在所有对关键字感兴趣的广告商中触发拍卖机制。广告商提交投标，来争夺搜索结果页面上的广告位置。随后，搜索引擎根据广告商的出价，对结果页面的广告进行排名，只有在有人点击广告时才向他们收费。

在赞助搜索拍卖中的黄金标准机制是 广义第二价格（GSP）拍卖。拍卖将最好的广告位分配给出价最高的广告商，第二好的广告位分配给出价第二高的广告商，以此类推；并按照他们低一个的位置的出价价格收费（或者以最低的价格让他们维持当前的位置）。

但 GSP 的问题是，它并非收益最优的。在标准博弈论的假设下，收益最优的拍卖不一定会根据他们的出价排名来分配位置。并且，在最优拍卖中，通常存在一个保留价格（reserve prices）来过滤广告商的低出价。近年来，有大量的文献通过对排名和保留价格的设计来对 GSP 收益优化。

然而，大多数收益优化理论都主要依赖于对投标人理性行为的假设。最近的研究表明，这种假设在现实中可能并不成立。

本文提出使用 强化机制设计（reinforcement mechanism design） 来解决该问题，大致思路如下：

1. 首先，作者遵循机制设计理论，使用一组参数来表述本文的机制；
2. 然后，作者使用优化算法来搜索机制的最优参数。

为了解决“二阶”效应，即 投标人在不同机制下有不同的行为，作者使用机器学习算法建立了明确以机制参数为输入的投标人动作模型。投标人动作模型包括了公共特征集和私有特征集，利用投标人可观测的特征直接预测投标人动作。

本文放宽了不现实的假设，并考虑在一个环境中，投标人可以拥有任意复杂的私有信息和任意的理性水平，可以随着时间动态变化。正是因为 投标者行为模型不依赖他们的私有信息，而是定义在投标人的观测和历史投标数据上，才能达到此目的。

2 本文提出的解决方法是什么？

2.1 先验知识

赞助搜索拍卖（Sponsored search auction）

当用户在搜索引擎中输入关键字查询时，搜索引擎（即卖方）会在结果页面中显示一些与关键字相关的广告。本文考虑对单个关键字的拍卖，有 $N$ 个竞标者，竞争 $K$ 个广告位置。每一个竞标者 $i$ 会给卖方报告一个出价 $b_i$，因此一个 竞标概要（bid profile）表示为 $b=\left(b_1,b_2,\dots ,b_N\right)$。本文稍微滥用符号 $b_i$，同时用来指代竞标者 $i$ 以及他的出价。

本文的目标是 设计一个动态机制，使得在实践中能够产生长期的竞争性收益。

广义二价拍卖（GSP auction）机制

在收到搜索查询后，卖方需要确定一个位置分配方案和支付向量。一个机制形式化的表示为两个函数的组合 $\mathcal{M}=(x,p)$，其中，分配规则 $x$ 是一个函数 $x:{\mathbb{R}}^N\to [0,1{]}^N$，以竞标概要作为输入，输出一个 $N$ 维向量，该向量表示分配给每个竞标者的项目数量；支付规则 $\rho$ 为函数 $p:{\mathbb{R}}^N\to {\mathbb{R}}^N$，它将竞标概要映射到 $N$ 维非负向量，指定每个竞标者的支付。

在 GSP 拍卖中，假设有 $N$ 个竞标者和 $K$ 个广告位。这 $K$ 个广告位在吸引用户点击方面具有不同的效果（由其点击率 CTRs 来表示）。第 $k$ 个广告位的点击率表示为 $q_k$，并假设 $q_k$ 相对于广告位的增长是非增的，即 $q_1\ge q_2\ge \cdots \ge q_K\ge 0$。

在收到搜索关键字后，卖方首先从投标人处搜集竞标概要 $b$。通常，每个竞拍者都有一个保留价格（reserve price）$r_i$，这是投标人 $i$ 需要投标的最低数量以进入拍卖。本文使用 $b_{(i)}$ 表示高于保留价的出价中，第 $i$ 高的出价。然后，卖方按顺序将第 $i$ 个广告位分配给投标人 $b_{(i)}$，直到广告位或者出价者耗尽为止。当竞标者 $b_{(i)}$ 的广告被用户点击时，卖方会根据下面的规则向竞标者收费。
$$p_{(i)}=\{\begin{array}{ll}\max \left\{\frac{q_{i+1}{b}_{(i+1)}}{q_i},r_{(i)}\right\}& \text{ if }{b}_{(i+1)}\text{ exists; }\\ r_{(i)}& \text{ otherwise. }\end{array}$$
保留价格 $r$ 会显著影响广告平台的收益。在本文中，作者将保留价格作为该机制的主要参数，卖家的目标是动态设置保留价格，以最大化其收入。

2.2 投标者行为模型

机制设计理论很大程度上依赖于投标人的行为。经典的博弈论分析依赖于以下假设：

• 投标者具有准线性效用；
• 投标者拥有无限的信息获取和计算能力来计算纳什均衡；

然而，这些假设在现实中会存在问题。首先，不同的投标者可能有不同的广告宣传的目的。例如，想要提高品牌知名度的竞标者可能只关心印象数量，而预算有限的竞标者想要提高销量，则可能会关注广告在特定时段的点击量。第二，在真实的广告平台中，竞标者只能访问自己的广告信息（私有信息）。经验证据还表明，上述假设可能不适用于赞助搜索拍卖

基于 RNN 的投标者模型

在本文的模型中，每个投标者的行为就是他的投标分布。投标形成分布的原因是投标人可以针对不同的用户特征进行不同的投标。每个投标人 $i$ 是一个函数 $g_i$，它以历史投标分布及其 KPIs（关键绩效指标）作为输入，输出投标者下一个时间步的投标分布。为了拟合这些时间序列数据，作者使用标准的长短时记忆（LSTM）循环神经网络。RNN 的输出进一步通过一个通用的全连接 softmax 激活函数进行转换，以确保网络的最终输出是一个有效的概率分布。网络的输入包括连续 $m$ 天的 KPIs、投标者的投标分布以及一些与日期相关的特征。

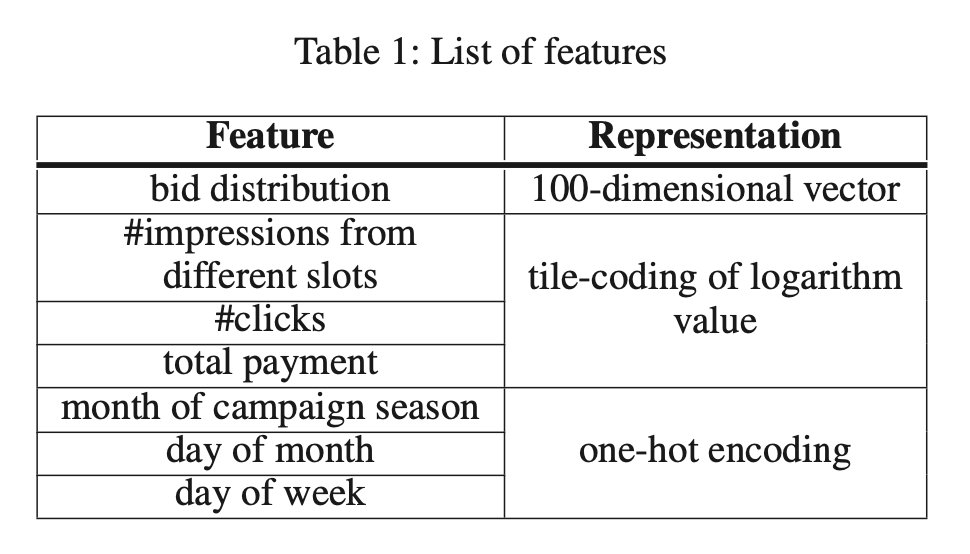
为了简化投标分布的表示，作者将 100 个非重叠区间离散化，并使用 100 维向量 $b$ 来描述投标分布。这 100 个时间间隔是根据历史数据计算的，因此每个时间间隔包含所有投标人的投标数量大致相同。

作者为每个投标者选择的 KPI 统计数据包括投标者从每个广告位置获得的 印象次数、**获得的总点击次数 **和 支付的总金额。作者在百度中观察到，竞标者更关心 KPIs 的相对变化，而不是绝对变化。例如，100 次点击量的增加对每天获得 200 万次点击的竞标者没有任何影响，但对每天获得 200 次点击的小竞标者来说就相当重要了。因此，为了捕捉这种相对变化，作者将这些 KPI 统计数据的对数值 作为 RNN 的输入特征，并使用 tile-coding 进行编码。

除了上述私有特性，模型中还包括一个公共特性集，包括日期相关的特性，如月份和星期几。所有这些特性都是用 one-hot encoding 编码的。包含这些功能的原因是，大多数广告商有季节性的广告活动，并可能根据当前日期调整他们的报价策略。

公式：马尔可夫投标者模型

本文采用时间同质的马尔可夫模型来解释基于 RNN 的投标者行为模型。投标者 $i$ 在时间步 $t$ 的投标分布表示为 $s_i^{(t)}$，接收到的 KPIs 表示为 $h_i^{(t)}$。投标者可以根据他们的 KPIs 动态调整他们的投标。因此，投标人 $i$ 在下一个时间步的投标分布是之前的 $s_i$ 和 $h_i$ 的函数:
$$s_i^{(t+1)}=g_i\left(s_i^{(t-m+1:t)},h_i^{(t-m+1:t)}\right)$$
其中，$s_i^{(t-m+1:t)}$ 和 $h_i^{(t-m+1:t)}$ 分别表示投标者 $i$ 在 $m$ 个连续时间上的投标分布和 KPIs。

2.3 强化机制设计框架

如何将动态机制设计表述为马尔可夫决策过程？

假设每个投标都是相互独立的，虽然这种假设失去了普遍性，但事实上它在许多工作中被广泛使用。联合投标分布 为：
$$\begin{array}{rl}{s}^{(t+1)}& =\prod _{i=1}^N{s}_i^{(t+1)}=\prod _{i=1}^N{g}_i\left(s_i^{(t-m+1:t)},h_i^{(t-m+1:t)}\right)\\ & =g\left(s^{(t-m+1:t)},h^{(t-m+1:t)}\right)\end{array}$$
为了简单起见，作者假设每个关键字的日查询次数是一个常量。因此，KPIs $h^{(t)}$ 完全由投标分布 $s^{(t)}$ 和保留价格 $r^{(t)}$ 所决定。因此，本文将动态机构设计问题表述为一个马尔可夫决策过程，将 $s^{(t)}$ 视为卖方的状态，$r^{(t)}$ 视为卖方的动作。

Definition 1. 长期收益最大化问题是一个马尔可夫决策过程 $(\mathcal{N},S,R,G,REV(s,r),\gamma )$，其中

• $\mathcal{N}$ 是投标者（竞标者）的集合，$|\mathcal{N}|=N$；
• $S=S_1\times \cdots \times S_N$ 为状态空间，其中 $S_i$ 为投标者 $i$ 所有可能的投标分布的集合；
• $R=R_1\times \cdots \times R_N$ 为动作空间，其中 $R_i$ 为机制设计者为投标者 $i$ 设计的所有可能的保留价格的集合；
• $G=\left(g_1,g_2,\dots ,g_N\right)$ 为状态转移函数；
• $REV(s,r)$ 为瞬时奖励函数，在状态 $s$ 设置保留价格 $r$ 所获的的期望收益。
• $\gamma$ 为折扣因子，$0<\gamma <1$。

该任务的目标是选择一个使折扣收益之和最大化的保留价格序列 $\left\{r^{(t)}\right\}$：
$$OBJ=\sum _{t=1}^{\infty }{\gamma }^{t}REV\left(s^{(t)},r^{(t)}\right)$$
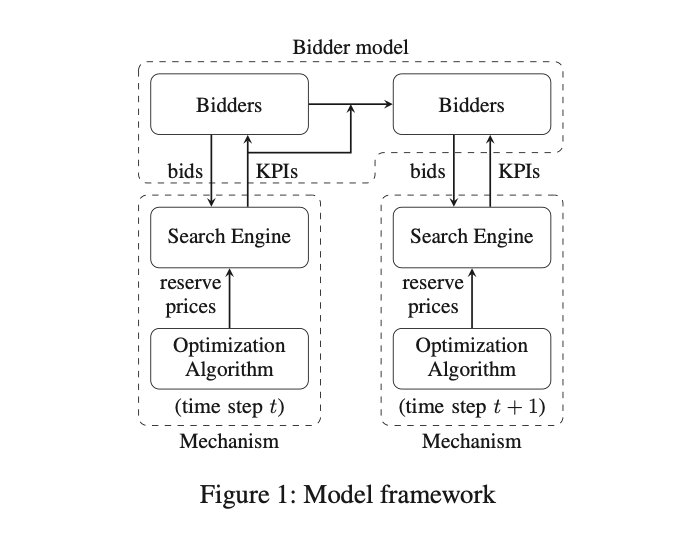
下图展示了本文动态机制设计的主要框架，其中包含了两个部分：

1. 马尔可夫投标者行为模型（基于 RNN），它决定了投标者如何根据 KPIs 反馈来调整他们的投标；
2. 机制，投标人与卖方的行动（保留价格）互动，并获得 KPIs 作为反馈。

优化算法：MCTS

根据MDP理论，虽然存在一个最优的保留定价方案，但其精确计算的成本非常高，原因如下:

• 可能的保留价格概要与投标人的数量成指数增长；
• 要探索的未来状态数与搜索深度成指数关系。

作者通过将注意力限制在 只包含几个主要投标人的关键字上，来规避第一个困难。作者关注稀疏市场（少数主要投标人）的关键字，主要是因为保留价格的影响力会在稠密市场中减弱。

为了解决第二个问题，作者 只探索在当前保留价格附近的投标人可能采取的行动。这一限制对于实际的稳定性问题也是必要的，因为保留价格的突然变化将导致投标人的 KPIs 的突然变化，这将损害平台的稳定性。

有了这些限制，动作空间的大小就减少到一个小子集。为了进一步加快搜索速度，我们实现了蒙特卡洛树搜索（MCTS）算法，因为 MCTS 算法可以通过限制搜索深度和搜索轨迹的数量来有效地限制其计算复杂度。

3 有什么关键的实验结果？

作者选择了 400 个具有以下属性的关键字：

1. 该关键字的每日查询数量很大且稳定（方差很小）；
2. 大部分（至少 80 %）的收入，关键字贡献最多3个投标人。

作者从百度中提取了与这些关键词相关的 8 个月的竞价数据。数据集的总数据大小超过 70 TB。数据集中的这 400 个关键词贡献了百度总收益的 10%。每个数据记录对应于广告的印象，包含 300 多个数据字段。

3.1 投标者行为模型

对每个关键字，作者只关注 3 大投标人，而忽略其他投标人。对于每个投标人，作者使用 TensorFlow 构建了一个具有 128 个隐藏单元的 LSTM 递归神经网络。将时间步长设为 1 天，利用 8 个月的数据进行训练。使用平均交叉熵作为性能指标，并使用 Tensorflow 内置的 ADAM 优化器优化 RNN。将总数据集分为 90% 的训练集和 10% 的测试集。

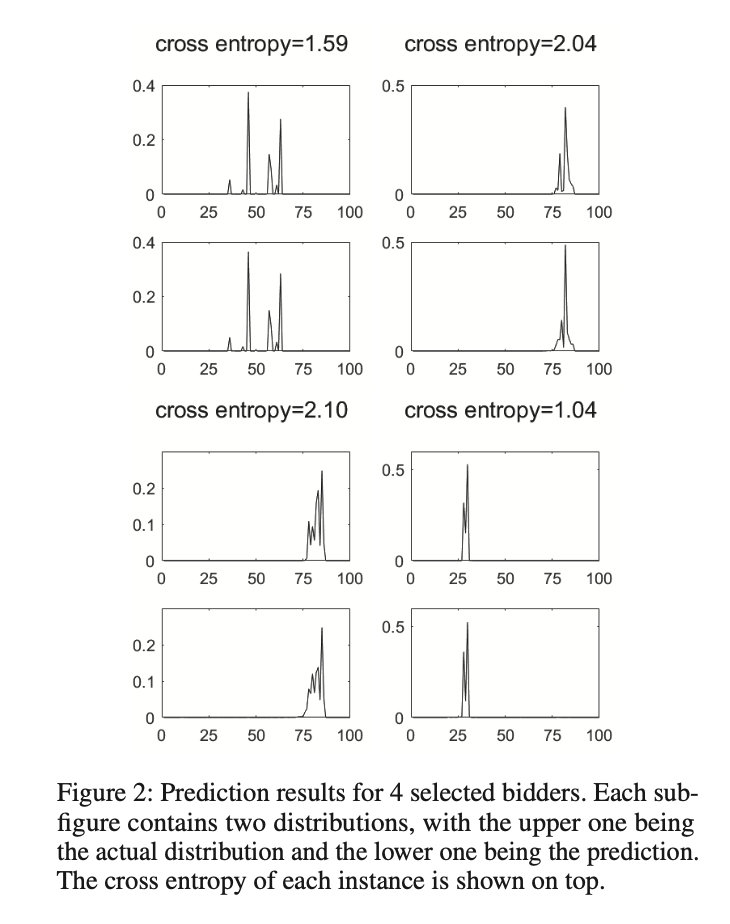
RNN 的输入是连续 $m$ 天的投标分布和 KPIs。我们在实验中设置 $m=4$，在测试集中所有投标人和所有测试实例中平均交叉熵约为1.67。

3.2 MCTS

作者为投标人探索的可能的保留价格是目前保留价格的 0.95，1.0 和 1.05 倍。在优化算法中，作者设置 $\lambda =0.8$，搜索深度为 5。在选择步骤中，作者将探索次数限制为 5000 次。在扩展步骤中，为了估计所选节点的收益，作者模拟拍卖 500万 次，并计算出平均收益作为每个关键字的每印象收益。

作者将初始保留价设为 $p=\arg {\max }_{b}b(1-F(b))$，其中 $F(b)$ 为当前的投标分布。本文称这个保留价格为 静态最优，因为如果投标人不改变他们的出价，这个价格会使收益最大化。对比方法：

1. STATIC_OPT：一直使用初始保留价格；

2. GREEDY：设当前时期的收入为 $RE{V}^t$。在每一轮中，随机选择一个投标者 $i$，只改变他的保留价 −5%，并模拟下一阶段的拍卖。收入为：
   $$RE{V}_i^{t+1}=REV\left(s^{(t+1)},\left(0.95r_i^{(t)},r_{-i}^{(t)}\right)\right)$$
   于是，设置：
   $$r^{(t+1)}=\{\begin{array}{ll}\left(0.95r_i^{(t)},r_{-i}^{(t)}\right)& \text{ if }RE{V}_i^{t+1}>RE{V}_i^t\\ (1.05r_i^{(t)},r_{-i}^{(t)}& \text{ otherwise }\end{array}$$
   注意，这个方法可以看作是坐标梯度下降（上升）方法的简化版本。

3. POLICY_GRAD：该算法类似于对每个投标人同时应用 GREEDY 算法。在该算法中，我们计算每个投标人 $i$ 的收入变化，并相应地改变保留价格：
   $$r_i^{(t+1)}=\{\begin{array}{ll}0.95r_i^{(t)}& \text{ if }RE{V}_i^{t+1}>RE{V}_i^t\\ 1.05r_i^{(t)}& \text{ otherwise }\end{array}$$

4. BAIDU：百度当前使用的保留价格

5. STATIC_50：为所有投标人的保留价格都设置为 50分，无论投标分配。

3.3 结果与分析

在第一个实验中，作者在 MCTS 算法中设置 $\Delta t=1$，并与上述其他策略进行比较，为每种策略模拟 120 天。实验结果如下图所示，收益根据百度的收敛值进行归一化。

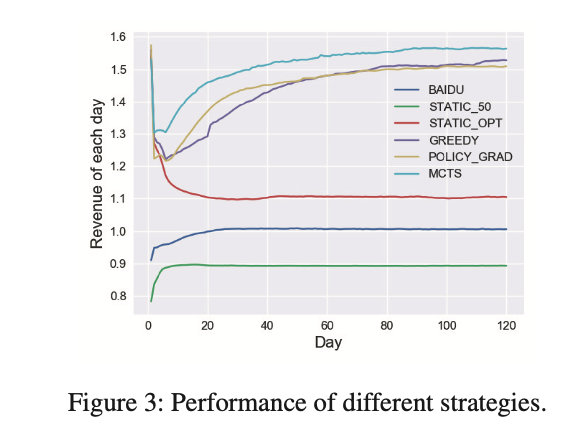
结果分析：

• 本文提出的动态策略最优；
• BAIDU 曲线在短短几天内迅速收敛。它在一开始会略微上升，主要是因为作者在模拟使用了确定性的保留价格，而不是实际的随机保留价格。
• STATIC_OPT 曲线在第一天快速上升，然后急剧下降，两周后收敛。

事实上，在之前的百度在线实验中，作者为每个（关键字，投标人）对设置了 STATIC_OPT 保留价格，以测试投标人的反应。实验表明，根据历史出价设定一个能最大化即时收益的保留价，可能会在短期内带来高收益，但在 10 到 20 天左右后会回落。此外，该策略使收敛后的收益增加约 10%。

此外，模拟还揭示了投标人行为的一些有趣事实：

• 所有激进的定价方案都能在短期内获得高收益，随后大幅下降。这种现象对于我们的数据集来说是固有的，因为由于相对较低的保留价格和随机折扣，所有的竞标者之前都经历了温和的定价机制。保留价的突然变化（采用静态最优保留价和放弃随机）可以立即获得巨大的回报，但一旦投标人意识到这种变化并做出相应的反应，可以提取的收益就会减少。
• 虽然 STATIC_OPT 可以击败温和的机制，如 BAIDU 和STATIC_50，但它的长期收益并不像短期收益那样优秀。
• 实验表明，引入更多的优化算法（如MCTS）和精确的投标模型，可以获得最佳的性能，并获得更高的长期收益。
• 令人惊讶的是，算法 GREEDY 和 POLICY_GRAD 的表现非常好，只比 MCTS 算法略差。然而，这两种算法要简单得多，而且计算成本更低。这样的结果在某种程度上可能表明竞标者不是很有策略，因为像 GREEDY 这样的简单算法也可以很好地捕捉他们的行为。
• GREEDY 算法和 POLICY_GRAD 算法是相似的，并且具有相似的性能。POLICY_GRAD算法曲线更平滑，收敛速度更快，而 GREEDY 算法收敛时收益略高。

在第二个实验中，作者 比较了保留价格变化频率的影响。结果如下图所示。作者使用 MCTS 算法，每个 $\Delta t$ 也模拟了 120天 。从图中可以看出 $\Delta t$ 越小，它可以提取的收入越多，收敛的速度也越快。$\Delta t=7$ 的收益比 $\Delta t=1$ 的收益少了几个百分点，对比图 3 和图 4，可以看到，GREEDY 算法的性能几乎与 $\Delta t=3$ 的 MCTS 算法相同。

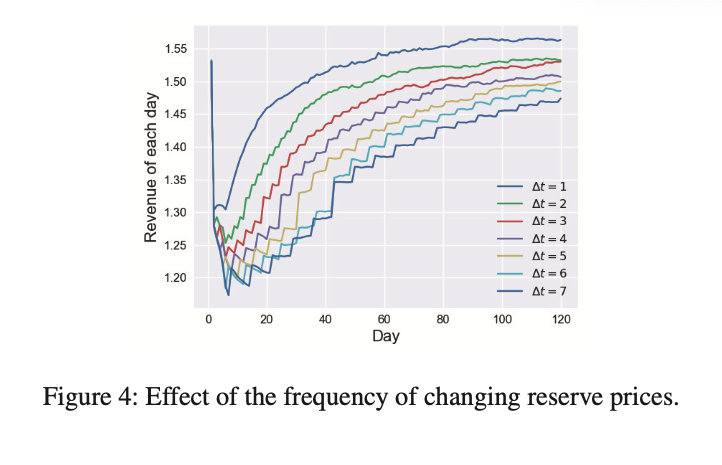
显然，频繁改变保留价格会影响平台的稳定性，因此是不可取的。在这个实验中，作者只比较框架的性能。