本文主要是介绍2022全国大学生数学建模大赛C题——古代玻璃制品的成分分析与鉴别,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基于随机森林分类的古代玻璃制品的成分分析与鉴别
摘要
本文主要针对古代玻璃制品成分分析与鉴别的问题,对因为受掩埋环境的影响,从而改变其原本的化学成分古代玻璃制品,建立随机森林分类模型对其风化前化学成分进行预测和分类。同时采用bp神经网络分类模型、相关性分析等分别对建立模型进行分析和求解,以此来对其类别进行正确的判断。
首先,我们对给出的数据进行预处理,剔除化学成分总含量不在85%-105%范围内的数据,对数据中的空缺值作置零处理。
对于问题一,首先我们采用卡方检验来对玻璃文物表面分化与其玻璃类型、纹饰和颜色的关系进行分析。部分结果如下表:
| 特征 | 名称 | 表面风化 | 总计 | |
| 风化 | 无风化 | |||
| 颜色 | nan | 4 | 0 | 4 |
| 浅绿 | 1 | 2 | 3 | |
| 浅蓝 | 16 | 8 | 24 | |
其次,我们将高钾类型和铅钡类型分为风化和无风化,并可视化其各化学成分含量,对比分析其统计规律。利用独立样本t检验分析有无风化成分含量是否存在差异性,最后利用独立样本t检验结果计算有无风化的均值比例,利用该比例求得其不同类型玻璃文物风化前的化学成分含量。
对于问题二,我们建立随机森林分类模型,分析各个化学成分所占的特征比重,对两个类型的玻璃文物进行划分。在此基础上对不同类别分别进行聚类分析,划分出其亚分类,并对结果进行合理性和敏感性的分析。
对于问题三,我们在问题二的基础上,利用随机森林分类模型对未知类别玻璃文物的化学成分进行分析,并鉴别其所属类型。为保证预测结果的准确性,同时建立bp神经网络分类模型、决策树分类模型对其化学成分分析,鉴别类型。对比分析三个模型的预测结果,得到较为准确的求解方法,并对其结果进行灵敏性检验。部分结果如下表:
| 预测结果_Y | 预测结果概率_铅钡 | 预测结果概率_高钾 | 氧化锶(SrO) | 氧化钙(CaO) | 二氧化硫(SO2) | 氧化锡(SnO2) | 氧化铅(PbO) | 氧化铁(Fe2O3) | 五氧化二磷(P2O5) | 氧化铜(CuO) | 氧化钡(BaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 二氧化硅(SiO2) |
| 高钾 | 0.13 | 0.87 | 0.03 | 6.08 | 0.51 | 0 | 0 | 2.15 | 1.06 | 2.11 | 0 | 1.86 | 7.23 | 78.45 |
| 铅钡 | 0.88 | 0.12 | 0 | 7.63 | 0 | 0 | 34.3 | 0 | 14.27 | 0 | 0 | 0 | 2.33 | 37.75 |
对于问题四,我们将两个不同类型的玻璃文物分别对其化学成分进行相关性分析在此基础上比较不同类型玻璃文物的化学成分关联关系的差异性。
关键字 随机森林 聚类分析 bp神经网络 相关性分析 决策树分类
- 问题的提出
丝绸之路是古代中西方文化交流的通道,其中玻璃是早期贸易往来的宝贵物证。早期的玻璃在西亚和埃及地区常被制作成珠形饰品传入我国,我国古代玻璃吸收其技术后在本土就地取材制作,因此与外来玻璃制品的外观相似,但是化学成分不同。
古代玻璃极易受埋藏环境影响而风化。在风化过程中,内部元素与环境元素进行大量交换,导致其化学成分发生改变。因此提出以下问题:
1.据附件表单1给出的文物分类信息,对这些玻璃文物的表面分化与其玻璃类型、纹饰和颜色进行分析。结合高钾玻璃和铅钡玻璃这两种玻璃的类型,分析文物样品表面有无化学成分含量的统计规律,并根据附件2给出的分化点检测数据,预测其风化前的化学成分含量。
2.根据附件数据分析高钾玻璃和铅钡玻璃的分类规律,并且给出具体的方法来选择合适的化学成分作为分类依据分别对高钾和铅钡玻璃进行亚类划分,得出相应结果,最后还仍要析分类结果的合理性和敏感性。
3.据附件表单3中未知类别玻璃文物的化学成分进行分析,鉴别其所属类型,并对分类结果的敏感性进行分析。
4.问题四要求分析不同类别的玻璃文物样品的化学成分之间有何关联关系,并且给出其关联关系的差异性。
二、问题的分析
问题一:据题目要求,我们首先将对数据进行预处理,通过Excel函数的筛选功能进行筛选,将成分比例累加和介于85%~105%之间的数据保留,并将缺失值做置零处理。对于第一小问,我们采用卡方检验来对这些玻璃文物的表面分化与其玻璃类型、纹饰和颜色的关系进行分析。对于第二小问,我们将表二的数据分为四组,分为高钾分化、高钾无分化、铅钡分化、铅钡无分化,将其成分含量进行可视化处理,并分别对组内样本化学成分含量进行独立性T检验,从而得出统计规律。对于第三小问,我们依据独立样本t检验的结果计算出分化和无分化的均值比例,并利用该比例求得分化前的化学成分含量。
问题二:建立随机森林分类模型,分析各个化学成分所占的特征比重,对两个类型的玻璃文物进行划分。在此基础上对不同类别分别进行聚类分析,划分出其亚分类,对特征比重较大的化学成分放大5%和缩小5%作为扰动数据,对结果进行合理性和敏感性的分析。
问题三:在问题二的基础上,利用随机森林分类模型对未知类别玻璃文物的化学成分进行分析,并鉴别其所属类型。为保证预测结果的准确性,同时建立bp神经网络分类模型和决策树模型对其化学成分分析,鉴别类型。对比分析三个模型的预测结果,得到较为准确的求解方法,并对其结果进行灵敏性检验。
问题四:我们将两个不同类型的玻璃文物分别对其化学成分进行相关性分析在此基础上比较不同类型玻璃文物的化学成分关联关系的差异性。
- 模型假设
针对本文提出的有关玻璃制品成分鉴别与分析的问题,我们做了如下的模型假设:
1.假设未检测到的化学成分在玻璃文物中不存在,即含量为0。
2.假设在考虑风化前后玻璃类型以及化学成分含量变化时不考虑时间的影响。
3.假设在进行分类讨论时不考虑颜色和纹饰对结果造成的影响。
4.假设在选择合适的指标时,仅考虑显著性p值造成的影响,不考虑其他因素的影响。
四、符号说明
本文常用符号见下:
| 符号 符号说明 |
| A 实际值 T 理论值 X2 卡方检验 df 自由度 R 行数 C 列数 T 独立样本T检验的统计量 (Xj,Ci) n维空间中的点 d(Xj,Ci) n维空间中两点的欧式距离 xj BP神经网络积累 yi 某个神经元传递过来的刺激量 wji 链接某个神经元刺激的权重 ρ 皮尔逊总体相关系数代表符号 R 皮尔逊相关系数 |
五、模型的建立与求解
经过以上的分析与准备,本文将逐步建立以下数学模型,进一步阐述模型的实际建立过程。
5.1问题一模型的建立与求解
对于问题一,首先需要对玻璃表面风化情况结合类型、纹饰和颜色的差异性进行分析,结合玻璃的类型分析化学成分的变化规律以及预测风化前的化学成分含量,分成以下三个小问题解决:
- 利用卡方检验分析表面分化对其类型、纹饰和颜色的差异性。
- 对不同类型玻璃风化有无风化的数据进行可视化分析,总结化学成分变化规律。
- 利用独立样本t检验,得到玻璃有无风化各化学成分的均值比例,对不同类型未风化时的化学成分进行预测计算。
5.1.1数据的预处理
(1)数据的清洗
我们将对总成分比例不足85%~105%的数据进行删除,并将附件中的空缺值全部进行置零处理,以此来改善后续的数据挖掘分析和建模工作。
(2)数据的填补
附件表单一中的颜色这一栏中有4组缺失值,我们将其进行数据填补,填补为“nan”,意为难以判断其文物的颜色。
(3)数据的集成
本题中要分析文物样品表面有无分化化学成分含量的统计规律,所以我们需对附件表单一和附件表单二中的的数据进行合并,完成数据集成工作。
- 数据的可视化处理
本题为了更直观的呈现出有效信息,更有利与对比分析出统计规律。我们将高钾分化、高钾不分化、铅钡分化、铅钡不分化这四大类的各个化学成分含量进行可视化化处理。
5.1.2针对表面风化情况的模型建立
卡方检验主要应用于推断两个或对个样本率及构成比有无差别的统计推断,从而判断出两个或多个变量的关联性。而本题是分析文物表面分化与玻璃类型、纹饰和颜色的关系,恒适用于此方法。
卡方检验的计算公式为:
 (5-1)
(5-1)
其中A是实际值,T为理论值,则是衡量理论与实际的差异程度。
接着我们根据卡方值来判断是否具有差异性,通过查询卡纸分布的临界值,将计算的值与临界值进行比较。
自由度为:
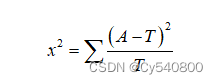 (5-2)
(5-2)
其中R为行数,C为列数。
由自由度查询可得到临界值,如果<临界值,则假设成立。
独立样本T检验是用于分析定类数据(x)与定量数据(y)之间的差异情况。我们在分析有无分化含量的差异性就用到此方法。
在使用独立样本T检验时,数据必须通过正态性检验与方差齐性检验,否则使用非参数检验。
独立样本T检验的统计量为:
(5-3)
 (5-4)
(5-4)
5.1.3针对表面风化情况的模型求解
利用卡法检验的方法针对表面风化情况得到以下卡方检验表:
表5-1 表面分化卡方检验表
| 题目 | 名称 | 表面风化 | 总计 | X² | 校正X² | P | |
| 风化 | 无风化 | ||||||
| 颜色 | nan | 4 | 0 | 4 | 14.466 | 14.466 | 0.070* |
| 浅绿 | 1 | 2 | 3 | ||||
| 浅蓝 | 16 | 8 | 24 | ||||
| 深绿 | 4 | 3 | 7 | ||||
| 深蓝 | 0 | 4 | 4 | ||||
| 紫 | 3 | 2 | 5 | ||||
| 绿 | 0 | 1 | 1 | ||||
| 蓝绿 | 9 | 8 | 17 | ||||
| 黑 | 4 | 0 | 4 | ||||
| 类型 | 铅钡 | 15 | 35 | 50 | 8.429 | 6.911 | 0.004*** |
| 高钾 | 13 | 6 | 19 | ||||
| 纹饰 | A | 15 | 14 | 29 | 5.669 | 5.669 | 0.059* |
| B | 0 | 6 | 6 | ||||
| C | 13 | 21 | 34 | ||||
通过以上卡方检验分析的结果显示,我们可以获得:
对于表面风化,水平上不呈现显著性,因此对于表面风化和颜色数据不存在显著性差异;对于表面风化,水平上呈现显著性,因此对于表面风化和类型数据存在显著性差异;对于表面风化,水平上不呈现显著性,因此对于表面风化和纹饰数据不存在显著性差异。
在此基础上进行效应量化分析,用于分析表面风化与其余三个指标的相关程度,包括以下四个量化指标:
1.phi系数: phi相关系数的大小,表示两样本之间的关联程度。当phi系数小于0.3时,表示相关较弱;当phi系数大于0.6时,表示相关较强。
2. Cramer's V: 与phi系数作用相似,但Cramer's V系数的作用范围较广。当两个变量相互独立时,V=0,当数据中只有2个二分类变量时,Cramer's V系数的结果与phi相同。
3.列联系数:简称C系数,用于3×3或4×4交叉表,但其受行列数的影响,随着R和C 的增大而增大。因此根据不同的行列和计算的列联系数不便于比较,除非两个列联表中行数和列数一致。
4.lambda:用于反应自变量对因变量的预测效果,一般情况下,其值为1时表示自变量预测因变量效果较好,为0时表明自变量预测因变量较差。
结果如下表:
表5-2 表面风化效应量化分析表
| 字段名/分析项 | Phi | Crammer's V | 列联系数 | lambda |
| 颜色 | 0.458 | 0.458 | 0.416 | 0.000 |
| 类型 | 0.350 | 0.350 | 0.330 | 0.000 |
| 纹饰 | 0.287 | 0.287 | 0.276 | 0.057 |
通过表中数据可知:颜色和表面风化的差异程度为中等程度差异;类型和表面风化的差异程度为中等程度差异;纹饰和表面风化的差异程度为中等程度差异。
5.1.4不同类型玻璃表面有无风化的统计分析
首先将不同类型玻璃依据表面有无风化分成四个部分:高钾风化、高钾无风化、铅钡风化、铅钡无风化。依据所给出的数据对以上四个部分进行可视化分析,结果如下图:

分析上图,对比可知高钾玻璃在风化后主要化学成分呈下降趋势,铅钡玻璃在风化后主要化学成分呈上升趋势。
5.1.5不同类型玻璃风化前化学成分的预测
首先,各类型玻璃的化学成分进行独立样本t检验,计算各个化学均值,得到其风化和无风化各个化学成分的均值比例。结果如下图:
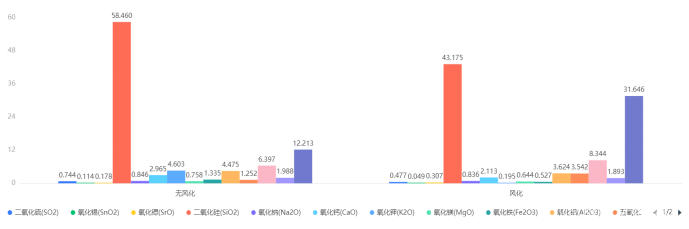
根据图中结果,我们得到无风化和风化各化学成分的均值比例:
二氧化硫(SO2): 0.744/0.477 氧化锡(SnO2): 0.114/0.049
氧化锶(SrO): 0.178/0.307 二氧化硅(SiO2): 58.46/43.175
在氧化钠(Na2O): 0.846/0.836 在氧化钙(CaO): 2.965/2.113
氧化钾(K2O): 4.603/0.195 氧化镁(MgO): 0.758/0.644
氧化铁(Fe2O3): 1.335/0.527 氧化铝(Al2O3): 4.475/3.624
五氧化二磷(P2O5): 1.252/3.542 氧化钡(BaO): 6.397/8.344;
氧化铜(CuO): 1.988/1.893 氧化铅(PbO): 12.213/31.646
依据以上各化学成分的均值比例,我们利用高钾类型和铅钡类型玻璃风化的数据表单对两种类型玻璃未风化前的成分进行简单计算预测,(由于篇幅有限,完整的结果数据将在附件当中给出)以铅钡类型玻璃为例,其未分化前部分各化学成分含量如下表:
表5-3 铅钡玻璃风化前各化学成分含量
| 二氧化硅(SiO2) | 氧化钠(Na2O) | 氧化钾(K2O) | 氧化钙(CaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 氧化铁(Fe2O3) | 氧化铜(CuO) |
| 48.978 | 0 | 24.78 | 3.276 | 1.3806 | 7.0479 | 4.7058 | 0.273 |
| 27.189 | 0 | 0 | 2.072 | 0 | 1.6482 | 0 | 10.9305 |
| 6.2235 | 0 | 0 | 4.466 | 0 | 1.3653 | 0 | 3.297 |
| 45.3465 | 0 | 4.956 | 4.914 | 0.8307 | 3.3087 | 0 | 5.1765 |
| 40.014 | 0 | 0 | 4.102 | 0.6903 | 4.3911 | 3.3649 | 3.6855 |
| 72.6165 | 7.9992 | 0 | 0.7 | 0.8307 | 1.7466 | 0 | 3.1395 |
| 68.3235 | 2.3331 | 0 | 0.882 | 0 | 2.337 | 3.9215 | 1.176 |
| 26.7165 | 0 | 0 | 2.016 | 0 | 0.861 | 0 | 11.0985 |
| 91.908 | 0 | 6.136 | 1.876 | 1.17 | 5.781 | 1.0373 | 0.3465 |
5.2问题二的模型建立与求解
对于问题二,建立随机森林分类模型,分析高钾玻璃和铅钡玻璃的分类规律;利用k-means聚类模型,对不同类型玻璃表面是否风化和其化学成分之间的关系进行划分。
5.2.1模型的建立
(1)随机森林分类模型
随机森林是以决策树为基学习器通过集成方式构建而成的有监督机器学习方法,进一步在决策树的训练过程引入了随机性,使其具备优良的抗过拟合以及抗噪能力.RF分别从样本选取和特征选择2个角度体现其随机性。
1.随机选取样本:RF中每一棵决策树的样本集均是从原始数据集中采用 Bootstrap策略有放回地抽取、重组形成与原始数据集等大的子集合。 这就意味着同一个子集里面的样本可以是重复出现的,不同子集中的样本也可以是重复出现的。
2.随机选取特征:不同于单个决策树在分割过程中考虑所有特征后,选择一个最优特征来分割节点。RF 通过在基学习器中随机考察一定的特征变量,之后在这些特征中选择最优特征。特征变量考察方式的随机性使得RF模型的泛化能力和学习能力优于个体学习器。
随机森林的算法步骤如下:
1.从原始样本集中抽取训练集。每轮从原始样本集中使用 Bootstraping 的方法抽取 n 个训练样本。共进行k轮抽取,得到k个训练集。
2.每次使用一个训练集得到一个模型,k个训练集共得到k个模型。
3.对分类问题:将上步得到的k个模型采用投票的方式得到分类结果。
以下是随机森林分类模型的流程图:
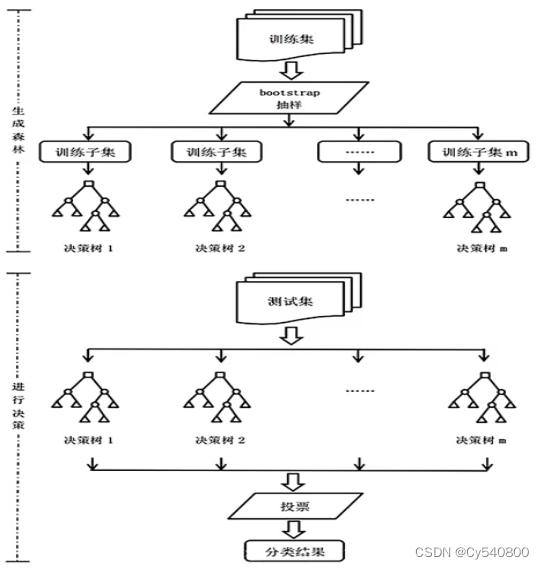
- k-means聚类分析
k-mean聚类是一种无监督学习,同时也是基于划分的聚类算法,一般用欧式距离作为衡量数据对象间相似度的指标,相似度与数据对象间的距离成反比,相似度越大,距离越小。算法需要预先指定初始聚类数目k各初始聚类中心,根据数据对象与聚类中心之间的相似度,不断更新聚类中心位置,不断降低类簇的误差平方和SSE,当其不在变化时,聚类结束,得到最终结果,适用于本题的求解。
空间中数据对象与聚类中心间的欧式距离计算公式为:
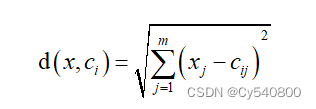 (5-5)
(5-5)
整个数据集的误差平方和SSE计算公式为:
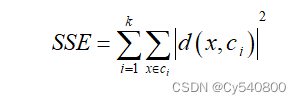 (5-6)
(5-6)
5.2.2模型求解
首先建立随机森林分类模型,分析各个化学成分含量所占的特征比重,结果如下图所示:
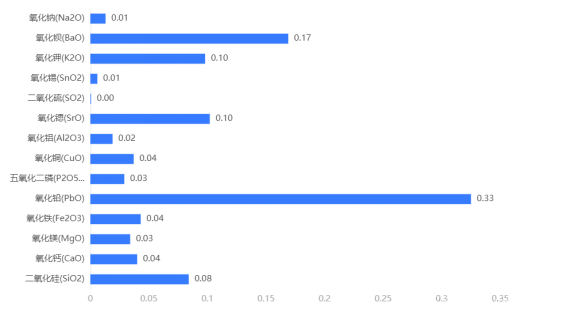
由图可知,氧化铅和氧化钡所占的特征比重较大,其中氧化铅特征比重占总成分比重的33%。因此,我们可以依据氧化铅含量的多少,来对高钾玻璃和铅钡玻璃的类型进行划分。
其次,我们对不同类型玻璃进行k-mean聚类分析,依据其化学成分含量的多少对表面是否风化进行划分。以铅钡类型为例,得到以下部分结果(由于篇幅有限,全部结果将在附录中给出):
表5-4 铅钡玻璃聚类分析表
| 聚类类别(平均值±标准差) | F | P | ||
| 类别2(n=28) | 类别1(n=22) | |||
| 表面风化 | 1.143±0.356 | 1.5±0.512 | 8.448 | 0.006*** |
| 氧化铅(PbO) | 43.448±10.93 | 18.985±7.586 | 79.813 | 0.000*** |
| 二氧化硅(SiO2) | 24.915±9.204 | 57.84±9.063 | 159.796 | 0.000*** |
| 氧化钠(Na2O) | 0.172±0.527 | 1.891±2.343 | 14.233 | 0.000*** |
| 氧化钾(K2O) | 0.163±0.336 | 0.839±3.06 | 1.354 | 0.250 |
| 氧化钙(CaO) | 2.731±1.715 | 1.466±1.787 | 6.454 | 0.014** |
| 氧化镁(MgO) | 0.602±0.671 | 0.695±0.569 | 0.274 | 0.603 |
| 氧化铝(Al2O3) | 2.62±1.498 | 5.115±3.802 | 10.103 | 0.003*** |
通过以上结果,我们可以得到大部分化学成分存在显著的差异性,故我们可以依据此进行对类型进行划分。
依据化学成分对不同类型玻璃表面风化的影响我们可以将不同类型的玻璃进行亚分类,以铅钡玻璃为例氧化铅含量越高的玻璃,其表面风化的几率越大,结果如下表(高钾类型玻璃的亚分类结果将在附录中给出):
表5-5铅钡玻璃亚分类结果图
| 聚类种类 | 表面风化 | 氧化铅(PbO) | 二氧化硅(SiO2) | 氧化钠(Na2O) | 氧化钾(K2O) | 氧化钙(CaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 氧化铁(Fe2O3) |
| 2 | 1 | 47.43 | 36.28 | 0 | 1.05 | 2.34 | 1.18 | 5.73 | 1.86 |
| 2 | 1 | 28.68 | 20.14 | 0 | 0 | 1.48 | 0 | 1.34 | 0 |
| 2 | 1 | 32.45 | 4.61 | 0 | 0 | 3.19 | 0 | 1.11 | 0 |
| 2 | 1 | 25.39 | 33.59 | 0 | 0.21 | 3.51 | 0.71 | 2.69 | 0 |
| 1 | 2 | 0.11 | 65.18 | 2.1 | 14.52 | 8.27 | 0.52 | 6.18 | 0.42 |
| 2 | 1 | 42.82 | 29.64 | 0 | 0 | 2.93 | 0.59 | 3.57 | 1.33 |
| 1 | 2 | 9.3 | 37.36 | 0 | 0.71 | 0 | 0 | 5.45 | 1.51 |
| 1 | 1 | 16.98 | 53.79 | 7.92 | 0 | 0.5 | 0.71 | 1.42 | 0 |
| 2 | 2 | 29.14 | 31.94 | 0 | 0 | 0.47 | 0 | 1.59 | 0 |
| 1 | 1 | 31.9 | 50.61 | 2.31 | 0 | 0.63 | 0 | 1.9 | 1.55 |
5.2.3合理性和灵敏度检验
为了确保模型的准确性,对模型进行合理性和灵敏度。由以上结果可知,在随机森林分类模型中氧化铅的特征比重最大,因此我们对氧化铅的含量进行增加5%和减小5%,观察其特征比重是否发生改变,对模型的灵敏性进行检验结果如下图: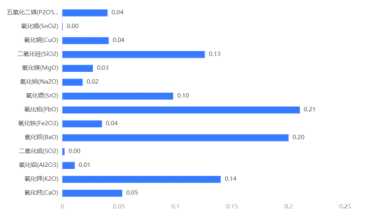

分析上图,可以看到在增加5%和减少5%后氧化铅的特征比重仍是各个化学成分比重中最大的,说明聚类效果良好,其扰动前后,特征比重变化较大,说明模型的灵敏性良好。
5.3问题三的模型建立与求解
对于问题三,在问题二的基础上利用随机森林分类模型对未知类型玻璃文物的种类进行划分,同时建立bp神经网络模型,通过两种模型的热力混淆矩阵图比较两种模型的分类情况选择结果更为准确的模型分类结果作为对本题的求解。
5.3.1数据预处理
将表单3中给出的数据,对其空缺值进行置零处理。
5.3.2模型的建立
(1)BP神经网络分类模型
BP神经网络是一种通过样本数据训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出的预测模型。在对本题结果的预测中,我们也采用了BP神经网络这一模型。
BP神经网络的基础公式为: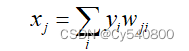
其中xj表示这种积累,yi表示某个神经元传递过来的刺激量,wji表示链接某个神经元刺激的权重,接着选取Sigmoid函数对神经元本身的输出进行激活,得到以下公式: 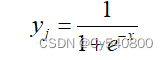
通过以上两个公式,可以分析出来BP神经网络中输出结果的计算过程。每个神经元收到刺激yj然后加权积累(权重wji)完成后产生xj,再通过激活函数产生刺激yj。
向下一层与它相连的神经元传递,依次类推最终输出结果。
接着我们通过利用向后反馈机制来修正神经元权重wji,在此用过运用了多元微分的内容,得到以下公式:
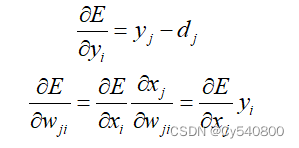
决策树分类模型
决策树是一树状结构,它从根节点开始,对数据样本进行测试,根据不同的结果将数据样本划分成不同的数据样本子集,每个数据样本子集构成——子节点 。它是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法,适用于对本题的求解中。
其中C5.0算法在决策树各级结点上选择属性时,用增益比率作为其属性的选择标准,公式如下:

5.3.3模型求解
首先利用问题二中所建立的随机森林分类模型对未知类型玻璃的类型进行分类求解,得到的结果如下:
表5-6随机森林分类预测表
| 预测结果_Y | 预测结果概率_铅钡 | 预测结果概率_高钾 | 氧化锶(SrO) | 氧化钙(CaO) | 二氧化硫(SO2) | 氧化锡(SnO2) | 氧化铅(PbO) | 氧化铁(Fe2O3) | 五氧化二磷(P2O5) | 氧化铜(CuO) | 氧化钡(BaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 二氧化硅(SiO2) |
| 高钾 | 0.13 | 0.87 | 0.03 | 6.08 | 0.51 | 0 | 0 | 2.15 | 1.06 | 2.11 | 0 | 1.86 | 7.23 | 78.45 |
| 铅钡 | 0.88 | 0.12 | 0 | 7.63 | 0 | 0 | 34.3 | 0 | 14.27 | 0 | 0 | 0 | 2.33 | 37.75 |
| 铅钡 | 0.87 | 0.13 | 0.52 | 7.19 | 0 | 0 | 39.58 | 7.06 | 2.68 | 0.21 | 4.69 | 0.81 | 2.93 | 31.95 |
| 铅钡 | 0.91 | 0.09 | 0.28 | 2.89 | 0 | 0 | 24.28 | 6.45 | 8.45 | 0.96 | 8.31 | 1.05 | 7.07 | 35.47 |
| 铅钡 | 0.94 | 0.06 | 0.21 | 1.64 | 0 | 0.49 | 12.23 | 0.81 | 0.19 | 0.94 | 2.16 | 2.34 | 12.75 | 64.29 |
| 高钾 | 0 | 1 | 0 | 0.64 | 0 | 0 | 0 | 0.27 | 0.21 | 1.73 | 0 | 0.21 | 1.52 | 93.17 |
| 高钾 | 0.07 | 0.93 | 0 | 1.12 | 0.11 | 0 | 0 | 0.24 | 0.13 | 1.17 | 0 | 0 | 5.06 | 90.83 |
| 铅钡 | 0.99 | 0.01 | 0.31 | 0.89 | 2.26 | 0 | 21.24 | 0 | 1.46 | 9.01 | 11.34 | 0 | 2.12 | 51.12 |
其次,我们利用bp神经网络分类模型和决策树分类模型对问题进行求解,得到其热力混淆矩阵图,我们将随机森林分类模型中得到的热裤混淆矩阵图与两个模型进行对比分析,如下:
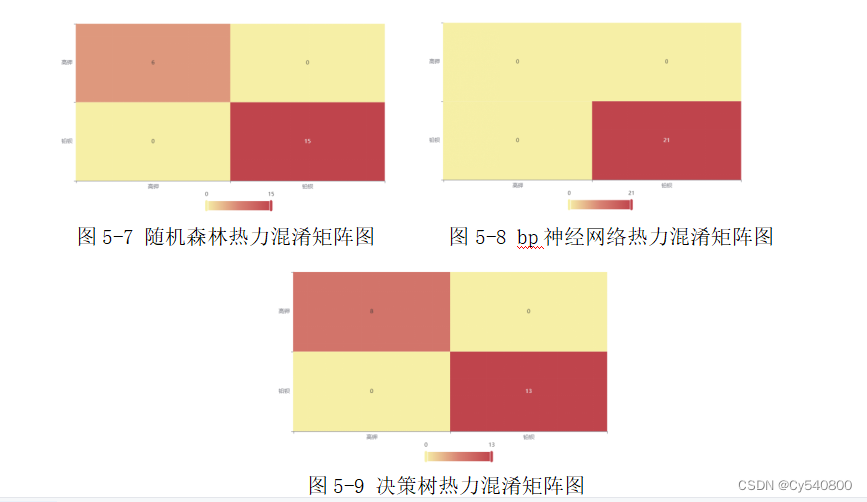
对比不同模型的分类热力混淆矩阵图可知,随机森林分类模型的分类效果更好,因此我们选择随机森林分类模型的分类结果作为最终结果结果见表5-6。
5.3.4模型灵敏度检验
同样,在问题二的基础上,对影响分类的特征比重最大的化学成分氧化铅分别增加5%和减少5%作为扰动,来对模型的灵敏度进行检验。
首先,我们对数据中的氧化铅含量整体增加5%,得到模型预测的热力混淆矩阵图:

其次,我们对数据中的氧化铅含量整体减少5%,得到模型预测的热力混淆矩阵图:

通过以上图片分析,在扰动前后对模型的分类效果产生了一定的影响,说明模型的灵敏度较高。
5.4问题四模型建立与求解
将玻璃类型分为高钾和铅钡两类,对两个类型分别化学成分之间的关系作相关性分析。
5.4.1模型的建立
相关性分析-Person相关系数
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:

上式定义了总体相关系数,常用希腊小写字母ρ作为代表符号。估算样本的协方差和标准差,可以得到皮尔逊相关系数,常用小写英文字母r表示:
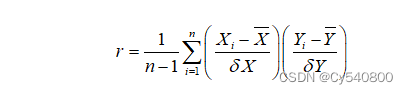
5.4.2模型的求解
首先,对于高钾类型的玻璃,利用相关性分析,分析其各化学成分之间的关系,部分结果如下(完整结果将在附录中给出):
| 二氧化硅(SiO2) | 氧化钠(Na2O) | 二氧化硫(SO2) | 氧化钡(BaO) | |
| 二氧化硅(SiO2) | 1.000(0.000***) | -0.422(0.092*) | -0.388(0.123) | -0.378(0.134) |
| 氧化钠(Na2O) | -0.422(0.092*) | 1.000(0.000***) | -0.167(0.522) | -0.184(0.480) |
| 二氧化硫(SO2) | -0.388(0.123) | -0.167(0.522) | 1.000(0.000***) | -0.232(0.370) |
| 氧化钡(BaO) | -0.378(0.134) | -0.184(0.480) | -0.232(0.370) | 1.000(0.000***) |
表5-7 高钾类型玻璃化学成分之间的相关性系数表
同时,将表格中数据进行可视化,得到其相关系数热力图,如下:
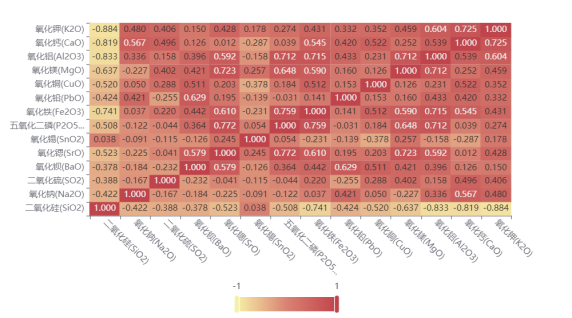
由图中的数据分析可知五氧化二磷(P2O5)和氧化锶(SrO)的相关性最强。
其次,我们对铅钡类型玻璃,利用相关性分析,分析其各化学成分之间的关系,部分结果如下(完整结果将在附录中给出):
表5-8 铅钡类型玻璃化学成分之间的相关性系数表
| 氧化钾(K2O) | 氧化钡(BaO) | 二氧化硫(SO2) | 氧化锡(SnO2) | |
| 氧化钾(K2O) | 1.000(0.000***) | -0.181(0.209) | -0.035(0.811) | -0.013(0.930) |
| 氧化钡(BaO) | -0.181(0.209) | 1.000(0.000***) | 0.630(0.000***) | -0.068(0.637) |
| 二氧化硫(SO2) | -0.035(0.811) | 0.630(0.000***) | 1.000(0.000***) | -0.069(0.632) |
| 氧化锡(SnO2) | -0.013(0.930) | -0.068(0.637) | -0.069(0.632) | 1.000(0.000***) |
同理,对得到数据进行可视化,得到其相关系数热力图,如下:
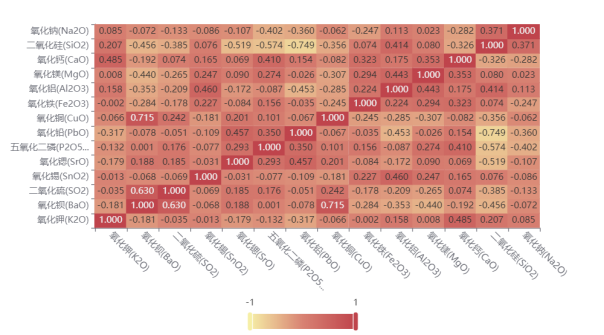
同理,由图4-2中的数据分析可知氧化钡(BaO)和氧化铜(CuO)的相关性最强。
因此,易得出不同类别之间化学成分关联关系间的差异性为:高钾玻璃化学成分间关联性最强的是五氧化二磷(P2O5)和氧化锶(SrO);而铅钡玻璃化学成分间关联性最强的是氧化钡(BaO)和氧化铜(CuO)。
- 模型的推广与评价
6.1 模型的优点
针对问题一:由于问题中的四个指标均为定类变量,因此我们采用卡方检验来进行分析;为了对比不同类型玻璃风化前后化学成分含量的变化,我们对风化前后的化学成分含量进行可视化,利用成分含量面积图,更加直观的观察其风化前后化学成分含量的变化;在预测其风化前化学成分含量时,我们采用独立样本t检验的方法,分析其风化前后的差异性,并根据其风化前各个化学成分的独立样本t检验的均值结果,作为其风化前的化学成分含量。
针对问题二:我们建立随机森林分类模型,分析各个化学成分所占总含量的特征比重,选择特征比重最大的化学成分氧化铅含量的多少作为其分类指标;分别对高钾类型和铅钡类型作k-means聚类分析,分析指标之间的差异性,以是否风化作为指标,更好的得出亚分类的划分效果;针对随机森林模型依次修改氧化铅含量的比重,得到其合理性和灵敏性。
针对问题三:在问题二的基础上,使用问题二中的随机森林分类模型进行分析,为确保预测结果的准确性,我们在这里同时采用bp神经网络分类模型,对比分析两种模型结果,选择更为准确的随机森林分类模型的结果作为其最终结果,并添加数据扰动,分析其灵敏性,确保模型的准确性和可靠性。
对于问题四:将高钾类型和铅钡类型与其各自的化学成分含量分别进行相关性分析,通过对比分析不同类型之间化学成分相关性的差异。
6.2模型的缺点
对于问题一:问题一在预测化学成分含量的精准度上可能相对较低。
对于问题二:在玻璃类型亚分类中,没有考虑颜色、纹饰等多重分类问题。
对于问题三:没有对预测结果进行验证和测试。
6.3模型的推广
对于问题一:在预测前风化问题时,可以采用线性回归模型等,计算其拟合度,进而预测各个化学元素风化前后的化学成分含量变化。
对于问题二、三:可以采用支持向量机、随机森林、神经网络等进行分类,比较各个方法的优缺点。
对于问题四:可以采用多元回归分析、主成分分析等,对成分指标进行降维,依据其主成分的贡献度,划分出主成分个数,计算每个主成分所占比重,给出主成分模型公式以及每一个主成分所包含的化学成分。
参考文献
- 干福熹.中国古代玻璃的起源和发展[J].自然杂志,2006(04):187-193+184.
- 干福熹,黄振发,肖炳荣.我国古代玻璃的起源问题[J].硅酸盐学报,1978(Z1):99-104+121-122.
- 魏志栋,贺舒敏,黄煜欣.疫情期间企业合同履行风险量化分析——基于广东省392份案例SPSS双向无序RxC表资料的卡方检验统计分析[J].西部学刊,2021(04):51-53.DOI:
- 高艺祥,杨民红,李兰会.独立样本t检验的Excel和SPSS分析[J].畜牧与饲料,2018,39(10):79-82.DOI:10.16003/j.cnki.issn1672-5190.2018.10.019.
- 王博,庄暨军,熊军,罗小臣.基于高维特征聚类优化的随机森林算法研究[J].井冈山大学学报(自然科学版),2022,43(05):52-56.
- 付贵.基于改进随机森林算法的水文监测数据异常识别研究[J].水利科技与经济,2022,28(08):76-80.
- 余峰,王珂佳,张文龙,李轶.基于遗传算法优化BP神经网络的水生态修复原位控浊混凝投药预测[J/OL].环境工程:1-12[2022-09-18].
- 张科学,吴永伟,何满潮,陈学习,姜耀东,李东,孙健东,程志恒,亢磊,王晓玲,朱俊傲,杨海江,闫星辰,尹宇航,李举然.基于蝙蝠算法优化的BP神经网络煤层冲击危险性智能综合评价研究[J/OL].现代隧道技术:1-10[2022-09-18].
- 王韶,朱姜峰.基于改进相关性分析法的配电网络单相接地故障选线[J].电力系统保护与控制,2012,40(15):76-81.
[10]杨锐.城市表层土壤重金属污染分析——对2011年全国大学生数学建模本科组A题的解答[J].科技信息,2013(04):199-200.
- 作者Sven0126,随机森林详解
https://blog.csdn.net/frankweirui/article/details/79487320,2018.3.8
附录
5.1.5
铅钡玻璃未风化前化学成分含量表:

高钾玻璃未风化前化学成分含量表:

5.2.2
铅钡类型玻璃聚类差异性表:
| 聚类类别(平均值±标准差) | F | P | ||
| 类别2(n=28) | 类别1(n=22) | |||
| 表面风化 | 1.143±0.356 | 1.5±0.512 | 8.448 | 0.006*** |
| 氧化铅(PbO) | 43.448±10.93 | 18.985±7.586 | 79.813 | 0.000*** |
| 二氧化硅(SiO2) | 24.915±9.204 | 57.84±9.063 | 159.796 | 0.000*** |
| 氧化钠(Na2O) | 0.172±0.527 | 1.891±2.343 | 14.233 | 0.000*** |
| 氧化钾(K2O) | 0.163±0.336 | 0.839±3.06 | 1.354 | 0.250 |
| 氧化钙(CaO) | 2.731±1.715 | 1.466±1.787 | 6.454 | 0.014** |
| 氧化镁(MgO) | 0.602±0.671 | 0.695±0.569 | 0.274 | 0.603 |
| 氧化铝(Al2O3) | 2.62±1.498 | 5.115±3.802 | 10.103 | 0.003*** |
| 氧化铁(Fe2O3) | 0.68±0.87 | 0.615±1.04 | 0.057 | 0.812 |
| 氧化铜(CuO) | 2.415±2.992 | 1.161±1.243 | 3.394 | 0.072* |
| 氧化钡(BaO) | 12.377±9.949 | 7.613±4.819 | 4.247 | 0.045** |
| 五氧化二磷(P2O5) | 4.916±4.253 | 1.076±1.878 | 15.503 | 0.000*** |
| 氧化锶(SrO) | 0.442±0.269 | 0.215±0.199 | 10.947 | 0.002*** |
| 氧化锡(SnO2) | 0.047±0.138 | 0.07±0.281 | 0.147 | 0.704 |
铅钡类型玻璃聚类结果表:
| 聚类种类 | 表面风化 | 氧化铅(PbO) | 二氧化硅(SiO2) | 氧化钠(Na2O) | 氧化钾(K2O) | 氧化钙(CaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 氧化铁(Fe2O3) |
| 2 | 1 | 47.43 | 36.28 | 0 | 1.05 | 2.34 | 1.18 | 5.73 | 1.86 |
| 2 | 1 | 28.68 | 20.14 | 0 | 0 | 1.48 | 0 | 1.34 | 0 |
| 2 | 1 | 32.45 | 4.61 | 0 | 0 | 3.19 | 0 | 1.11 | 0 |
| 2 | 1 | 25.39 | 33.59 | 0 | 0.21 | 3.51 | 0.71 | 2.69 | 0 |
| 1 | 2 | 0.11 | 65.18 | 2.1 | 14.52 | 8.27 | 0.52 | 6.18 | 0.42 |
| 2 | 1 | 42.82 | 29.64 | 0 | 0 | 2.93 | 0.59 | 3.57 | 1.33 |
| 1 | 2 | 9.3 | 37.36 | 0 | 0.71 | 0 | 0 | 5.45 | 1.51 |
| 1 | 1 | 16.98 | 53.79 | 7.92 | 0 | 0.5 | 0.71 | 1.42 | 0 |
| 2 | 2 | 29.14 | 31.94 | 0 | 0 | 0.47 | 0 | 1.59 | 0 |
| 1 | 1 | 31.9 | 50.61 | 2.31 | 0 | 0.63 | 0 | 1.9 | 1.55 |
高钾类型玻璃聚类差异性表:
| 聚类类别(平均值±标准差) | F | P | ||
| 类别1(n=9) | 类别2(n=8) | |||
| 表面风化 | 1.667±0.5 | 1.0±0.0 | 14.118 | 0.002*** |
| 氧化钾(K2O) | 1.986±3.22 | 10.355±2.054 | 39.566 | 0.000*** |
| 二氧化硅(SiO2) | 89.663±7.119 | 63.43±3.752 | 86.74 | 0.000*** |
| 氧化钠(Na2O) | 0.0±0.0 | 0.78±1.451 | 2.623 | 0.126 |
| 氧化钙(CaO) | 1.327±1.419 | 6.125±2.717 | 21.575 | 0.000*** |
| 氧化镁(MgO) | 0.437±0.593 | 1.21±0.675 | 6.326 | 0.024** |
| 氧化铝(Al2O3) | 2.764±1.67 | 7.495±2.463 | 21.938 | 0.000*** |
| 氧化铁(Fe2O3) | 0.44±0.735 | 2.549±1.584 | 12.905 | 0.003*** |
| 氧化铜(CuO) | 1.492±1.136 | 3.038±1.52 | 5.726 | 0.030** |
| 氧化铅(PbO) | 0.139±0.333 | 0.448±0.673 | 1.49 | 0.241 |
| 氧化钡(BaO) | 0.219±0.657 | 0.651±1.044 | 1.072 | 0.317 |
| 五氧化二磷(P2O5) | 0.533±0.451 | 1.714±1.658 | 4.244 | 0.057* |
| 氧化锶(SrO) | 0.008±0.023 | 0.049±0.055 | 4.192 | 0.059* |
| 氧化锡(SnO2) | 0.262±0.787 | 0.0±0.0 | 0.882 | 0.362 |
| 二氧化硫(SO2) | 0.0±0.0 | 0.152±0.213 | 4.667 | 0.047** |
高钾类型玻璃聚类结果表:
| 聚类种类 | 表面风化 | 氧化钾(K2O) | 二氧化硅(SiO2) | 氧化钠(Na2O) | 氧化钙(CaO) | 氧化镁(MgO) | 氧化铝(Al2O3) | 氧化铁(Fe2O3) | 氧化铜(CuO) |
| 2 | 1 | 9.99 | 69.33 | 0 | 6.32 | 0.87 | 3.93 | 1.74 | 3.87 |
| 1 | 1 | 5.19 | 87.05 | 0 | 2.01 | 0 | 4.06 | 0 | 0.78 |
| 2 | 1 | 12.37 | 61.71 | 0 | 5.87 | 1.11 | 5.5 | 2.16 | 5.09 |
| 2 | 1 | 9.67 | 65.88 | 0 | 7.12 | 1.56 | 6.44 | 2.06 | 2.18 |
| 2 | 1 | 10.95 | 61.58 | 0 | 7.35 | 1.77 | 7.5 | 2.62 | 3.27 |
| 2 | 1 | 7.37 | 67.65 | 0 | 0 | 1.98 | 11.15 | 2.39 | 2.51 |
| 2 | 1 | 7.68 | 59.81 | 0 | 5.41 | 1.73 | 10.05 | 6.04 | 2.18 |
| 1 | 2 | 0 | 92.63 | 0 | 1.07 | 0 | 1.98 | 0.17 | 3.24 |
| 1 | 2 | 0.59 | 95.02 | 0 | 0.62 | 0 | 1.32 | 0.32 | 1.55 |
| 1 | 2 | 0.92 | 96.77 | 0 | 0.21 | 0 | 0.81 | 0.26 | 0.84 |
5.3.3
bp神经网络分类预测结果表:
| 预测结果_Y | 预测结果概率_铅钡 | 预测结果概率_高钾 | 二氧化硅(SiO2) | 氧化钾(K2O) | 氧化钠(Na2O) | 氧化钙(CaO) | 氧化镁(MgO) | 二氧化硫(SO2) | 氧化铝(Al2O3) | 氧化铜(CuO) | 氧化铁(Fe2O3) | 氧化锡(SnO2) | 氧化铅(PbO) | 氧化钡(BaO) |
| 高钾 | 0.0006008220283589827 | 0.999399177971641 | 78.45 | 0 | 0 | 6.08 | 1.86 | 0.51 | 7.23 | 2.11 | 2.15 | 0 | 0 | 0 |
| 铅钡 | 1 | 9.986133481415243e-21 | 37.75 | 0 | 0 | 7.63 | 0 | 0 | 2.33 | 0 | 0 | 0 | 34.3 | 0 |
| 铅钡 | 0.9999999998029364 | 1.9706359132935406e-10 | 31.95 | 1.36 | 0 | 7.19 | 0.81 | 0 | 2.93 | 0.21 | 7.06 | 0 | 39.58 | 4.69 |
| 铅钡 | 0.9999999989568417 | 1.0431583900707858e-9 | 35.47 | 0.79 | 0 | 2.89 | 1.05 | 0 | 7.07 | 0.96 | 6.45 | 0 | 24.28 | 8.31 |
| 高钾 | 0.11927022657318354 | 0.8807297734268165 | 64.29 | 0.37 | 1.2 | 1.64 | 2.34 | 0 | 12.75 | 0.94 | 0.81 | 0.49 | 12.23 | 2.16 |
| 高钾 | 0.0000017096202509225833 | 0.9999982903797491 | 93.17 | 1.35 | 0 | 0.64 | 0.21 | 0 | 1.52 | 1.73 | 0.27 | 0 | 0 | 0 |
| 高钾 | 0.000006318172599217853 | 0.9999936818274008 | 90.83 | 0.98 | 0 | 1.12 | 0 | 0.11 | 5.06 | 1.17 | 0.24 | 0 | 0 | 0 |
| 铅钡 | 0.6130509769332575 | 0.38694902306674256 | 51.12 | 0.23 | 0 | 0.89 | 0 | 2.26 | 2.12 | 9.01 | 0 | 0 | 21.24 | 11.34 |
决策树分类预测结果表:
| 预测结果_Y | 预测结果概率_铅钡 | 预测结果概率_高钾 | 氧化锡(SnO2) | 二氧化硫(SO2) | 氧化铜(CuO) | 五氧化二磷(P2O5) | 氧化锶(SrO) | 氧化钡(BaO) | 氧化铅(PbO) | 氧化铁(Fe2O3) | 氧化镁(MgO) | 氧化铝(Al2O3) | 氧化钾(K2O) | 氧化钙(CaO) |
| 高钾 | 0 | 1 | 0 | 0.51 | 2.11 | 1.06 | 0.03 | 0 | 0 | 2.15 | 1.86 | 7.23 | 0 | 6.08 |
| 铅钡 | 1 | 0 | 0 | 0 | 0 | 14.27 | 0 | 0 | 34.3 | 0 | 0 | 2.33 | 0 | 7.63 |
| 铅钡 | 1 | 0 | 0 | 0 | 0.21 | 2.68 | 0.52 | 4.69 | 39.58 | 7.06 | 0.81 | 2.93 | 1.36 | 7.19 |
| 铅钡 | 1 | 0 | 0 | 0 | 0.96 | 8.45 | 0.28 | 8.31 | 24.28 | 6.45 | 1.05 | 7.07 | 0.79 | 2.89 |
| 铅钡 | 1 | 0 | 0.49 | 0 | 0.94 | 0.19 | 0.21 | 2.16 | 12.23 | 0.81 | 2.34 | 12.75 | 0.37 | 1.64 |
| 高钾 | 0 | 1 | 0 | 0 | 1.73 | 0.21 | 0 | 0 | 0 | 0.27 | 0.21 | 1.52 | 1.35 | 0.64 |
| 高钾 | 0 | 1 | 0 | 0.11 | 1.17 | 0.13 | 0 | 0 | 0 | 0.24 | 0 | 5.06 | 0.98 | 1.12 |
| 铅钡 | 1 | 0 | 0 | 2.26 | 9.01 | 1.46 | 0.31 | 11.34 | 21.24 | 0 | 0 | 2.12 | 0.23 | 0.89 |
5.4.2
高钾类型相关性分析python代码:
import pandas as pd
data = pd.read_excel("工作簿1_版本1_空值处理.xlsx")
df = data.iloc[:20,:]
corr=df.corr()
print(df.corr())
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.family']=['sans-serif']
plt.rcParams['font.sans-serif']=['SimHei']
heatmap=sns.heatmap(corr)
plt.show()
铅钡类型性关系分析python代码:
import pandas as pd
data = pd.read_excel("工作簿3_版本1_空值处理.xlsx")
df = data.iloc[:20,:]
corr=df.corr()
print(df.corr())
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.family']=['sans-serif']
plt.rcParams['font.sans-serif']=['SimHei']
heatmap=sns.heatmap(corr)
plt.show()
这篇关于2022全国大学生数学建模大赛C题——古代玻璃制品的成分分析与鉴别的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






