本文主要是介绍关系的性质(自反,反自反,对称,反对称,传递),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
自反
若∀a∈A,必有<a,a>∈R,则称R是自反的,(关系矩阵对角线都为1)。
例:A={1,2,3},R={<1,1,>,<2,2>,<3,3>

反自反
若∀a∈A,必有<a,a>R,则称R是反自反的
例:A={1,2,3},R={<1,2,>,<1,3>,<2,1,>,<2,3>,<3,1>,<3,2>}
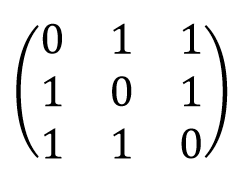
对称
若<a,b>∈R,必有<b,a>∈R,则称R是对称的,(关系矩阵rij=rji,即为对称矩阵)
例: A={1,2,3},R={<1,2>,<2,1>,<1,1>,<2,2>} R={<1,3>,<3,1,>,<2,3>,<3,2>}
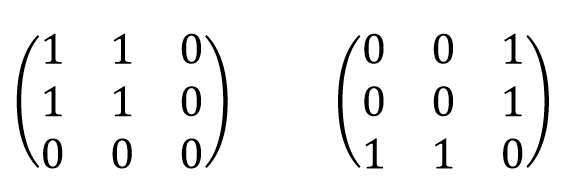
反对称
若<a,b>∈R,必有<b,a>∈R,则称R是反对称的(关系矩阵rij和rji不能同时为1,即关于对角线对称的元素不能同时为1)
例: A={1,2,3},R={<1,2>,<1,3>} R={<1,2>,<2,3>,<3,1>}
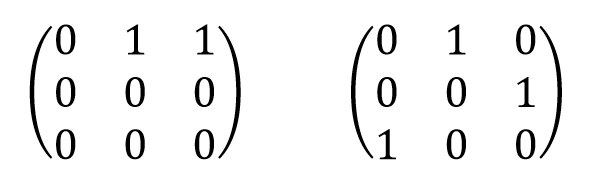
传递
若<a,b>∈R、<b,c>∈R,必有<a,c>∈R,则称R是传递的
例: A={1,2,3},R={<1,2>,<2,3>,<1,3>}
试题
给定A:{1,2,3,4},考虑A上的关系R,若R={<1,3>,<1,4>,<2,3>,<2,4>,<3,4>,<4,4>},则R是( )
A:自反的
B:对称的
C:传递的
D:反自反的
【答案】C
设集合A={a,b,c,d},现有A上的二元关系R={<a,b>,<b,c>,<c,b>,<b,a>},则A是( )
A:自反的
B:对称的
C:反对称的
D:传递的
【答案】B
下列关于整数集合上的整除关系描述不正确的是( )
A:自反的
B:对称的
C:反对称的
D:传递的
【答案】B,自反的、反对称的(2能整除4,4不能整除2)、传递的(2能整除4,4能整除8,2一定能整除8)
设R={<1,3>,<1,4>,<2,3>,<3,1>,<3,4>,<4,2>}是A={1,2,3,4}上的关系,说明R是否具有自反、反自反、对称、反对称性质。
【答案】<1,1>,<2,2,>,<3,3>,<4,4>都∉R,所以R是反自反的,不是自反的
<1,4>∈R,<4,1>∉R,所以R不是对称的
<1,3>∈R,<3,1>∈R,所以R不是反对称的
这篇关于关系的性质(自反,反自反,对称,反对称,传递)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






