本文主要是介绍吴恩达深度学习_第一课(3)《浅层神经网络》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
神经网络概览
符号变化
变量上标是圆括号 (1),(2),(3)…(i) 表示第 i 个样本的数据:x(1),x(2)…
变量上标是方括号[1],[2],[3]…[i] 表示第 i 层layer的数据:x[1],x[2]…
举个例子:

x作为输入进入第一层,配合W[1]和b[1]进行计算,得到第一层结果a[1];a[1]作为第二层的输入,配合W[2]和b[2]进行计算,得到第二层结果a[2],并计算本次前向传播的损失函数。
类似于单层逻辑回归中的反向传播需要计算dz和da
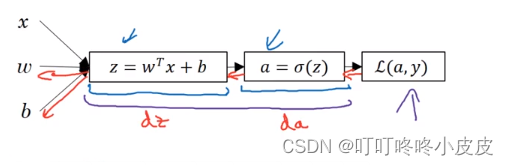
在神经网络中,根据对某层参数w和b的偏导,也有dz[2],da[2],dw[2],db[2]

神经网络表示
神经元结构
单个结点中包含当前层的w和b,并在本结点内使用激活函数激活输出值。
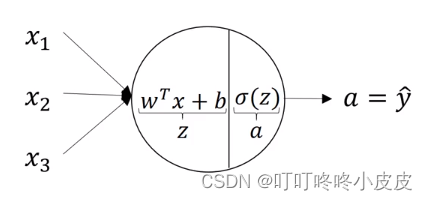
神经网络结构
神经网络大体主要有输入层、隐藏层、输出层。
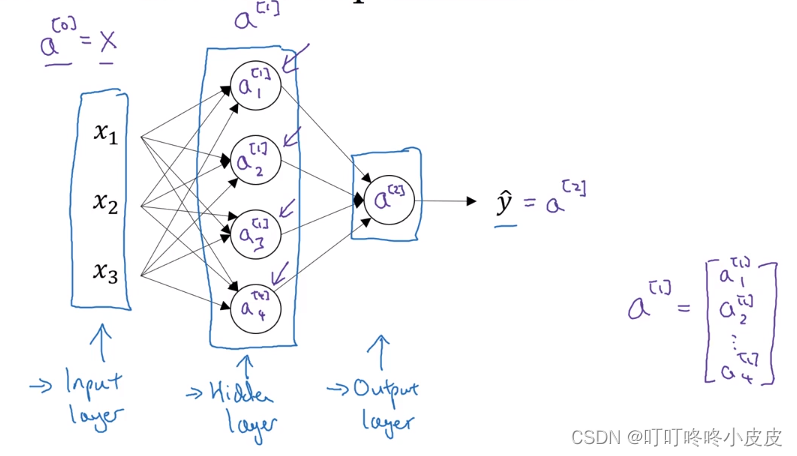
输入层的向量x,即激活值(第0层作为输入,没有激活函数)可以写成a[0]
隐藏层的激活值为a[1],例如这里的四个节点,分别记作a1[1],a2[1],a3[1],a4[1],类似右边这个4维矩阵的存储形式
隐藏层输出值作为输出层的输入值,激活后的激活值为a[2],等于预测值 y ^ \widehat{y} y
通常输入层(第0层)不计入总层数,因此,上图为2层网络
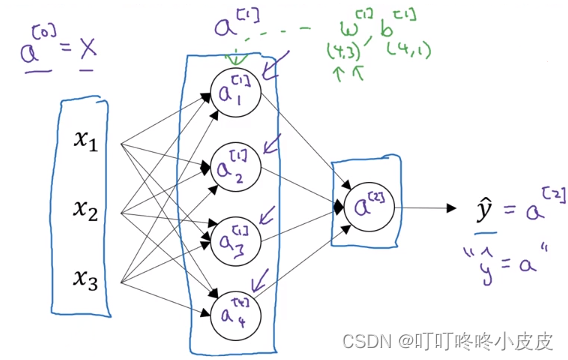
这里w[1].shape是(4,3),其中4是因为有4个隐藏单元,3是因为有3个输入特征。
计算神经网络的前向输出
神经元在第1层运算本层激活值的运算:
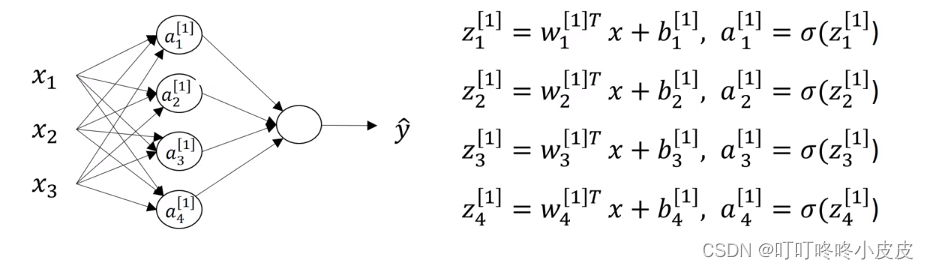
具体维度运算:
思想:当某层有多个结点时,纵向堆叠本层结点的运算结果:Z,a
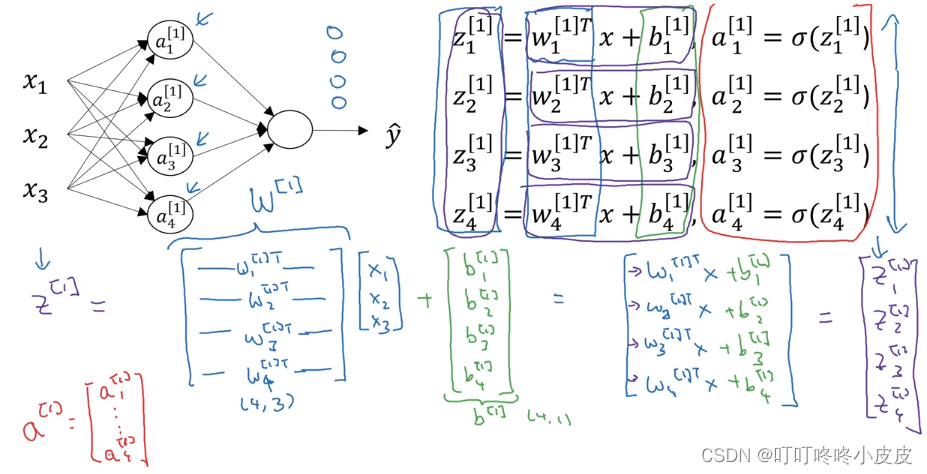
(4,3)的原因:因为x有三个变量x1,x2,x3,所以w也是(3,1)列向量,为了能点乘需要w.T(1,3),又因为w[1]是w1,w2,w3,w4竖着拼起来组合,所以w[1]是(4,3)
在手写的表示中,W[1]使用大写W,而不是w。已经默认为参数向量转置再拼起来组成的矩阵,不需要类似w加上转置符号写成W[1] T
- 下图右侧列出本网络两层结构的公式。
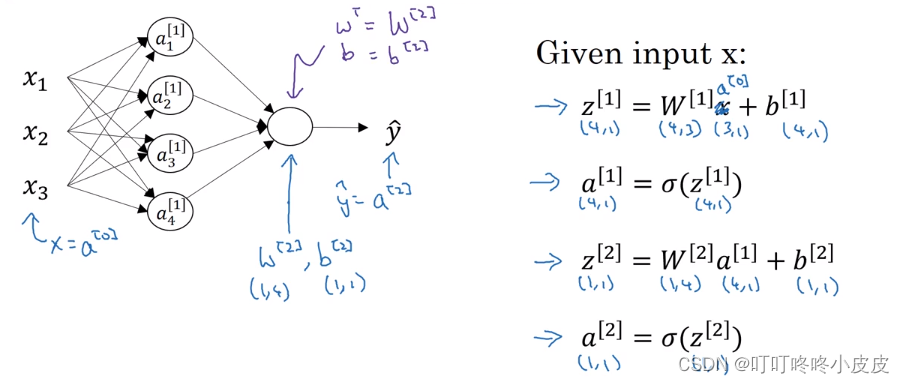
W[1]是内部转置的(4,3)矩阵,最终输出为a[1](4,1)。
因为第2层只有一个结点,输入4个参数,所以W[2]在内部对w(4,1)转置,得到W[2](1,4),计算得到z[2](1,1),最终输出 y ^ \widehat{y} y =a[2](1,1)
单个样本向下一层传输时,输出尽量调整为纵向形式,也方便下一层直接使用纵向形式。
多个样本尽量将单个样本横着拼成一个矩阵,包括输出也尽量横着拼,类似上周作业里面的样本矩阵 X_train:(12288,209)
多个样本的向量化
列出所有情况及符号说明
若有m个样本,会产生m个预测值 y ^ \widehat{y} y ,下面紫色标记解释a[2](i)的意义:方括号是第2层,圆括号是第i个样本
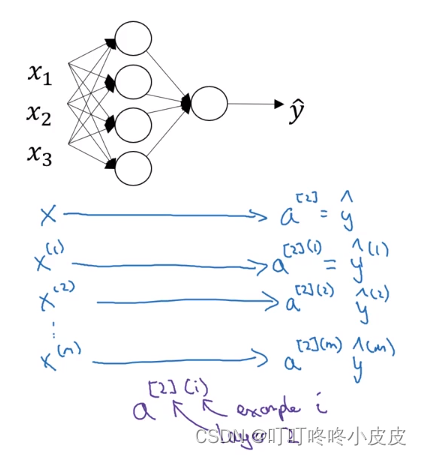
向量化处理
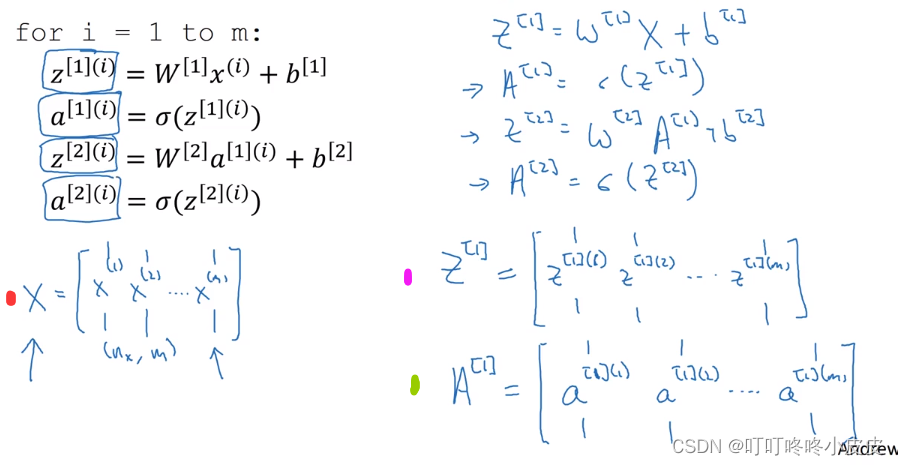
红色输入矩阵X中,将图片所有像素值nx纵向排列形成单个样本的输入值,将不同样本的输入值x(1),x(2)…横向拼成矩阵X
紫色输出矩阵Z[1]代表第1层隐藏层的输出,每一列代表某单个样本在第1层的输出结果,多个样本的输出结果向量z[1](1),z[1](2)横向拼接成矩阵Z
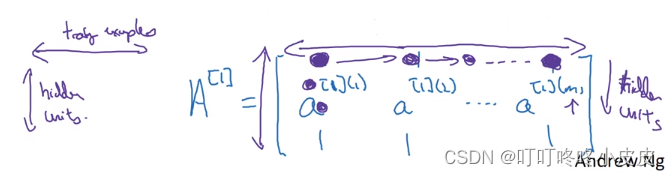
绿色激活值矩阵A[1]代表第1层隐藏层的激活值输出,每一列a[1](1),a[1](2)…分别代表某单个样本的激活值,每列的激活值横向拼成矩阵A
横向是训练样本training example,纵向是隐藏层单元hidden unit
以线代中的矩阵为例,矩阵中[0][0]位置的值是第1个样本经过第1隐藏层的第1个神经元的激活值;[1][0]位置的值是第1个样本经过第1隐藏层的第2个神经元的激活值;[0][1]位置的值是第2个样本经过第1隐藏层的第1个神经元的激活值…
向量化实现的解释
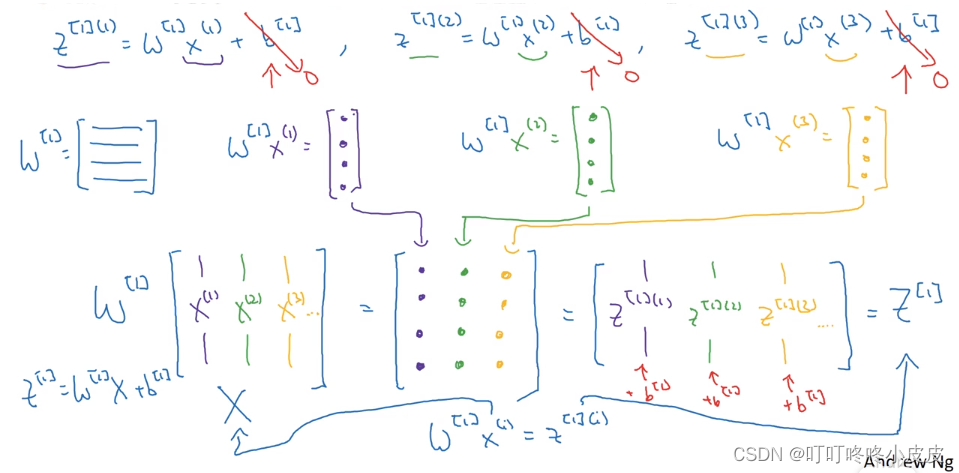
下图表示在第1隐藏层,各样本输出的向量表示。(别忘了 W[1]里面是已经转置过的参数w向量)
激活函数
为什么需要激活函数
如果使用线性激活函数,神经网络只是把输入线性组合进行输出,无论多深,都只是进行线性计算,会导致隐藏层失效,成为最简单的逻辑回归函数。
通常使用线性激活函数的地方是输出层
常用激活函数
在之前惯用sigmoid函数的隐藏层和输出层,可以使用别的函数,可以是非线性函数。

通常使用g(z)表示,并且可以用g[1],g[2]…区别不同层的激活函数。
tanh函数:类似将sigmoid函数简单平移,但是几乎所有场合都比sigmoid更加优越,因为平均值更加接近0,更便于后续运算。tanh与sigmoid共有缺点:当z极大/极小,斜率趋于0,拖慢梯度下降
ReLU函数:在输入是负值的情况下,使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解过拟合。是最常用的激活函数
一些经验:
- 输出为0 / 1,仅在二元分类,sigmoid函数适合作为输出层激活函数,其他时候几乎不用
- 不确定隐藏层用哪个,使用ReLU
神经网络的梯度下降
回顾一下大致思想:计算预测值,计算损失函数及成本函数,计算偏导,梯度下降更新参数…循环往复 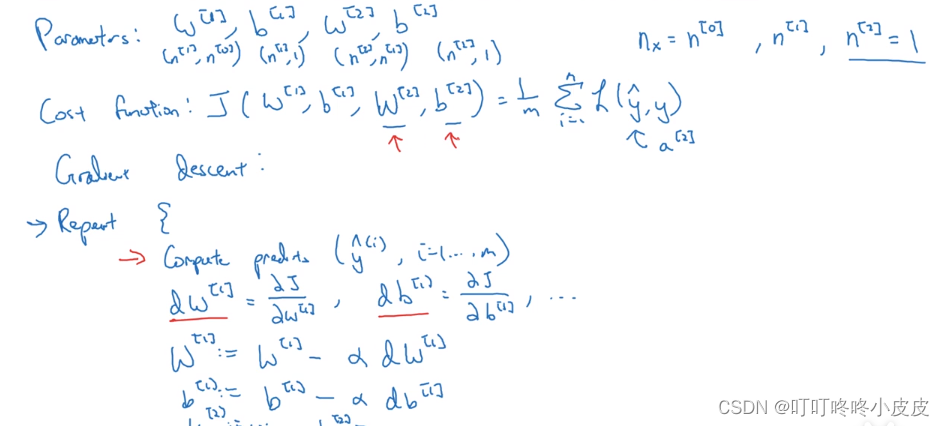
分为前向传播,反向传播。正向传播容易分析,反向传播的导数公式推导可看可不看。
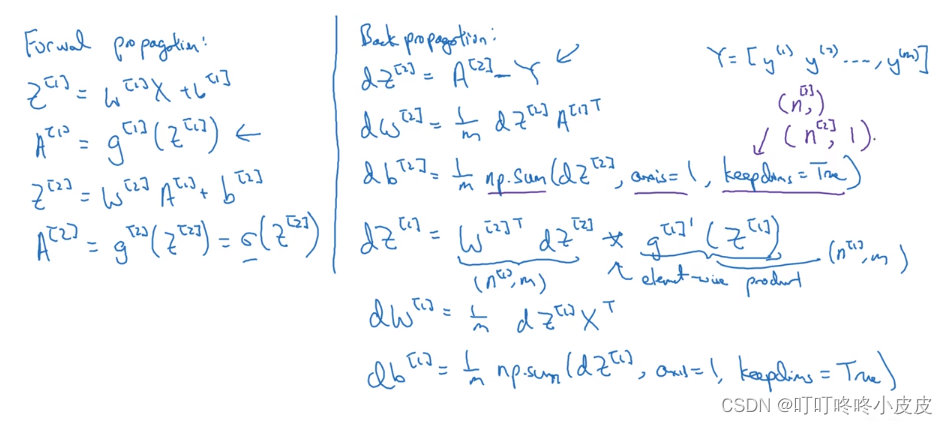
公式推导:类似逻辑回归,需要推导da[2],dz[2],db[2],dw[2],da[1],db[1],dz[1],dw[1]这些导数值。

左侧da[1],dz[1]的链式推导如下(省略等式右边的偏导符号;没有考虑矩阵,所以没有转置):

另外的dw[1],db[1] 直接类似 dw[2],db[2]求法即可。

至于为什么dz[1]中的w[2]要转置,是因为w[2]维度是(n[2],n[1]),dz[2]维度和z[2]维度一致,都是(n[2],m),z[1]维度也是(n[1],m)。因此对w[2]进行转置。(维度原因参考下一周课程)
随机初始化
神经网络中若参数矩阵初始化为0,会导致梯度下降失效
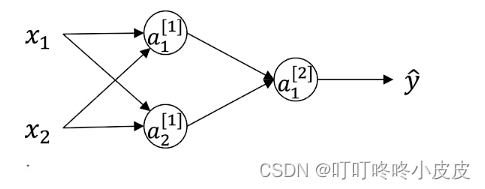
第一隐藏层的w和b都被初始化为0,会导致计算出来a1和a2相等,翻过来导致两个第一隐藏层单元 对 第二隐藏层输出单元的影响一致,且永远一致,无法体现多个隐藏单元的效果。导致退化为多层单个神经元网络。
对于上面这个网络的正确做法:
w1=np.random.radn((2,2))*0.01
b1=np.zero((2,1))
w2=np.random.radn((1,2))*0.01
b2=0
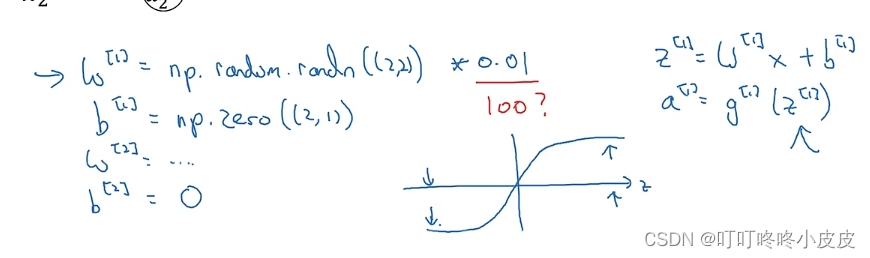
使用乘0.01是为了防止梯度消失/梯度爆炸
数据线性可分/不可分
所谓可分是指可以没有误差地分开
简单的说就是如果用一个线性函数可以将两类样本完全分开,就称这些样本是线性可分的。
比如二维空间中的直线、三维空间中的平面以及高维空间中的线性函数
判断是否线性可分:
不同样本集用凸包包起来,判断不同凸包的边是否有交叉。(凸包概念:如果给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集合中所有的点。)
这篇关于吴恩达深度学习_第一课(3)《浅层神经网络》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




