【笔记】神经网络——Rita_Aloha

2023-10-07 22:49
文章标签 笔记 神经网络 aloha rita

本文主要是介绍【笔记】神经网络——Rita_Aloha，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）

一、神经元

1.M-P模型

图中，xᵢ(i=1,2,...,n)表示来自与当前神经元项链的其他神经元传递的输入信号，w~ij~表示从神经元i到神经元j的连接强度或权值，θ~j~表示神经元j的激活阈值或偏置，f表示激活函数或转移函数。神经元的输出x~j~可以表示为如下形式：

2.学习规则

  • Hebb学习规则：如果两个神经元在同一时刻被激发，则它们之间的联系应该被强化。

    其中，w~ij~(t+1)和w~ij~(t)分别表示在t+1和t时刻时神经元j与神经元i之间的连接强度，y~i~和y~j~分别为神经元i和j的输出。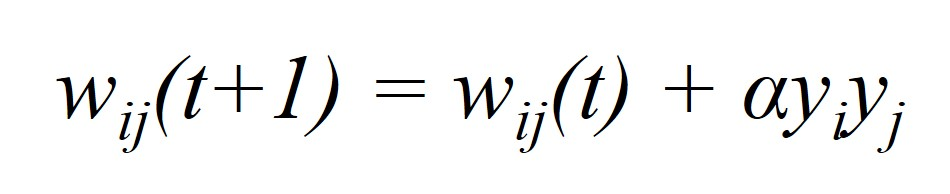
  • 有监督Delta学习规则：通过对连接权值进行不断调整以使神经元的实际输出和期望输出到达一致。

    其中，α表示算法的学习速率，d~i~和y~i~表示神经元i的期望输出和实际输出，x~j~(t)表示神经元j在t时刻的状态（激活或抑制）。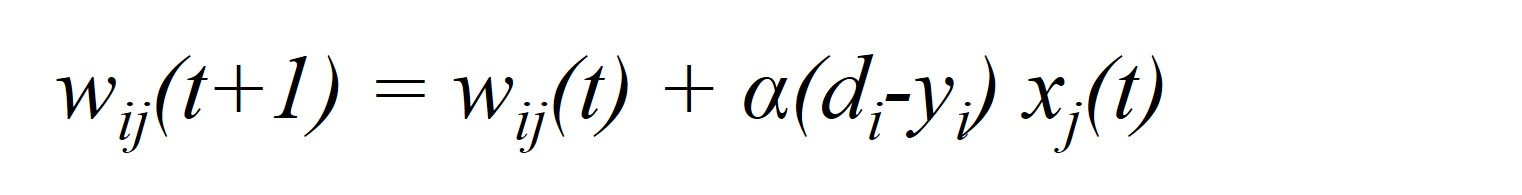

二、感知机（Perception）

输出公式可以改写成：g(W * a) = z。这个公式就是神经网络中从前一层计算后一层的矩阵运算。

三、Hopfield神经网络模型（离散型网络DHNN，Discrete Hopfield Neural Network）

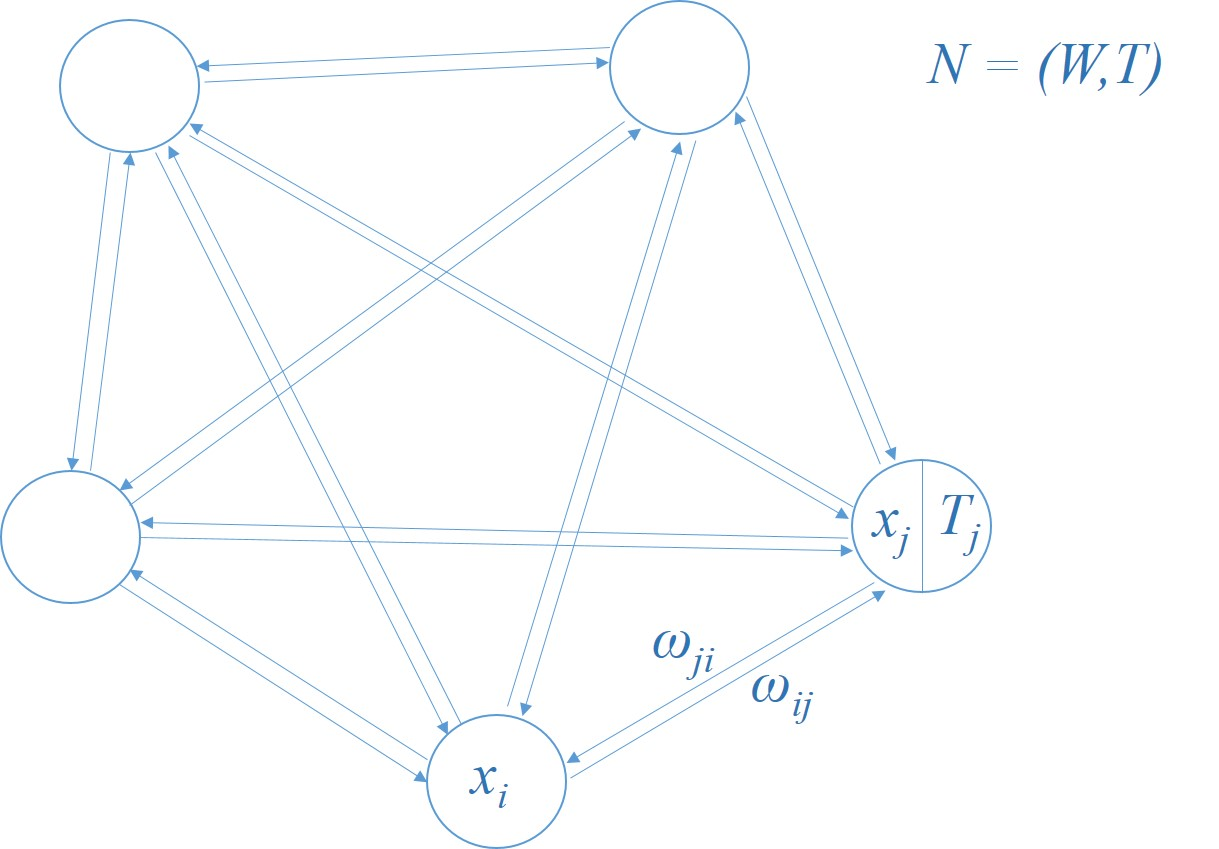
1.网络的状态

这是单层全反馈网络，共有n哥神经元。DHNN网络可简记为N=(W,T)。反馈网络的初始状态为X(0)=[x~1~(0),x~2~(0),...,x~n~(0)]^T^，反馈网络状态为X=[x~1~,x~2~,...,x~n~]^T^。其中，每一个神经元的状态变化：

对于DHNN一般ω~ii~=0，ω~ij~=ω~ji~

2.异步工作方式

网络运行时每次只有一个神经元进行转态更新，其他神经元的状态权值不变。神经元转态顺序可以预先设定，也可以随机选定。

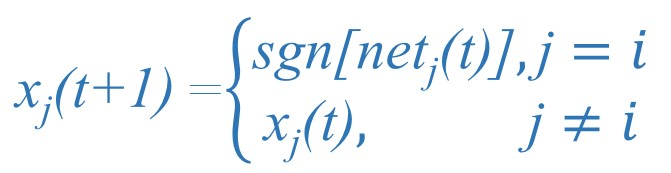
3.同步工作方式

所有神经元同时转态，即：

4.吸引子的定义与定理

【定义】若网络状态X满足X=f(W~T~x-T)，则称X为网络的吸引子

【定理】对于DHNN网络，若按照异步方式调整网络状态，且连接权矩阵W为对称阵，则对于任意初态网络都最终收敛于一个吸引子中。

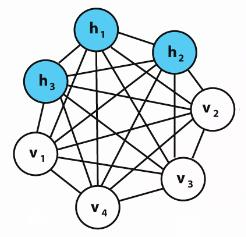
四、玻尔兹曼机（Boltzmann Machine，BM）

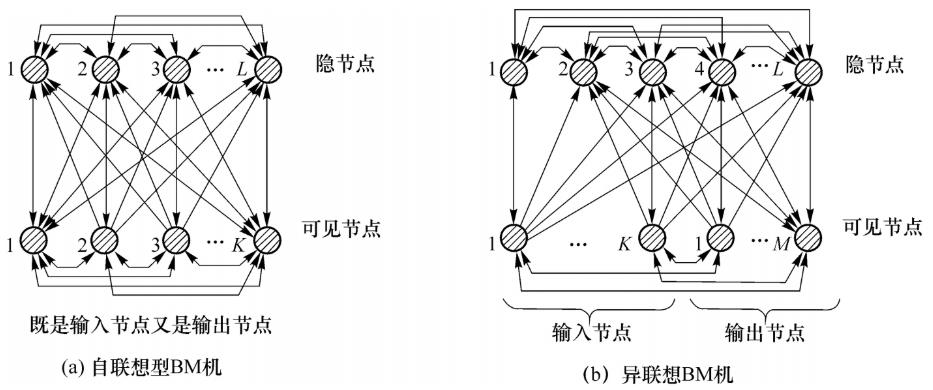
BM的节点分为可见节点与隐节点，所有的节点全连接。

1.网络原理

BM机是在Hopfield神经网络模型基础上融入模拟退火法。它保持了Hopfield神经网络模型的假设（权重对称；自身无连接；二值输出），选择模拟退火算法（先采用较大的温度系数及进行粗调，然后逐渐减小温度系数进行微调），达到让每一个神经元按照一定的概率分布转态的目的，来避免陷入局部最优解。

2.网络状态

五、受限玻尔兹曼机（Restricted BM，RBM）

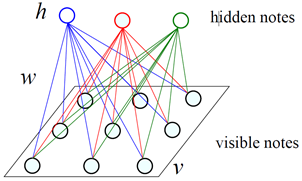
1.网络结构模型

RBM是在玻尔兹曼机的基础上更加调整，其中保持了玻尔兹曼机的部分特征（由可见层和隐藏层构成；信息可双向流动），同时去掉了层内单元之间的连接，即层间全连接，层内无连接。

记 θ=(W,a,b) 表示RBM中的参数。

正向传播：可见层已知，利用权重和偏置根据随机概率（σ是随机概率）采样出隐藏层，采样概率为

反向传播：隐藏层已知，利用权重和对应偏置采样出可见层，采样概率为

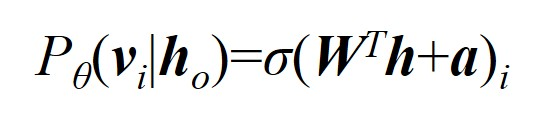
2.Gibbs采样

3.对比散度（Contrastive Divergence，CD）算法

4.算法总结

注意：

  • 当k=1时，参数更新以在线学习的方式进行
  • 一般，权重矩阵W可初始化为来自正态分布N(0,0.01)的随机数；隐藏层偏置b初始化为0；可见层偏置a初始化为a~i~=log[p~i~/(1-p~i~)]，其中p~i~表示训练样本中第i个特征处于激活状态（即取值为1）的样本所占的比例
  • 学习率η较大时收敛速度更快，但可能引起算法不稳定；而η较小时，收敛速度变慢。因此，可在参数更新式中加入动量项θ:=ρθ+η[∂lnL~θ,s~/∂θ]，其中ρ为动量项学习率
  • CD-k算法中的参数k通常取得很小，实际应用中甚至取k=1

六、反向传播算法（Back Propagation，BP）

1.前向传播与后向传播

前向传播算法主要用于计算输出结果；后向传播算法主要用于计算输出结果与实际结果之间的误差。因此，神经网络就是通过前向传播与后向传播的循环迭代来训练模型。

反向传播算法的主要思想是通过梯度下降的方法调节参数，进而训练模型。

2.logistic函数

输出是有限离散的情况下，预测行为即是分类行为。线性分类器的目的就是找到一个可以将两类样本分开的超平面【ω^T^x+b=0】。对于logistic回归一般公式为g(z)=1/[1+e^-z^]。当x为n维的样本时，对于logistic回归有：

由此可以得到logistic回归的对数似然损失函数（cost function）

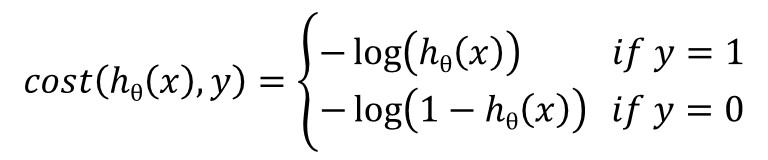
将以上两个表达式合并，则单个样本的损失函数为

全体样本的损失函数可以表示为

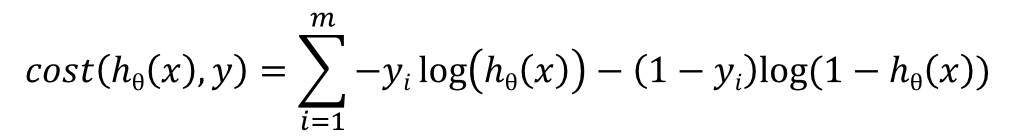
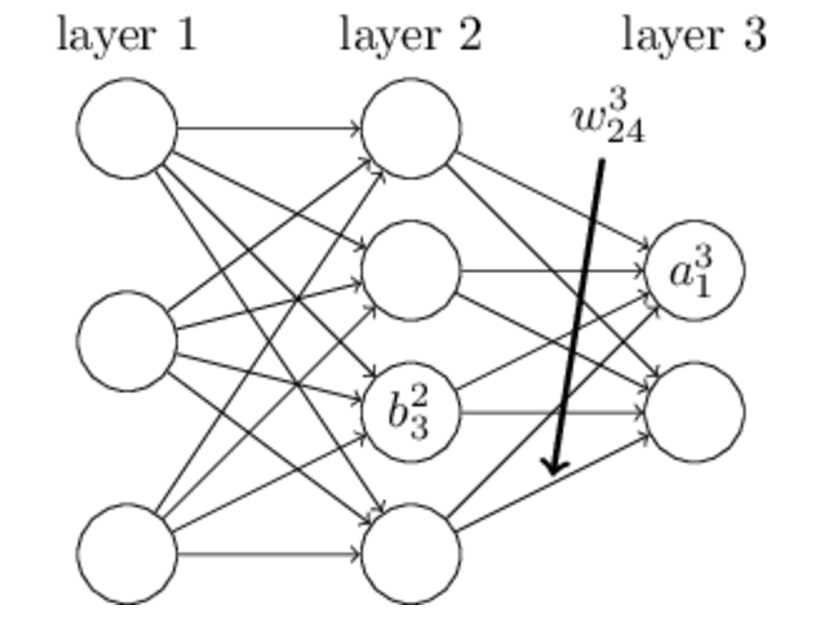
3.网络变量定义

4.反向传播算法的四个基本方程

【Hadamard积⊙：两个同阶矩阵中对应元素的乘积，称为元素对应乘积(element-wise product)或者Hadamard乘积(Hadamard product)，记为\large A\bigodot B。】

⑴输出层误差

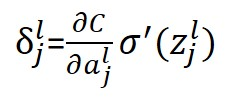
即

其中σ'为对sigmoid函数的偏导，C为Cost函数

⑵下一层误差变化引起当前层误差的变化方程

⑶代价函数与偏置

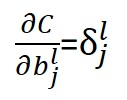
⑷代价函数与权重

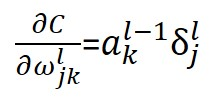
5.反向传播算法实现(神经网络训练流程)

七、径向基神经网络（RBF）

1.径向基核函数

（1）理解RBF网络的工作原理可从两种不同的观点出发：

①当用RBF网络解决非线性映射问题时，用函数逼近与内插的观点来解释，对于其中存在的不适定(illposed）问题，可用正则化理论来解决；

②当用RBF网络解决复杂的模式分类任务时，用模式可分性观点来理解比较方便，其潜在合理性基于Cover关于模式可分的定理。

（2）所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心x~c~之间欧氏距离的单调函数 ,可记作 k(||x-x~c~||)，其作用往往是局部的 , 即当x远离x~c~时函数取值很小。最常用的径向基函数是高斯核函数，形式为

（3）几种特殊的映射函数

①（最常用）高斯径向基函数（Gauss函数）

其中，r为到中心的距离，σ为函数的宽度参数，控制了函数的径向作用范围。如果距离为0那么核函数值为1，距离越远衰减越快，其中高斯径向基的参数σ在支持向量机中被称为到达率或者说函数跌落到零的速度。由于这个函数类似于高斯分布，因此称为高斯核函数。

②反演S型函数（Reflected Sigmoidal函数）

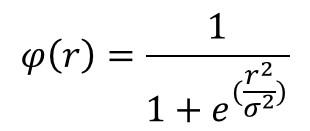
③拟多二次函数（Inverse multiquadrics函数）

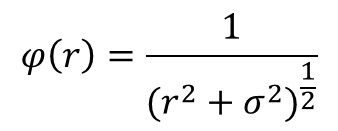
2.正则化RBF神经网络

（1）网络结构

网络具有N个输入节点(i)，P个隐节点(j)，L个输出节点(k)；网络隐节点数等于样本数P，隐节点的激活函数通常是高斯径向基函数，并将所有样本数设为径向基函数的中心（第p个样本设为第p个隐节点的径向基函数的中心），各径向基函数取统一的扩展常数。 输出层神经元采用线性激活函数。

当输入为训练集中的某个样本X^P^时，对应的期望输出d^P^就是知道信号。为了确定隐藏层到输出层之间的权值，需要将训练集中的样本逐一输入，从而得到方程组ΦW=d，求解权值矩阵。

正则化RBF网络具有以下3个特点：

① 正则化网络是一种通用逼近器，只有要足够的节点，它可以以任意精度逼近紧集上的任意多元连续函数。

② 具有最佳逼近特性，即任给一个未知的非线性函数F，总可以找到一组权值使得正则化网络对于F的逼近优于所有其可                 能的选择。

③ 正则化网络得到的解是最佳的，所谓“最佳”体现在同时满足对样本的逼近误差和逼近曲线的平滑性。

（2）算法设计【扩展常数和输出节点的权值】

径向基函数的扩展常数可根据数据中心的散布而确定，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为（其中d~max~是样本之间最大距离）：

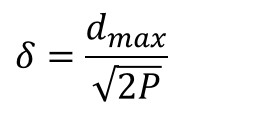
输出层的权值采用最小均方误差算法LMS，ΔW~k~的各分量为 ：

权值初始化任意值。

3.广义RBF神经网络

（1）网络结构

当样本数P很大时，可减少隐节点的个数（设为M），即N<M<<P，N为样本维数。隐节点的激活函数一般选用格林函数；输出阈值向量T=(T~1~,T~2~,...,T~L~)

广义RBF网络具有以下4个特点：

①  径向基函数的个数M与样本的个数P不相等，且M常常远小于P。
②  径向基函数的中心不再限制在数据点上，而是由训练算法确定。
③  各径向基数的扩展常数不再统一，其值由训练算法确定。
④  输出函数的线性中包含阈值参数，用于补偿基函数在样本集上的平均值与目标值之间的差别。

（2）方法设计【各基函数的数据中心，扩展常数以及输出节点的权值】

  • 数据中心从样本输人中选取。一般来说，样本密集的地方中心点可以适当多些，样本稀疏的地方中心点可以少些；若数据本身是均匀分布的，中心点也可以均匀分布。总之，选出的数据中心应具有代表性。径向基函数的扩展常数是根据数据中心的散布而确定的，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为（其中d~max~是样本之间最大距离；M是数据中心的数目）：

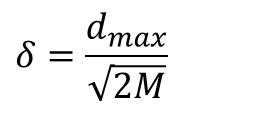
  • 常采用各种动态聚类算法对数据中心进行自组织选择，在学习过程中需对数据中心的位置进行动态调节。常用的方法是K-means聚类，其优点是能根据各聚类中心之间的距离确定各隐节点的扩展常数。由于RBF网的隐节点数对其泛化能力有极大的影响，所以寻找能确定聚类数目的合理方法，是聚类方法设计RBE网时需首先解决的问题。除聚类算法外，还有梯度训练方法、资源分配网络（RAN)等。

【例】广义RBF网络数据中心的聚类算法

第一阶段常采用K-means聚类算法，其任务是用自组织聚类方法为隐层节点的径向基函数确定合适的数据中心，并根据各中心之间的距离确定隐节点的扩展常数。在聚类确定数据中心的位置之前，需要先估计中心的个数M（从而确定了隐节点数），一般需要通过试验来决定。扩展常数的确定是通过k个聚类中心点的距离决定的，一般是k个中心点彼此距离最小的那个值d的λ倍 。

（K-means聚类算法原理：在数据中随意选择k个中心点，然后以这k个中心数据为基础计算其他数据到此中心的距离，并把新数据加入最近的那个中心点，每加入一个数据就计算平均距离然后以这个平均距离作为本类的新中心，直到数据分类完成了。）

第二阶段为监督学习阶段，其任务是用有监督学习算法训练输出层权值，一般采用LMS法/梯度法进行训练。更简捷的方法是用伪逆法直接计算。

 

 

 

 

 

 

 

 

 

整理自：

1.神经网络七十年:回顾与展望  2016 焦李成

http://kns-cnki-net-s.ivpn.hit.edu.cn:1080/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2016&filename=JSJX201608015&uid=WEEvREcwSlJHSldRa1FhdXNzY2Z2V3hhM2M2bUtsQWJXVE11OXUrcFhKOD0=$9A4hF_YAuvQ5obgVAqNKPCYcEjKensW4IQMovwHtwkF4VYPoHbKxJw!!&v=MDQyMzExVDNxVHJXTTFGckNVUjdxZllPUnRGeXJuVkwvSkx6N0Jkckc0SDlmTXA0OUVZWVI4ZVgxTHV4WVM3RGg=

2.https://www.cnblogs.com/subconscious/p/5058741.html#tenth

3.https://blog.csdn.net/weixin_42398658/article/details/83991773

4.https://blog.csdn.net/richard2357/article/details/23184999?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.channel_param

5.https://www.cnblogs.com/pythonlearing/p/9978246.html

6.https://www.cnblogs.com/shona/p/10944477.html

7.https://www.cnblogs.com/how-chang/p/9638684.html

8.https://www.jiqizhixin.com/graph/technologies/672e5579-ffb9-4006-b5f8-7a9233f9c527

9.http://c.biancheng.net/view/1954.html

10.https://blog.csdn.net/itplus/article/details/19168967

11.https://blog.csdn.net/itplus/article/details/19408143

12.https://blog.csdn.net/itplus/article/details/19408701

13.https://www.jiqizhixin.com/graph/technologies/112ef6e6-4701-4b8d-bbc4-f8a1893ec0b5

14.https://www.bilibili.com/video/av16577449/?spm_id_from=333.788.videocard.0

15.https://blog.csdn.net/zwqjoy/article/details/82254602

16.https://blog.csdn.net/weixin_38740463/article/details/87968788?utm_medium=distribute.pc_relevant.none-task-blog-baidulandingword-5&spm=1001.2101.3001.4242

17.https://m.imooc.com/article/269657

18.https://blog.csdn.net/bitcarmanlee/article/details/51154481

19.https://blog.csdn.net/bitcarmanlee/article/details/51165444

20.https://blog.csdn.net/u014313009/article/details/51039334

21.https://blog.csdn.net/weixin_36670529/article/details/100101609

22.https://blog.csdn.net/qq_30232405/article/details/54142494

23.https://www.jianshu.com/p/01e5b1b5cb32

24.https://blog.csdn.net/leonardohaig/article/details/89416516

25.https://blog.csdn.net/weixin_42398658/article/details/83215916

26.https://blog.csdn.net/huang1024rui/article/details/51510611

27.https://blog.csdn.net/weixin_42398658/article/details/84342747

 

这篇关于【笔记】神经网络——Rita_Aloha的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/160949。

相关文章

图神经网络模型介绍（1）

图神经网络模型介绍（1）

我们将图神经网络分为基于谱域的模型和基于空域的模型，并按照发展顺序详解每个类别中的重要模型。 1.1基于谱域的图神经网络         谱域上的图卷积在图学习迈向深度学习的发展历程中起到了关键的作用。本节主要介绍三个具有代表性的谱域图神经网络：谱图卷积网络、切比雪夫网络和图卷积网络。 （1）谱图卷积网络 卷积定理：函数卷积的傅里叶变换是函数傅里叶变换的乘积，即F{f*g}
阅读更多...
【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系列文章目录 监督学习：参数方法 【学习笔记】 陈强-机器学习-Python-Ch4 线性回归 【学习笔记】 陈强-机器学习-Python-Ch5 逻辑回归 【课后题练习】 陈强-机器学习-Python-Ch5 逻辑回归（SAheart.csv） 【学习笔记】 陈强-机器学习-Python-Ch6 多项逻辑回归 【学习笔记 及 课后题练习】 陈强-机器学习-Python-Ch7 判别分析 【学
阅读更多...
系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

本章知识考点：         第20课时主要学习通信系统架构设计的理论和工作中的实践。根据新版考试大纲,本课时知识点会涉及案例分析题(25分),而在历年考试中,案例题对该部分内容的考查并不多,虽在综合知识选择题目中经常考查,但分值也不高。本课时内容侧重于对知识点的记忆和理解,按照以往的出题规律,通信系统架构设计基础知识点多来源于教材内的基础网络设备、网络架构和教材外最新时事热点技术。本课时知识
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划 非线性规划1. 模型原理1.1 非线性规划的标准型1.2 非线性规划求解的Matlab函数 2. 典型例题3. matlab代码求解3.1 例1 一个简单示例3.2 例2 选址问题1. 第一问 线性规划2. 第二问 非线性规划 非线性规划 非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。2
阅读更多...
【C++学习笔记 20】C++中的智能指针

【C++学习笔记 20】C++中的智能指针

智能指针的功能 在上一篇笔记提到了在栈和堆上创建变量的区别，使用new关键字创建变量时，需要搭配delete关键字销毁变量。而智能指针的作用就是调用new分配内存时，不必自己去调用delete，甚至不用调用new。 智能指针实际上就是对原始指针的包装。 unique_ptr 最简单的智能指针，是一种作用域指针，意思是当指针超出该作用域时，会自动调用delete。它名为unique的原因是这个
阅读更多...
查看提交历史 —— Git 学习笔记 11

查看提交历史 —— Git 学习笔记 11

查看提交历史 查看提交历史 不带任何选项的git log-p选项--stat 选项--pretty=oneline选项--pretty=format选项git log常用选项列表参考资料 在提交了若干更新，又或者克隆了某个项目之后，你也许想回顾下提交历史。 完成这个任务最简单而又有效的 工具是 git log 命令。 接下来的例子会用一个用于演示的 simplegit
阅读更多...
记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 文章目录 文件的状态三个区域检查当前文件状态跟踪新文件取消跟踪（un-tracking）文件重新跟踪（re-tracking）文件暂存已修改文件忽略某些文件查看已暂存和未暂存的修改提交更新跳过暂存区删除文件移动文件参考资料 咱们接着很多天以前的 取得Git仓库 这篇文章继续说。 文件的状态 不管是通过哪种方法，现在我们已经有了一个仓库，并从这个仓
阅读更多...
忽略某些文件 —— Git 学习笔记 05

忽略某些文件 —— Git 学习笔记 05

忽略某些文件 忽略某些文件 通过.gitignore文件其他规则源如何选择规则源参考资料 对于某些文件，我们不希望把它们纳入 Git 的管理，也不希望它们总出现在未跟踪文件列表。通常它们都是些自动生成的文件，比如日志文件、编译过程中创建的临时文件等。 通过.gitignore文件 假设我们要忽略 lib.a 文件，那我们可以在 lib.a 所在目录下创建一个名为 .gi
阅读更多...
取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04 我认为， Git 的学习分为两大块：一是工作区、索引、本地版本库之间的交互；二是本地版本库和远程版本库之间的交互。第一块是基础，第二块是难点。 下面，我们就围绕着第一部分内容来学习，先不考虑远程仓库，只考虑本地仓库。 怎样取得项目的 Git 仓库？ 有两种取得 Git 项目仓库的方法。第一种是在本地创建一个新的仓库，第二种是把其他地方的某个
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2