HDLBits——Arithmetic Circuits

HDLBits——Arithmetic Circuits

Problem 65 : Half adder (Hadd)

Requirement：

本题中需要实现一个 2 进制 1bit 加法器，加法器将输入的两个 1bit 数相加，产生两数相加之和以及进位。

Solution：

module top_module( input a, b,output cout, sum );assign {cout,sum} = a + b;endmodule

Problem 66 : Full adder (Fadd)

Requirement：

本题中需要实现一个 2 进制 1bit 全加器，全加器与上一题中的加法器的区别在于需要累加来自前级的进位。

Solution：

module top_module( input a, b, cin,output cout, sum );assign {cout,sum} = a + b + cin;endmodule

Timing Diagram：

Problem 67 : 3-bit binary adder(Adder3 )

Requirement：

本题中需要通过实例化 3 个全加器，并将它们级联起来实现一个位宽为 3 bit 的二进制加法器。其实 3 bit 的加法器 cout 也只需要一位就够了，直接 assign {cout,sum} = a + b + cin。这里给了三位是暗示包括了每一位上的进位，即需要例化 3 个全加器模块，而不是一条 assign 语句。

Solution：

module top_module( input [2:0] a, b,input cin,output [2:0] cout,output [2:0] sum );add1 add1(a[0],b[0],cin,cout[0],sum[0]);  add1 add2(a[1],b[1],cout[0],cout[1],sum[1]);add1 add3(a[2],b[2],cout[1],cout[2],sum[2]);  endmodulemodule add1( input a, b, cin,output cout, sum );assign {cout,sum} = a + b + cin;endmodule

//also
assign sum = a ^ b ^ cin;
assign cout = a&b | a&cin | b&cin;

Timing Diagram：

Problem 68 : Adder (Exams/m2014 q4j)

Requirement：

实现下图中的电路，一个 4-bit 全加器，FA：full adder 全加器。

Solution：

module top_module (input [3:0] x,input [3:0] y, output [4:0] sum);assign sum = x + y;endmodule

verilog 的语法会自动将 x+y 扩展成 5 bit 数，但如果使用位连接符 {x+y}，那么结果就会被限制为 4 bit 数。

Problem 69 : Signed addition overflow (Exams/ece241 2014 q1c)

Requirement：

有符号数相加的溢出问题，实现一个 2 进制 8bit 有符号数加法器，加法器将输入的两个 8bit 数补码相加，产生相加之和以及进位。

Solution：

方法一：判断变号与否。

有符号数溢出有两种情况：一是正正相加，产生负数；另一种情况是负负相加，产生正数。

module top_module (input [7:0] a,input [7:0] b,output [7:0] s,output overflow
); //assign s = a + b;assign overflow = (a[7]&b[7]&~s[7])|(~a[7]&~b[7]&s[7]);endmodule

方法二：判断数值位和符号位是否同时进位（双符号位）。

module top_module (input [7:0] a,input [7:0] b,output [7:0] s,output overflow
); wire [8:0] t;assign t = {a[7],a} + {b[7],b};assign s = t;assign overflow = t[8]^t[7];endmodule

Timing Diagram：

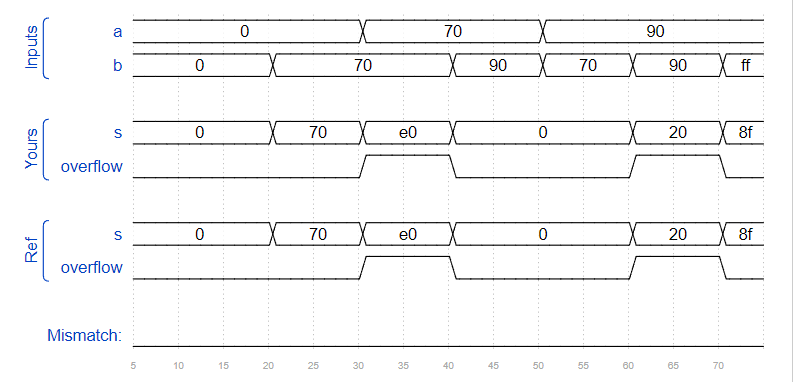
Problem 70 100-bit binary adder

Requirement：

题目要求我们创建一个 100bit 的二进制的加法器，该电路共包含两个 100bit 的输入和一个 cin， 输出产生 sum 和 cout。

Solution：

module top_module( input [99:0] a, b,input cin,output cout,output [99:0] sum );assign {cout,sum} = cin + a + b;endmodule

虽然这样就足够简单了，但还是练习一下 for 循环吧。

always-for：

module top_module( input [99:0] a, b,input cin,output reg cout,output reg [99:0] sum );reg [99:0] cout100;integer i;always @(*) begin{cout100[0],sum[0]} = a[0] + b[0] + cin;for(i=1;i<100;i=i+1)begin{cout100[i],sum[i]} = a[i] + b[i] + cout100[i-1];endcout = cout100[99];endendmodule

generate-for：

module top_module( input [99:0] a, b,input cin,output cout,output [99:0] sum );wire [99:0] cout100;assign {cout100[0],sum[0]} = a[0] + b[0] + cin;genvar i;generatefor(i=1;i<100;i=i+1)begin:add100assign {cout100[i],sum[i]} = a[i] + b[i] + cout100[i-1];endendgenerateassign cout = cout100[99];endmodule

PS：例化时 begin 块要有标签名的原因：generate 循环中例化的模块名为add100[1].例化名，add100[2].例化名.……add100[99].例化名，这样就算例化名里没有 i，也不怕重复。

Problem 71 4-digit BCD adder

Requirement：

在本题中，题目给我们提供了一个 BCD 加法器名字为 bcd_fadd， 输入为两个 4bitBCD 码，一个 cin，产生输出为 sum 和 cout。

已知：

module bcd_fadd {input [3:0] a,input [3:0] b,input     cin,output   cout,output [3:0] sum );

Solution：

module top_module( input [15:0] a, b,input cin,output cout,output [15:0] sum );wire [4:0] cout16;assign cout16[0] = cin;genvar i;generatefor(i=0;i<4;i=i+1)begin:add16bcd_fadd bcd_fadd_i(a[4*i+:4],b[4*i+:4],cout16[i],cout16[i+1],sum[4*i+:4]);endendgenerateassign cout = cout16[4];endmodule

错过：不管多少位宽的加法，进位永远只有一位。

唯一的感受：困