本文主要是介绍HDLBits练习 Circuits;Combinational Logic;Arithmetic Circuits,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Circuits;Arithmetic Circuits
- 1.Half adder
- 2.Full adder
- 3.3-bit binary adder
- 4.Adder
- 5.Signed addition overflow
- 6.100-bit binary adder
- 7.4-digit BCD adder
- 7. ==问题==
要点:
1. 异或的理解:
异或(相异的时候进行或运算)真值表为
| A | B | P |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
运算符为 " ^ "
2. 全加器与半加器的区别
半加器:两个数产生进位但不能够处理来自上一级的进位。真值表为:
| a | b | cout | sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
全加器:除了两个数的输入,输入还包括上一级的进位值。自然输出也会有一个进位值。真值表为:
| a | b | cout-in(上一级进位) | cout-out(进位) | sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
可以由两个半加器拼接成一个全加器

1.Half adder
例1:

解:
要求实现半加器
module top_module( input a, b,output cout, sum );assign sum = a ^ b;assign cout = a & b;
endmodule
或者直接实现
module top_module( input a, b,output cout, sum );assign {cout,sum} = a + b;
endmoudle
2.Full adder
例1:

实现1bit 全加器
解:
直接想到的方法就是真值表得到逻辑式
| a | b | cout-in(上一级进位) | cout-out(进位) | sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |


module top_module( input a, b, cin,output cout, sum );assign cout = (a & cin)|(a & b)|(b & cin);assign sum = (~a & ~b & cin)|(~a & b& ~cin)|(a & ~b & ~cin)|(a & b & cin);
endmodule
更简单的方法 是使用位拼接符号
module top_module( input a, b, cin,output cout, sum );assign {cout , sum} = a + b + cin;
endmodule
3.3-bit binary adder
例1:

解:
要求实现一个3-bit全加器
有三种解决的方法
- 反复使用的真值表转为逻辑表达式
- 采用位拼接符号{ }进行对位的操作
- 例化1-bit全加器,使用三个1-bit全加器实现目标
这里贴上模块操作Modules:Hierarchy
//方法3
module top_module( input [2:0] a, b,input cin,output [2:0] cout,output [2:0] sum
);adder u1 (.a(a[0]),.b(b[0]),.cin(cin),.cout(cout[0]),.sum(sum[0])
);adder u2 (.a(a[1]),.b(b[1]),.cin(cout[0]),.cout(cout[1]),.sum(sum[1])
);adder u3 (.a(a[2]),.b(b[2]),.cin(cout[1]),.cout(cout[2]),.sum(sum[2])
);
endmodule
module adder(//由于没有例化好的adder模块需要自己补上input a,b,cin,output cout,sum
);assign {cout,sum} = a + b + cin;
endmodule
4.Adder
例1:
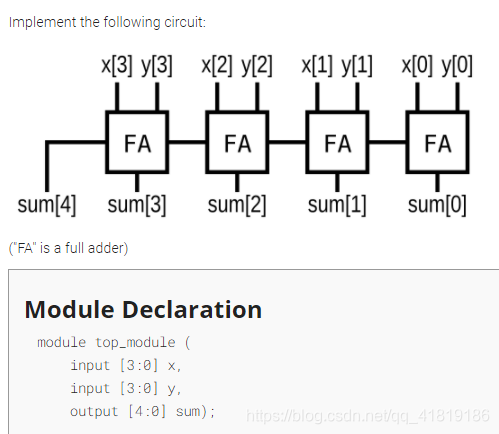
实现图中的4-bit加法器
解:
由于有四个全加器想到了上题使用的例化的方法
module top_module (input [3:0] x,input [3:0] y, output [4:0] sum);wire cout[2:0];adder u1 (.a(x[0]),.b(y[0]),.cin(1'b0),.cout(cout[0]),.sum(sum[0]),);adder u2 (.a(x[1]),.b(y[1]),.cin(cout[0]),.cout(cout[1]),.sum(sum[1]),);adder u3 (.a(x[2]),.b(y[2]),.cin(cout[1]),.cout(cout[2]),.sum(sum[2]),);adder u4 (.a(x[3]),.b(y[3]),.cin(cout[2]),.cout(sum[4]),.sum(sum[3]),);
endmodule
module adder (//给出全加器模块input a,b,cin,output cout,sum
);assign {cout,sum} = a + b + cin;
endmodule
看了知乎上的解答,可以直接使用assign sum = x + y 如果产生进位会直接扩展成为五位二进制数 (- _ -)
module top_module (input [3:0] x,input [3:0] y, output [4:0] sum);assign sum = x + y;
endmodule
5.Signed addition overflow
例1:

解:
本题希望实现signed integer(有符号数)的加减并判断溢出,较难理解的是有关overflow的判断,关于有符号数的规则参考真 OO无双
module top_module (input [7:0] a,input [7:0] b,output [7:0] s,output overflow
); wire[8:0]t;assign t = {a[7],a} + {b[7],b} ;assign s = t[7:0];assign overflow = t[8] ^ t[7];endmodule
本题任然存在较多疑问
6.100-bit binary adder
例1:

实现100bit全加器
解:
直接采用位拼接运算
module top_module( input [99:0] a, b,input cin,output cout,output [99:0] sum );assign {cout,sum} = a + b + cin;
endmodule
7.4-digit BCD adder
例1:
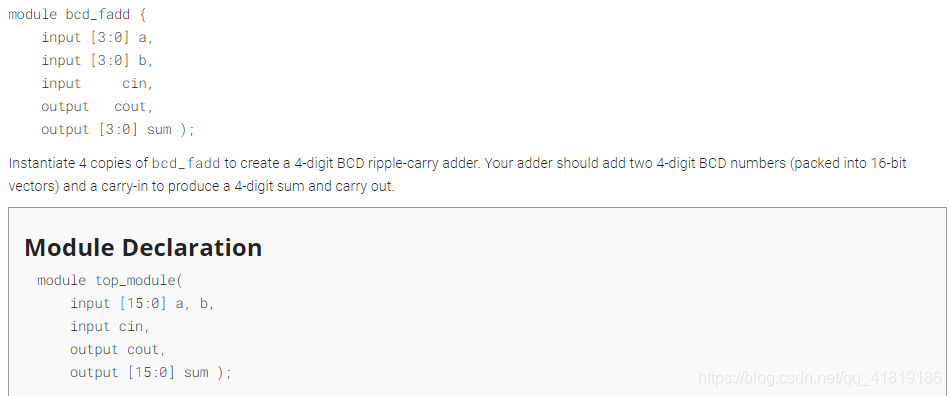
题目中已经提供了BCD加法器bcd_fadd,需要实现一个16-bit的BCD加法器
解:
只需要简单例化4次就可以解决问题
module top_module( input [15:0] a, b,input cin,output cout,output [15:0] sum );wire [3:0] cout_temp;bcd_fadd u1(.a(a[3:0]),.b(b[3:0]),.cin(cin),.cout(cout_temp[0]),.sum(sum[3:0]));bcd_fadd u2(.a(a[7:4]),.b(b[7:4]),.cin(cout_temp[0]),.cout(cout_temp[1]),.sum(sum[7:4]));bcd_fadd u3(.a(a[11:8]),.b(b[11:8]),.cin(cout_temp[1]),.cout(cout_temp[2]),.sum(sum[11:8]));bcd_fadd u4(.a(a[15:12]),.b(b[15:12]),.cin(cout_temp[2]),.cout(cout_temp[3]),.sum(sum[15:12]));assign cout = cout_temp[3];endmodule
7. 问题
5
这篇关于HDLBits练习 Circuits;Combinational Logic;Arithmetic Circuits的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




