罗德里格斯公式的推导过程

最近在学高翔博士的《视觉SLAM十四讲》，看到第三章中的课后题中要求理解罗德里格斯公式的推导过程，所以在CSDN上搜了一篇文章，原文链接http://blog.csdn.net/q583956932/article/details/78933245

原文写的十分精湛，大家可以直接看原文就好了，

以下是我在看这篇文章时所需要巩固的知识点（现在是大三狗，早把大一的知识点忘了。。。）

点积（来自维基百科）：

        是两个向量上的函數并返回一个标量的二元运算，它的结果是欧几里得空间的标准内积。兩個向量的点积寫作a·b，数量积及标量积。

代数定义：

两个向量 a → {\displaystyle {\vec {a}}} = [a₁, a₂,…, a_n]和 b → {\displaystyle {\vec {b}}} = [b₁, b₂,…, b_n]的点积定义为：

a → ⋅ b → = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle {\vec {a}}\cdot {\vec {b}}=\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

这裡的Σ是求和符号，而n是向量空間的維數。

例如，两个三维向量[1, 3, -5]和[4, -2, -1]的点积是

  [ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 ) ( 4 ) + ( 3 ) ( − 2 ) + ( − 5 ) ( − 1 ) = 4 − 6 + 5 = 3 {\displaystyle {\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1)(4)+(3)(-2)+(-5)(-1)\\&=4-6+5\\&=3\end{aligned}}}

点积还可以写为：

a → ⋅ b → = | a → b → T | {\displaystyle {\vec {a}}\cdot {\vec {b}}=|{\vec {a}}{\vec {b}}^{T}|} 。

这裡， b → T {\displaystyle {\vec {b}}^{T}} 是行向量 b → {\displaystyle {\vec {b}}} 的转置，而 | a → b → T | {\displaystyle |{\vec {a}}{\vec {b}}^{T}|} 是 a → b → T {\displaystyle {\vec {a}}{\vec {b}}^{T}} 的行列式。使用上面的例子，一个1×3矩阵（行向量）乘以一个3×1矩阵（列向量）的行列式就是结果(通过矩阵乘法得到1×1矩阵，再利用行列式得出純量答案):

| [ 1 3 − 5 ] [ 4 − 2 − 1 ] T | = | 3 | = 3 {\displaystyle |{\begin{bmatrix}1&3&-5\end{bmatrix}}{\begin{bmatrix}4&-2&-1\end{bmatrix}}^{T}|=|3|=3} 。

几何定义：

在欧几里得空间中，点积可以直观地定义为

a → ⋅ b → = | a → | | b → | cos ⁡ θ {\displaystyle {\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\cos \theta \;}

这里 | x → {\displaystyle {\vec {x}}} | 表示 x → {\displaystyle {\vec {x}}} 的模（长度），θ表示两个向量之间的角度。注意：点积的形式定义和这个定义不同；在形式定义中， a → {\displaystyle {\vec {a}}} 和 b → {\displaystyle {\vec {b}}} 的夹角是通过上述等式定义的。这样，两个互相垂直的向量的点积总是零。若 a → {\displaystyle {\vec {a}}} 和 b → {\displaystyle {\vec {b}}} 都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两个向量，它们之间的夹角可以通过下列公式得到：

cos ⁡ θ = a ⋅ b | a → | | b → | {\displaystyle \cos {\theta }={\frac {\mathbf {a\cdot b} }{|{\vec {a}}|\,|{\vec {b}}|}}}

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这裡，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

标量投影：

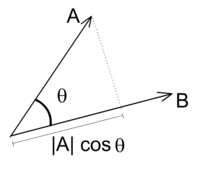A·B = |A| |B| cos(θ).|A| cos(θ)是A到B的投影。

欧氏空间中向量A在向量B上的标量投影是指

A B = | A | cos ⁡ θ {\displaystyle A_{B}=|\mathbf {A} |\cos \theta }

这里θ是A和B的夹角。从点积的几何定义 A ⋅ B = | A | | B | cos ⁡ θ {\displaystyle \mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos \theta } 不难得出，两个向量的点积： A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } 可以理解为向量 A {\displaystyle \mathbf {A} } 在向量 B {\displaystyle \mathbf {B} } 上的投影再乘以B的长度。

A ⋅ B = A B | B | = B A | A | {\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{B}|\mathbf {B} |=B_{A}|\mathbf {A} |} 外积（来自维基百科）：

   

两个向量 a {\displaystyle \mathbf {a} } 和 b {\displaystyle \mathbf {b} } 的叉积写作 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } （有时也被写成 a ∧ b {\displaystyle \mathbf {a} \wedge \mathbf {b} } ，避免和字母 x 混淆）。叉积可定义为：

a × b = | a | | b | sin ⁡ θ n ^ {\displaystyle \mathbf {a} \times \mathbf {b} =\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \theta \;{\hat {\mathbf {n} }}

在这里 θ {\displaystyle \theta } 表示 a {\displaystyle \mathbf {a} } 和 b {\displaystyle \mathbf {b} } 之间的角度（ 0 ∘ ≤ θ ≤ 180 ∘ {\displaystyle 0^{\circ }\leq \theta \leq 180^{\circ }} ），它位于这两个向量所定义的平面上。而 n ^ {\displaystyle {\hat {\mathbf {n} }}} 是一个与 a {\displaystyle \mathbf {a} } 、 b {\displaystyle \mathbf {b} } 所构成的平面垂直的单位向量。这个定义有个问题，就是同时有两个单位向量都垂直于 a {\displaystyle \mathbf {a} } 和 b {\displaystyle \mathbf {b} } ：若 n ^ {\displaystyle {\hat {\mathbf {n} }}} 满足垂直的条件，那么 − n ^ {\displaystyle -{\hat {\mathbf {n} }}} 也满足。“正确”的向量由向量空间的方向确定，即按照给定直角坐标系的左右手定则。若（ i {\displaystyle \mathbf {i} } 、 j {\displaystyle \mathbf {j} } 、 k {\displaystyle \mathbf {k} } ）满足右手定则，则（ a {\displaystyle \mathbf {a} } 、 b {\displaystyle \mathbf {b} } 、 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } ）也满足右手定则；或者两者同时满足左手定则。一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系满足右手定则，当右手的四指从 a {\displaystyle \mathbf {a} } 以不超过180°的转角转向 b {\displaystyle \mathbf {b} } 时，竖起的大拇指指向是 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } 的方向。由于向量的叉积由坐标系确定，所以其结果被称为「伪向量」。

原文开始：

   

  罗德里格斯公式（Rodriguez formula）是计算机视觉中的一大经典公式，在描述相机位姿的过程中很常用。公式：

  从旋转矩阵 R 讲起，在三维空间中，旋转矩阵 R 可以对坐标系（基向量组）进行刚性的旋转变换。

  通常为了方便计算，基向量组中的向量是相互正交的且都为单位向量，那么 R 就是一个标准正交矩阵。两个重要性质：

• RTR=R−1R=E
• |R|=1

  假设原坐标系基向量矩阵为 B ，旋转后的坐标系基向量矩阵为 C 。

  其变换过程如图所示：

  根据线性代数的定义，旋转矩阵 R 就是从基向量矩阵 B 到基向量矩阵 C 的过渡矩阵。由于旋转矩阵 R 是标准3阶正交矩阵，故旋转矩阵 R 的自由度为3，这说明最少可以用三个变量来表示旋转矩阵 R ，这就是 罗德里格斯公式（Rodriguez formula）存在的基础。

  罗德里格斯公式（Rodriguez formula）首先要确定一个三维的单位向量 k=[kxkykz]T （两个自由度）和一个标量 θ （一个自由度）。

证明方法一：

（图片摘自Wiki）

  先考虑对一个向量作旋转，其中 v 是原向量，三维的单位向量 k=[kxkykz]T 是旋转轴， θ 是旋转角度， vrot 是旋转后的向量。

  先通过点积得到 v 在 k 方向的平行分量 v∥ 。

  再通过叉乘得到与 k 正交的两个向量 v⊥ 和 w 。

  这样，我们就得到了3个相互正交的向量。不难得出：

  再引入叉积矩阵的概念：记 K 为 k=[kxkykz]T 的叉积矩阵。显然 K 是一个反对称矩阵。

  他有如下性质：

  为了利用该性质，需要将 vrot 代换为 v 与 k 的叉积关系，先根据（1）式做代换：

  然后得到：

  根据叉积矩阵性质：

  最后将 v、vrot 换为 B、C ，就是罗德里格斯公式的标准形式。

  方法一证毕。

在想理解公式一的时候，把W=kXv代入，能更方便理解一些。

就是这样，感谢原文作者分享