Multi-gate Mixture-of-Experts（MMoE）

1. 概述

在工业界经常会面对多个学习目标的场景，如在推荐系统中，除了要给用户推荐刚兴趣的物品之外，一些细化的指标，包括点击率，转化率，浏览时长等等，都会作为评判推荐系统效果好坏的重要指标，不同的是在不同的场景下对不同指标的要求不一样而已。在面对这种多任务的场景，最简单最直接的方法是针对每一个任务训练一个模型，显而易见，这种方式带来了巨大的成本开销，包括了计算成本和存储成本。多任务学习（Multi-task Learning）便由此而生，在多任务学习中，希望通过一个模型可以同时学习多个目标。然而在多任务学习中，多个任务之间通常存在着或是彼此联系或是巨大差异的现象，这就导致了多任务模型常常效果不佳。Google于2018年提出了Multi-gate Mixture-of-Experts（MMoE）模型[1]来对任务之间相互关系建模。

2. 算法原理

MMoE模型并不是凭空产出的，是在前人的工作上做了很多改进。多任务学习经过多年的发展，历史上也出现了很多多任务学习的模型。

2.1. Shared-Bottom模型

在多任务学习模型当中，最常见的一种模型就是shared-bottom模型，shared-bottom模型的结构如下图所示：

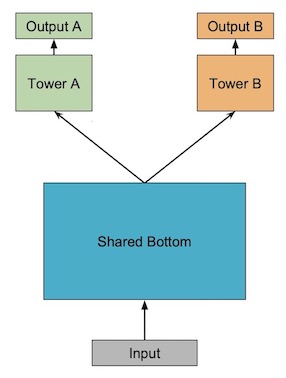
在shared-bottom模型中，每个任务都共享底部的网络，如上图中的Shared Bottom部分，然后在上层再根据任务的不同划分出多个tower network来分别学习不同的目标，如上图中的TowerA和Tower B。假设当前有$K$个任务，输入特征通过shared-bottom网络后可以由函数$f$表示，每一个tower网络的输出为函数$h^k$，其中$k=1,2,\cdots ,K$，则shared-bottom模型可以表示为：

$$y_k=h^k\left(f\left(x\right)\right)$$

2.2. Multi-gate Mixture-of-Experts（MMoE）模型

从MMoE的名称来看，可以看到主要包括两个部分，分别为：Multi-gate（多门控网络）和Mixture-of-Experts（混合专家）。

2.2.1. Mixture-of-Experts（MoE）模型

MoE模型可以表示为

$$y=\sum _{i=1}^{n}g{\left(x\right)}_i{f}_i\left(x\right)$$

其中${\sum }_{i=1}^{n}g{\left(x\right)}_i=1$，$g{\left(x\right)}_i$表示的是$g\left(x\right)$的第$i$个输出值，代表的是选择专家$f_i$的概率值。$f_i\left(x\right)$是第$i$个专家网络的值。MoE可以看作是基于多个独立模型的集成方法Ensemble，通过Ensemble的知识可知，通过Ensemble能够提高模型的性能。

也有将MoE作为一个独立的层[2]，将多个MoE结构堆叠在另一个网络中，一个MoE层的输出作为下一层MoE层的输入，其输出作为另一个下一层的输入，其具体过程如下图所示：

2.2.2. One-gate Mixture-of-Experts（OMoE）模型

在shared-bottom模型中，无法实现对多个任务之间关系的建模，结合shared-bottom和MoE，便有了One-gate Mixture-of-Experts模型，其具体过程如下图所示：

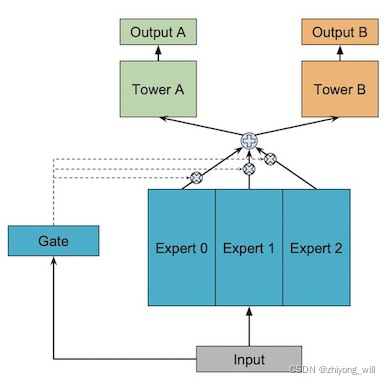
假设当前有$K$个任务，与Shared-Bottom模型一样，输入特征通过多个专家网络后可以由函数$f_i\left(x\right)$表示，假设当前有$n$个专家网络，即$i=1,2,\cdots ,n$，每一个任务对应的tower网络的输出为函数$h^k$，其中$k=1,2,\cdots ,K$，则OMoE模型可以表示为：

$$y_k=h^k\left(\sum _{i=1}^{n}g{\left(x\right)}_i{f}_i\left(x\right)\right)$$

2.2.3. Multi-gate Mixture-of-Experts（MMoE）模型

Multi-gate Mixture-of-Experts是One-gate Mixture-of-Experts的升级版本，借鉴门控网络的思想，将OMoE模型中的One-gate升级为Multi-gate，针对不同的任务有自己独立的门控网络，每个任务的gating networks通过最终输出权重不同实现对专家的选择。不同任务的门控网络可以学习到对专家的不同组合，因此模型能够考虑到了任务之间的相关性和区别。其具体过程如下图所示：

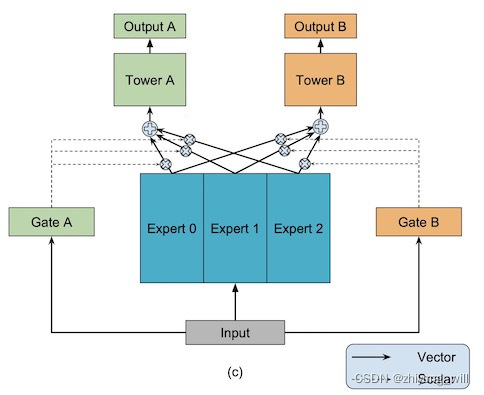
同样，假设当前有$K$个任务，输入特征通过多个专家网络后可以由函数$f_i\left(x\right)$表示，假设当前有$n$个专家网络，即$i=1,2,\cdots ,n$，每一个任务对应的tower网络的输出为函数$h^k$，其中$k=1,2,\cdots ,K$，则MMoE模型可以表示为：

$$y_k=h^k\left(\sum _{i=1}^n{g}^k{\left(x\right)}_i{f}_i\left(x\right)\right)$$

其中，$g^k{\left(x\right)}_i$为门控网络，可以由一个最简单的网络表示：

$$g^k\left(x\right)=softmax\left(W_{gk}x\right)$$

其中，$W_{gk}\in {\mathbb{R}}^{n\times d}$，$n$表示专家的个数，$d$表示的是特征的维度。

3.总结

通过结合门控网络和混合专家组成的MMoE模型，从实验的结论上来看，能够利用同一个模型对多个任务同时建模，同时能够对多个任务之间的联系和区别建模。

参考文献

[1] Ma J, Zhao Z, Yi X, et al. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 1930-1939.

[2] Shazeer, Noam, et al. “Outrageously large neural networks: The sparsely-gated mixture-of-experts layer.” arXiv preprint arXiv:1701.06538 (2017).