本文主要是介绍kmeans,学习向量量化lvq,高斯聚类函数GaussianMixture的python实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、介绍
- 1、概念介绍
- (1)数据集
- (2)实验内容
- (3)kmeans算法
- (4)学习向量量化lvq算法
- (5)高斯聚类函数算法
- (6)acc精度计算
- (7)标准互信息计算
- 2、函数介绍
- 二、模型函数
- (1)导包
- (2)手写kmeans函数
- (3)手写学习向量量化lvq函数
- (4)手写高斯聚类函数
- (5)标准互信息计算
- (6)匈牙利算法做标签映射
- (7)精度计算
- 三、手写函数进行聚类
- 四、sklearn官方函数
- 五、结果:
- (1)acc结果对比
- (2)nmi结果对比
- (3)结果分析
- (4)控制台输出
一、介绍
1、概念介绍
(1)数据集
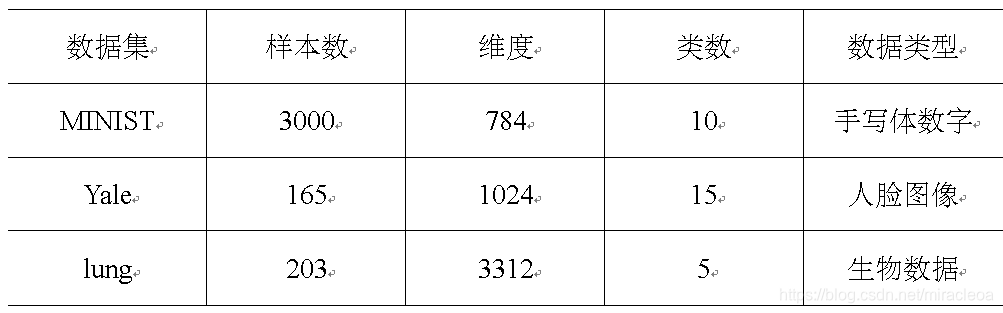
(2)实验内容

(3)kmeans算法

(4)学习向量量化lvq算法

(5)高斯聚类函数算法

(6)acc精度计算

(7)标准互信息计算


2、函数介绍
-
official_classification.py : 使用了较多的sklearn中提供的聚类函数
-
self_classification.py : 使用了手写聚类函数聚类(手写高斯聚类由于计算高维矩阵n次方报 错,就没有使用)
-
两者可以相互比较看手写函数效果如何。
-
model.py : 其中包含了kmeans,lvq,mixture-of-gaussian聚类函数,以及计算精度和NMI的手写函数,处理标签映射的匈牙利算法函数processing_label(手撸)。
-
由于学习向量量化是依据ground truth的得到的一组原型向量,是有监督的学习,因此计算其精度没有意义,在函数里就没有计算精度和NMI,只打印出了原型向量
-
函数运行时会有warning,不用在意,手写的函数没有优化,速度较慢
-
代码对三个数据集,分别使用了kmeans,lvq,mixture-of-gaussian三个方法,在得到预测标签后,采用匈牙利算法对标签进行处理,计算其精确度acc和标准互信息nmi
-
运行方法:
安装相应需求的库,直接运行official_classification.py或 self_classification.py即可
二、模型函数
(1)导包
import copy
from collections import Counterimport math
import numpy as np
from scipy.optimize import linear_sum_assignment
(2)手写kmeans函数
# KMeans函数
class KMeans:def __init__(self, n_clusters, max_iter=2000):self.n_clusters = n_clustersself.max_iter = max_iterdef dist(self, x1, x2):return np.linalg.norm(x1 - x2)def get_label(self, x):min_dist_with_mu = 999999label = -1for i in range(self.mus_array.shape[0]):dist_with_mu = self.dist(self.mus_array[i], x)if min_dist_with_mu > dist_with_mu:min_dist_with_mu = dist_with_mulabel = ireturn labeldef get_mu(self, X):index = np.random.choice(X.shape[0], 1, replace=False)mus = list()mus.append(X[index])for _ in range(self.n_clusters - 1):max_dist_index = 0max_distance = 0for j in range(X.shape[0]):min_dist_with_mu = 999999for mu in mus:dist_with_mu = self.dist(mu, X[j])if min_dist_with_mu > dist_with_mu:min_dist_with_mu = dist_with_muif max_distance < min_dist_with_mu:max_distance = min_dist_with_mumax_dist_index = jmus.append(X[max_dist_index])# print(mus)mus_array = np.array([])# print(mus[0].shape)for i in range(self.n_clusters):if i == 0:# (1,2)mus_array = mus[i]else:# (,2)-->(1,2)mus[i] = mus[i].reshape(mus[0].shape)mus_array = np.append(mus_array, mus[i], axis=0)# print(mus_array)return mus_arraydef init_mus(self):for i in range(self.mus_array.shape[0]):self.mus_array[i] = np.array([0] * self.mus_array.shape[1])def fit(self, X):self.mus_array = self.get_mu(X)iter = 0while (iter < self.max_iter):old_mus_array = copy.deepcopy(self.mus_array)Y = []# 将X归类for i in range(X.shape[0]):y = self.get_label(X[i])Y.append(y)self.init_mus()# 将同类的X累加for i in range(len(Y)):self.mus_array[Y[i]] += X[i]count = Counter(Y)# 计算出Y中各个标签的个数# 计算新的mufor i in range(self.n_clusters):self.mus_array[i] = self.mus_array[i] / count[i]diff = 0for i in range(self.mus_array.shape[0]):diff += np.linalg.norm(self.mus_array[i] - old_mus_array[i])if diff == 0:breakiter += 1self.E = 0for i in range(X.shape[0]):self.E += self.dist(X[i], self.mus_array[Y[i]])print('E = {}'.format(self.E))return np.array(Y)
(3)手写学习向量量化lvq函数
# 学习向量量化函数
class LVQ:def __init__(self, max_iter=2000, eta=0.1, e=0.01):self.max_iter = max_iterself.eta = etaself.e = edef dist(self, x1, x2):return np.linalg.norm(x1 - x2)def get_mu(self, X, Y):k = len(set(Y))index = np.random.choice(X.shape[0], 1, replace=False)mus = []mus.append(X[index])mus_label = []mus_label.append(Y[index])for _ in range(k - 1):max_dist_index = 0max_distance = 0for j in range(X.shape[0]):min_dist_with_mu = 999999# 找与mu最近的那个距离for mu in mus:dist_with_mu = self.dist(mu, X[j])if min_dist_with_mu > dist_with_mu:min_dist_with_mu = dist_with_mu# 先找各点到锚点的最短距离,即找出各点到其聚类中心的距离,# 然后再找出距离聚类中心最远的点,将其加入到聚类中心集合中if max_distance < min_dist_with_mu:max_distance = min_dist_with_mumax_dist_index = jmus.append(X[max_dist_index])mus_label.append(Y[max_dist_index])# 获取三个聚簇中心点,以及其标签mus_array = np.array([])for i in range(k):if i == 0:mus_array = mus[i]else:mus[i] = mus[i].reshape(mus[0].shape)mus_array = np.append(mus_array, mus[i], axis=0)mus_label_array = np.array(mus_label)return mus_array, mus_label_arraydef get_mu_index(self, x):min_dist_with_mu = 999999index = -1for i in range(self.mus_array.shape[0]):dist_with_mu = self.dist(self.mus_array[i], x)if min_dist_with_mu > dist_with_mu:min_dist_with_mu = dist_with_muindex = ireturn indexdef fit(self, X, Y):self.mus_array, self.mus_label_array = self.get_mu(X, Y)iter = 0while (iter < self.max_iter):# 三个聚簇中心点old_mus_array = copy.deepcopy(self.mus_array)index = np.random.choice(Y.shape[0], 1, replace=False)# 计算出每一个X距离最近的聚簇中心点,并把设其为该点中心mu_index = self.get_mu_index(X[index])if self.mus_label_array[mu_index] == Y[index]:# 0.9(p-x)^2self.mus_array[mu_index] = self.mus_array[mu_index] + \self.eta * (X[index] - self.mus_array[mu_index])else:# 1.1(p-x)^2self.mus_array[mu_index] = self.mus_array[mu_index] - \self.eta * (X[index] - self.mus_array[mu_index])diff = 0for i in range(self.mus_array.shape[0]):diff += np.linalg.norm(self.mus_array[i] - old_mus_array[i])if diff < self.e:print('迭代{}次退出'.format(iter))returniter += 1print("迭代超过{}次,退出迭代".format(self.max_iter))
(4)手写高斯聚类函数
class GaussianMixture:def __init__(self, n_clusters, max_iter=30, e=0.0001):self.n_clusters = n_clustersself.max_iter = max_iterself.e = eself.ll = 0def dist(self, x1, x2):return np.linalg.norm(x1 - x2)def get_miu(self, X):index = np.random.choice(X.shape[0], 1, replace=False)mius = []mius.append(X[index])for _ in range(self.n_clusters - 1):max_dist_index = 0max_distance = 0for j in range(X.shape[0]):min_dist_with_miu = 999999for miu in mius:dist_with_miu = self.dist(miu, X[j])if min_dist_with_miu > dist_with_miu:min_dist_with_miu = dist_with_miuif max_distance < min_dist_with_miu:max_distance = min_dist_with_miumax_dist_index = jmius.append(X[max_dist_index])mius_array = np.array([])for i in range(self.n_clusters):if i == 0:mius_array = mius[i]else:mius[i] = mius[i].reshape(mius[0].shape)mius_array = np.append(mius_array, mius[i], axis=0)return mius_arraydef p(self, x, label):# self.mius_array[label] : [0.71841045 -1.22630378]# miu : [[ 0.71841045 -1.22630378]]miu = self.mius_array[label].reshape(1, -1)# 0.011842540821471443covdet = np.linalg.det(self.Sigma[label]) # 计算|cov| 行列式# [[0.1 0. ]# [0. 0.1]]covinv = np.linalg.inv(self.Sigma[label]) # 计算cov的逆if covdet < 1e-5: # 以防行列式为0covdet = np.linalg.det(# [[0.101 0. ]# [0. 0.101]]self.Sigma[label] + np.eye(x.shape[0]) * 0.001)covinv = np.linalg.inv(self.Sigma[label] + np.eye(x.shape[0]) * 0.001)# 0.7227907719753487a = np.float_power(2 * np.pi, x.shape[0] / 2) * np.float_power(covdet, 0.5)b = -0.5 * (x - miu) @ covinv @ (x - miu).Treturn 1 / a * np.exp(b)def pM(self, x, label):pm = 0for i in range(self.n_clusters):pm += self.Alpha[i] * self.p(x, i)return self.Alpha[label] * self.p(x, label) / pmdef update_miu(self, X, label):a = 0b = 0for i in range(X.shape[0]):a += self.Gamma[i][label] * X[i]b += self.Gamma[i][label]if b == 0:b = 1e-10return a / bdef update_sigma(self, X, label):a = 0b = 0for i in range(X.shape[0]):# [0.90345388 1.43013445]X[i] = X[i].reshape(1, -1)# [[ 0.9982843 -0.94389789]]# self.mius_array :# [[-0.81920702 -0.94646103]# [ 1.03198635 1.02942831]# [ 1.08892623 -1.0258301 ]]miu = self.mius_array[label].reshape(1, -1)a += self.Gamma[i][label] * \(X[i] - miu).T @ (X[i] - miu)b += self.Gamma[i][label]if b == 0:b = 1e-10sigma = a / breturn sigmadef update_alpha(self, X, label):a = 0for i in range(X.shape[0]):a += self.Gamma[i][label]return a / X.shape[0]def LL(self, X):ll = 0for i in range(X.shape[0]):before_ln = 0for j in range(self.n_clusters):before_ln += self.Alpha[j] * self.Gamma[i][j]ll += np.log(before_ln)return lldef fit(self, X):# [0.33333333 0.33333333 0.33333333]self.Alpha = np.array([1 / self.n_clusters] * self.n_clusters) # 初始化alphaself.mius_array = self.get_miu(X) # 初始化miu# sigma : (3,2,2)self.Sigma = np.array([np.eye(X.shape[1], dtype=float) * 0.1] * self.n_clusters) # 初始化sigma# gamma : (x.shape[0], 3)self.Gamma = np.zeros([X.shape[0], self.n_clusters])Y = np.zeros([X.shape[0]])iter = 0while (iter < self.max_iter):# init : 0old_ll = self.llfor i in range(X.shape[0]):for j in range(self.n_clusters):self.Gamma[i][j] = self.pM(X[i], j)for i in range(self.n_clusters):self.mius_array[i] = self.update_miu(X, i)self.Sigma[i] = self.update_sigma(X, i)self.Alpha[i] = self.update_alpha(X, i)self.ll = self.LL(X)print(self.ll)if abs(self.ll - old_ll) < 0.01:print('迭代{}次退出'.format(iter))breakiter += 1if iter == self.max_iter:print("迭代超过{}次,退出迭代".format(self.max_iter))for i in range(X.shape[0]):tmp_y = -1tmp_gamma = -1for j in range(self.n_clusters):if tmp_gamma < self.Gamma[i][j]:tmp_gamma = self.Gamma[i][j]tmp_y = jY[i] = tmp_yreturn Y
(5)标准互信息计算
# 标准化互信息
def NMI(A, B):# 样本点数total = len(A)A_ids = set(A)B_ids = set(B)# 互信息计算MI = 0eps = 1.4e-45for idA in A_ids:for idB in B_ids:idAOccur = np.where(A == idA)idBOccur = np.where(B == idB)idABOccur = np.intersect1d(idAOccur, idBOccur)px = 1.0 * len(idAOccur[0]) / totalpy = 1.0 * len(idBOccur[0]) / totalpxy = 1.0 * len(idABOccur) / totalMI = MI + pxy * math.log(pxy / (px * py) + eps, 2)# 标准化互信息Hx = 0for idA in A_ids:idAOccurCount = 1.0 * len(np.where(A == idA)[0])Hx = Hx - (idAOccurCount / total) * math.log(idAOccurCount / total + eps, 2)Hy = 0for idB in B_ids:idBOccurCount = 1.0 * len(np.where(B == idB)[0])Hy = Hy - (idBOccurCount / total) * math.log(idBOccurCount / total + eps, 2)MIhat = 2.0 * MI / (Hx + Hy)return MIhat
(6)匈牙利算法做标签映射
# 采用匈牙利算法处理标签
def processing_label(label, truth, n_clusters):# 指针为指向的向量的位置point = 0k = 0label_order = []# 标签矩阵,计算每个标签有多少位数字,然后再将相应标签打到相应位置label_matrix = np.zeros((n_clusters, n_clusters), np.int)for i in range(len(truth)):if truth[point] == truth[i]:continueelse:label_order.append(truth[point])counter = Counter(label[point:i])point = ifor j in range(n_clusters):label_matrix[k][j] = counter[j]k += 1label_order.append(truth[point])counter = Counter(label[point:len(label) - 1])for j in range(n_clusters):label_matrix[n_clusters - 1][j] = counter[j]# 得到每列的最优标签col_indrow_ind, col_ind = linear_sum_assignment(-label_matrix)# 标签的替换,先将0-9改换为10-19以免重复替换,在整体减10,得到最终结果for j in range(len(label)):for i in range(n_clusters):if label[j] == col_ind[i]:label[j] = label_order[i] + n_clustersreturn label - n_clusters
(7)精度计算
# 计算精确度
def ACC(y, pre_y):acc = np.sum(y[:] == pre_y[:])return acc / len(y)
三、手写函数进行聚类
from scipy.io import loadmat
from sklearn.mixture import GaussianMixturefrom model import KMeans
# from model import GaussianMixture
from model import LVQ, ACC, NMI, processing_label# 数据准备
minist_path = r".\datasets\MNIST.mat"
lung_path = r".\datasets\lung.mat"
yale_path = r".\datasets\Yale.mat"def classifications(path, n_clusters):data = loadmat(path)data_x = data["X"]data_y = data["Y"][:, 0]data_y -= 1# 预测kmeans_pre_y = KMeans(n_clusters=n_clusters).fit(data_x)kmeans_pre_y = processing_label(kmeans_pre_y, data_y, n_clusters)print('-----------')# print(kmeans_pre_y)# print(data_y)# print('-----------')# 得到簇中心lvq = LVQ()lvq.fit(data_x, data_y)lvq_mus = lvq.mus_arrayprint("学习向量量化原型向量:")print(lvq_mus)# gm_pre_y = GaussianMixture(n_clusters=n_clusters).fit(data_x)gm_pre_y = GaussianMixture(n_components=n_clusters).fit(data_x).predict(data_x)gm_pre_y = processing_label(gm_pre_y, data_y, n_clusters)# 精度kmeans_acc = ACC(data_y, kmeans_pre_y)gm_acc = ACC(data_y, gm_pre_y)print("kmeans_acc:")print(kmeans_acc)print("gm_acc:")print(gm_acc)# 标准互信息kmeans_nmi = NMI(data_y, kmeans_pre_y)mg_nmi = NMI(data_y, gm_pre_y)print("kmeans_nmi: ")print(kmeans_nmi)print("mg_nmi: ")print(mg_nmi)if __name__ == '__main__':print("minist: ")classifications(minist_path, 10)print('----------------------')print("yale: ")classifications(yale_path, 15)print('----------------------')print("lung: ")classifications(lung_path, 5)四、sklearn官方函数
from scipy.io import loadmat
from sklearn import metrics
# 可以使用sklearn官方的函数进行对比
from sklearn.cluster import KMeans
from sklearn.mixture import GaussianMixture# from model import GaussianMixture
# from model import KMeans
from model import LVQ, ACC, processing_label# 数据准备
minist_path = r".\datasets\MNIST.mat"
lung_path = r".\datasets\lung.mat"
yale_path = r".\datasets\Yale.mat"def NMI(y, pre_y):return metrics.normalized_mutual_info_score(y, pre_y)def classifications(path, n_clusters):data = loadmat(path)data_x = data["X"]data_y = data["Y"][:, 0]data_y -= 1# 预测# kmeans_pre_y = KMeans(n_clusters=n_clusters).fit(data_x)kmeans_pre_y = KMeans(n_clusters=n_clusters).fit(data_x).predict(data_x)kmeans_pre_y = processing_label(kmeans_pre_y, data_y, n_clusters)# 得到簇中心lvq = LVQ()lvq.fit(data_x, data_y)lvq_mus = lvq.mus_arrayprint("学习向量量化原型向量:")print(lvq_mus)# gm_pre_y = GaussianMixture(n_clusters=n_clusters).fit(data_x)gm_pre_y = GaussianMixture(n_components=n_clusters).fit(data_x).predict(data_x)gm_pre_y = processing_label(gm_pre_y, data_y, n_clusters)# 精度kmeans_acc = ACC(data_y, kmeans_pre_y)gm_acc = ACC(data_y, gm_pre_y)print("kmeans_acc:")print(kmeans_acc)print("gm_acc:")print(gm_acc)# 标准互信息kmeans_nmi = NMI(data_y, kmeans_pre_y)mg_nmi = NMI(data_y, gm_pre_y)print("kmeans_nmi: ")print(kmeans_nmi)print("gm_nmi: ")print(mg_nmi)if __name__ == '__main__':print("minist: ")classifications(minist_path, 10)print('----------------------')print("yale: ")classifications(yale_path, 15)print('----------------------')print("lung: ")classifications(lung_path, 5)五、结果:
(1)acc结果对比
| 数据/方法 | kmeans | GaussianMixture |
|---|---|---|
| minist | 0.527 | 0.486 |
| lung | 0.818 | 0.803 |
| yale | 0.358 | 0.429 |
(2)nmi结果对比
| 数据/方法 | kmeans | GaussianMixture |
|---|---|---|
| minist | 0.476 | 0.470 |
| lung | 0.6738 | 0.623 |
| yale | 0.471 | 0.478 |
(3)结果分析
- 通过实验可以发现由于lung数据集的数据量最大,标签类别只有5,因此每一类标签的训练数据集较大,因此结果较高,可以到百分之八十,yale数据量小,标签类别为15,因此每一类标签的训练数据集较小,结果也相对较差。可以通过优化模型,或者增加数据记得方式来提高精确度。
- 手写函数和sklearn的官方函数结果较为相似,除了速度稍慢以外,在实现书写体函数的过程中,加深了对函数的理解。
(4)控制台输出
- 由于没有计算lvq的精确度,因此,此处展示控制台输出。
minist:
迭代超过2000次,退出迭代
学习向量量化原型向量:
[[0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.]...[0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.]]
kmeans_acc:
0.527
gm_acc:
0.48633333333333334
kmeans_nmi:
0.4763899043312829
gm_nmi:
0.4706504060176245
----------------------
yale:
迭代5次退出
学习向量量化原型向量:
[[255 255 253 ... 254 255 255][ 25 21 18 ... 68 64 109][ 43 40 33 ... 19 23 87]...[ 25 32 43 ... 255 255 255][ 74 71 64 ... 254 253 164][ 45 35 45 ... 73 91 102]]
kmeans_acc:
0.3575757575757576
gm_acc:
0.41818181818181815
kmeans_nmi:
0.4715733810737053
gm_nmi:
0.47861216152317887
----------------------
lung:
迭代12次退出
学习向量量化原型向量:
[[3.91575578 1.10881254 1.49984291 ... 1.92498148 1.89642299 2.3734455 ][3.85497049 2.50536878 2.44310255 ... 0.95723516 2.51064914 2.21110052][3.87372448 1.17609126 1.3933997 ... 2.28305234 2.32255006 2.09166696][3.75517256 1.60927417 1.60927417 ... 1. 2.36144451 1.92515733][3.84942538 1.88691301 1.82792744 ... 1.4540376 2.46989679 2.07126504]]
kmeans_acc:
0.8177339901477833
gm_acc:
0.8029556650246306
kmeans_nmi:
0.6733520782350858
gm_nmi:
0.6235533750594885
这篇关于kmeans,学习向量量化lvq,高斯聚类函数GaussianMixture的python实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






