浅谈在操控器类中，为何要通过osgGA::CameraManipulator的逆矩阵改变视点位置

本文主要是介绍浅谈在操控器类中，为何要通过osgGA::CameraManipulator的逆矩阵改变视点位置，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在osg代码目录下的include\osgGA目录存放了很多osg自带的操控器类，这些操控器类都派生自osgGA::CameraManipulator，而这个CameraManipulator又派生自osgGA::GUIEventHandler，可见其本质上是个事件处理类。因此它首先会接收事件，比如鼠标一拖，场景就动。场景动与不动是受视点的位置、朝向来决定的，也就是观察矩阵，因此CameraManipulator必有处理事件的接口和输出矩阵的接口，处理事件的接口是函数bool handle(const osgGA::GUIEventAdapter& ea,osgGA::GUIActionAdapter &aa);所以每个操作器类必须要对这个函数大书特书来达到按自己的操作目的。这个handle的被调用的地方是在一帧绘制的事件遍历阶段，是在void Viewer::eventTraversal()中，viewer.cpp的第1125行（以osg 3.6.2为例，下同）：

_cameraManipulator->handle( event, 0, _eventVisitor.get());

虽然入参不一样，但是跟踪一下会发现会调用过去的。事件处理之后，就要根据处理的事件改变视点位置来达到操作场景的目的。这个是通过osgGA::CameraManipulator的如下函数：

virtual osg::Matrixd getInverseMatrix()

来实现的，它的调用时机是在更新阶段void Viewer::updateTraversal()中，viewer.cpp的第1212行：

_cameraManipulator->updateCamera(*_camera);

它会调用至：

camera.setViewMatrix(getInverseMatrix());

这个时候就有人不明白了，为什么要使用逆矩阵呢？原因这里有点绕，大家认真理解一下，世界坐标下，一个盒子在A点(xa,ya,za)，视点在B点（xb,yb,zb)，先不管朝向不朝向的。我们要输出此时在B点的人看到A点的图像，做法有很多，实际上图形学界是这么做的：把A点先转换为以B点为局部坐标的坐标系下，然后再进行一系列操作。这个变换的过程其实相当于需要求出把B点移回世界坐标原点的矩阵，A点再乘以这个矩阵就可以，这个移回的矩阵是这样计算的，把人从世界坐标原点移到B点的变换是Matrix，而把B点移回世界坐标原点的变换就是InverseMatrix，现在我们要把A点放在以B点为局部坐标下，则需要变换的就是InverseMatrix。下图是以二维坐标来讲解：（三维不好画出第三个轴，其实原理都一样）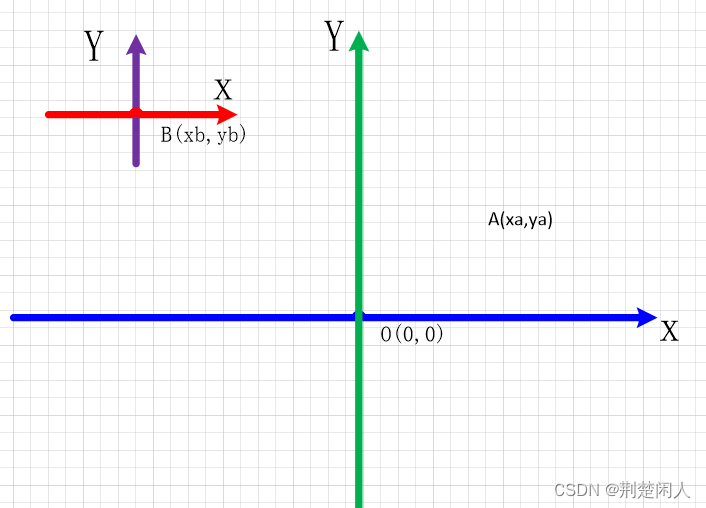

假设在世界坐标系XOY下，A点、B点的变换矩阵分别为MatrixA、MatrixB。如果以B点为原点的坐标系为基准，则原来的世界坐标系原点O的变换矩形则为 MatrixB的逆矩阵，记为InverseMatrixB。因为如果在以B点为原点的坐标系下，A点不能直接转到B坐标系下，必须通过世界坐标系转到B为原点的坐标系才行，即如果以B点为原点的坐标系为基准，则必须按B->O->A来算出A在B坐标系下的坐标。而A点在世界坐标下的变换矩阵为MatrixA(即对应O->A), 世界坐标系的原点O在以B点为原点的坐标系下的变换矩阵为InverseMatrixB(即对应B->O)，那么这反应到数学上，就是矩阵的级联相乘，即为如下：