本文主要是介绍约束优化算法(optimtool.constrain),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
import optimtool as oo
from optimtool.base import np, sp, plt
pip install optimtool>=2.4.2
约束优化算法(optimtool.constrain)
import optimtool.constrain as oc
oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初始迭代点])
import optimtool.constrain as oc
f, x1, x2 = sp.symbols("f x1 x2")
f = (x1 - 2)**2 + (x2 - 1)**2
c1 = x1 - x2 - 1
c2 = 0.25*x1**2 - x2 - 1
等式约束(equal)
oc.equal.[函数名]([目标函数], [参数表], [等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadratice(funcs: FuncArray, args: FuncArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=2, epsk: float=1e-4, epsilon: float=1e-4, k: int=0) -> OutputType | 增加二次罚项 |
| lagrange_augmentede(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, lamk: float=6, sigma: float=10, p: float=2, etak: float=1e-4, epsilon: float=1e-6, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.equal.penalty_quadratice(f, (x1, x2), c1, (1, 0.5), verbose=True)
(1, 0.5) 1.25 0
[2. 1.] 4.930380657631324e-32 1
(1.9999999999999998, 1.0) 4.930380657631324e-32 2
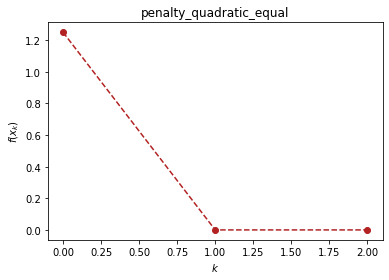
((1.9999999999999998, 1.0), 2)
不等式约束(unequal)
oc.unequal.[函数名]([目标函数], [参数表], [不等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadraticu(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=0.4, epsk: float=1e-4, epsilon: float=1e-10, k: int=0) -> OutputType | 增加二次罚项 |
| lagrange_augmentedu(funcs: FuncArray, args: ArgArray, cons: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, muk: float=10, sigma: float=8, alpha: float=0.2, beta: float=0.7, p: float=2, eta: float=1e-1, epsilon: float=1e-4, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.unequal.lagrange_augmentedu(f, (x1, x2), c2, (1.5, 0.5), verbose=True)
(1.5, 0.5) 0.5 0
(1.5, 0.5) 0.5 1
[2. 1.] 0.0 2
(2.0, 1.0) 0.0 3
(2.0, 1.0) 0.0 4
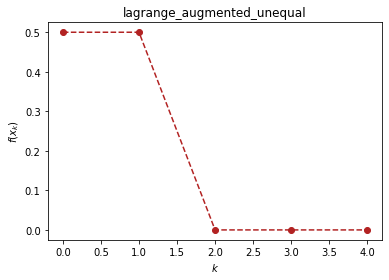
((2.0, 1.0), 4)
混合等式约束(mixequal)
oc.mixequal.[函数名]([目标函数], [参数表], [等式约束表], [不等式约束表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| penalty_quadraticm(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=10, p: float=0.6, epsk: float=1e-6, epsilon: float=1e-10, k: int=0) -> OutputType | 增加二次罚项 |
| penalty_L1(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, sigma: float=1, p: float=0.6, epsk: float=1e-6, epsilon: float=1e-10, k: int=0) -> OutputType | L1精确罚函数法 |
| lagrange_augmentedm(funcs: FuncArray, args: ArgArray, cons_equal: FuncArray, cons_unequal: FuncArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“newton”, lamk: float=6, muk: float=10, sigma: float=8, alpha: float=0.5, beta: float=0.7, p: float=2, eta: float=1e-3, epsilon: float=1e-4, k: int=0) -> OutputType | 增广拉格朗日乘子法 |
oc.mixequal.penalty_L1(f, (x1, x2), c1, c2, (1.5, 0.5), verbose=True)
(1.5, 0.5) 0.5 0
[2.5 0.5] 0.5 1
[1.47826087 1.6 ] 0.6322117202268434 2
[2.18 0.82] 0.06480000000000004 3
[1.892 1.108] 0.023328000000000043 4
[2.0648 0.9352] 0.008398079999999992 5
[1.96112 1.03888] 0.003023308800000004 6
[2.023328 0.976672] 0.001088391167999991 7
[1.9860032 1.0139968] 0.00039182082047999555 8
[2.00839808 0.99160192] 0.000141055495372801 9
[1.99496115 1.00503885] 5.0779978334209926e-05 10
[2.00302331 0.99697669] 1.8280792200315036e-05 11
[1.99818601 1.00181399] 6.581085192114058e-06 12
[2.00108839 0.99891161] 2.369190669160674e-06 13
[1.99934697 1.00065303] 8.529086408979587e-07 14
[2.00039182 0.99960818] 3.0704711072324775e-07 15
[1.99976491 1.00023509] 1.105369598604005e-07 16
[2.00014106 0.99985894] 3.9793305549762975e-08 17
(2.000141055495373, 0.9998589445046272) 3.9793305549762975e-08 18
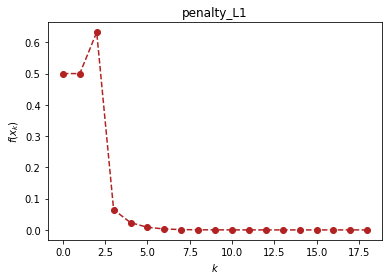
((2.000141055495373, 0.9998589445046272), 18)
这篇关于约束优化算法(optimtool.constrain)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








