数据结构基础详解(C语言): 二叉树的遍历_线索二叉树_树的存储结构_树与森林详解

本文主要是介绍数据结构基础详解(C语言): 二叉树的遍历_线索二叉树_树的存储结构_树与森林详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文逻辑:
本文由二叉树的遍历起手，讲解了二叉树的三种遍历方式，以及如何构造一颗二叉树，并在此基础上，扩展了更好的二叉树-线索二叉树。树和森林的存储结构讲解中，重点就是将树与森林转换为二叉树，这样二叉树的手段就能使用到树与森林当中。最后，讲解了二叉树与森林的遍历。

1.二叉树的遍历

什么是遍历
遍历：按照某种次序把所有的结点都访问一遍
什么是层次遍历：基于树的层次特性确定的次序规则（从上到下，从左到右的遍历）

二叉树的递归特性：
1️⃣ 要么是个空二叉树
2️⃣ 要么就是由根节点+左子树+右子树 组成的二叉树

1.1 二叉树的前,中,后序遍历

二叉树有三种遍历的情形
1️⃣先序遍历：根左右
2️⃣中序遍历：左根右
3️⃣ 后序遍历：左右根

二叉树的遍历(手算）

给你一个二叉树，写出他的先序遍历，中序遍历，后序遍历，属于简单题
给出一个手算技巧，留出空，根据遍历规则，补全

1.2 二叉树的层次遍历

• 算法思想
  1️⃣ 初始化一个辅助队列
  2️⃣ 根结点入队
  3️⃣ 若队列为空，则头结点出队。将其左孩子，右孩子插入队尾（如果有的话
  4️⃣ 重复3️⃣直至队列为空

1.3构造二叉树

直接说结论：
想要构造一个二叉树，必须知道的两种遍历序列，其中还必须有中序遍历。
也就是中序遍历+（前序遍历or后序遍历or层次遍历）

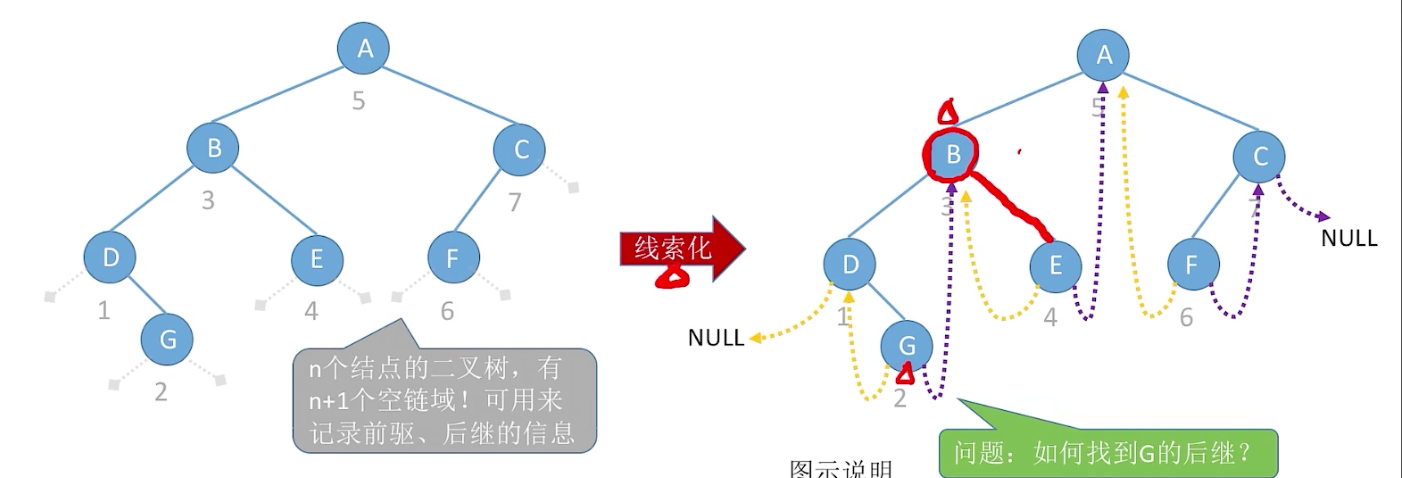
线索二叉树引入：

在二叉树的基础上，我们能否从一个指定结点开始中序遍历？
如何找到指定结点p在中序遍历序列中的前驱
如何找到p的中序后继
解决思路：
两个指针+目标结点p
从根节点出发，重新进行一次中序遍历，指针q记录当前访问的结点，指针pre记录上一个被访问的结点
当qp时，pre为前驱
当prep时，q为后继。
通过这种方法解决还是太麻烦了，所以引入线索二叉树

2.线索二叉树

2.1 以中序线索二叉树为例，讲解线索二叉树

n个结点的二叉树，有n+1个空链域，用来构成线索，记录前驱和后继

• 前驱线索（由左孩子指针充当）
• 后继线索（由右孩子指针充当）
  

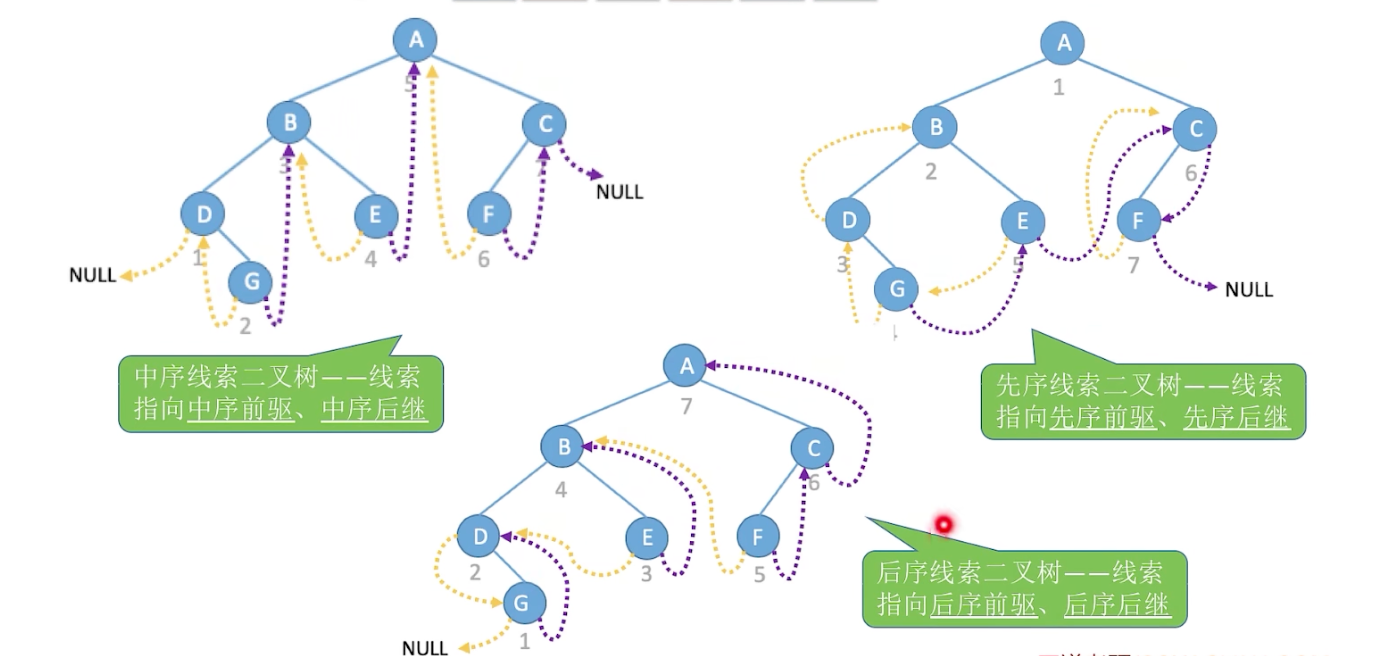
三种线索二叉树的对比

2.2 二叉树的线索化

为了区分指针是指向了孩子还是指向了前驱/后继
我们还需要两个标志 一个是ltag，一个是rtag，记录当前结点是否记录了线索

• ltag=0，lchild指向左孩子
• ltag=1，lchild指向前驱
• rtag=0，lchild指向右孩子
• rtag=1，lchild指向后继

一棵二叉树的中序线索化：
1.首先取得二叉树的中序序列，
假设是A₄,A₂,A₅,A₁,A₆,A₃
2.A₄的前驱指针指向NULL，A₃的后继指针指向NULL
3.遍历一遍树，如果左指针为空就指向前驱，如果右指针为空就指向后继。

2.3 线索二叉树中找前驱后继

2.3.1 中序线索二叉树寻找前驱后继(重点)

中序线索二叉树找中序后继

明确p点肯定有右孩子，没有右孩子的话，中序后继直接为NULL了
根据左根右，他的后继是右，也就是右子树，右孩子如果还有孩子，那继续左根右，即首先访问最左的点
综上所述，中序后继=p的右子树中最左下结点。

中序线索二叉树找中序前驱
有了之前的分析过程，很好推出，中序前驱=p的左子树中最右下结点

2.3.2 先序线索二叉树寻找前驱后继(了解)

先序线索二叉树找先序前驱
无法实现，除非土办法遍历或者，使用三叉链表（能找到p结点的父结点）
下面假设可以找到p的父节点.

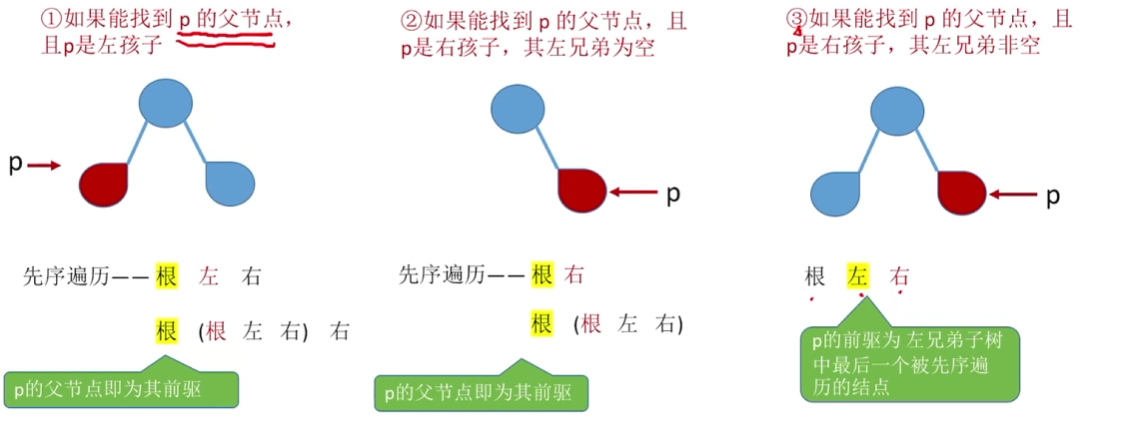
先序线索二叉树找先序后继
先序后继就是最左的节点

2.3.3 后序线索二叉树寻找前驱后继(了解)

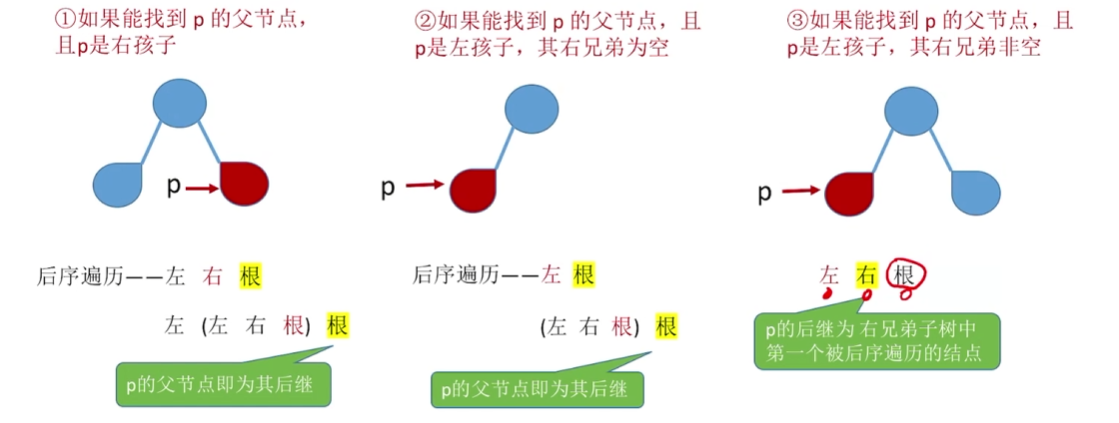
后序线索二叉树寻找后序前驱
p肯定有左孩子,若p有右孩子,则后序前驱是他的右孩子,没有就是左孩子

后序线索二叉树寻找后序后继
无法实现，除非土办法遍历或者，使用三叉链表（能找到p结点的父结点）
下面假设可以找到p的父节点.

3.树的存储结构

• 双亲表示法(顺序存储）
• 孩子表示法（顺序+链式存储）
• ⭐️孩子兄弟表示法(链式存储）

3.1 双亲表示法(顺序存储）

核心：每个结点中保存指向双亲的指针

增删改查思路：
增加一个孩子，直接在顺序的数组中增加即可
删除一个孩子，会让某一块为空，可以让最后一个存储的孩子，覆盖上去，提高效率
查找的话：想要找到某个结点的孩子，比较麻烦，要全部遍历一遍树

优缺点：
优点：查指定结点的双亲很方便。
缺点：查指定结点的孩子只能从头遍历。

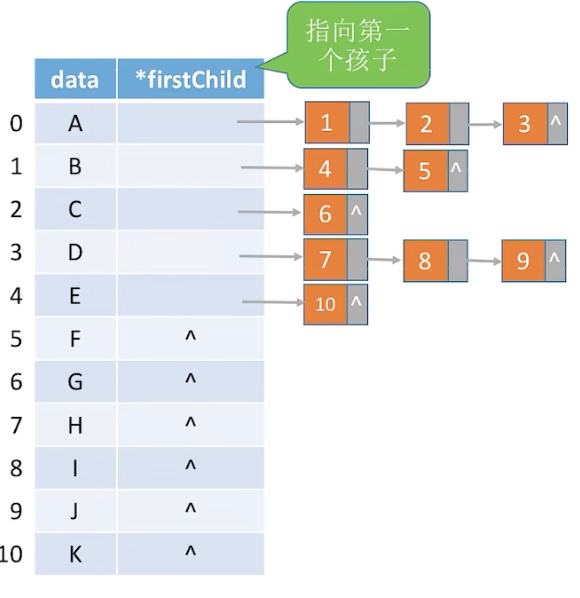
3.2 孩子表示法（顺序+链式存储）

核心：结点顺序存储，每一个结点的孩子，用链式存储

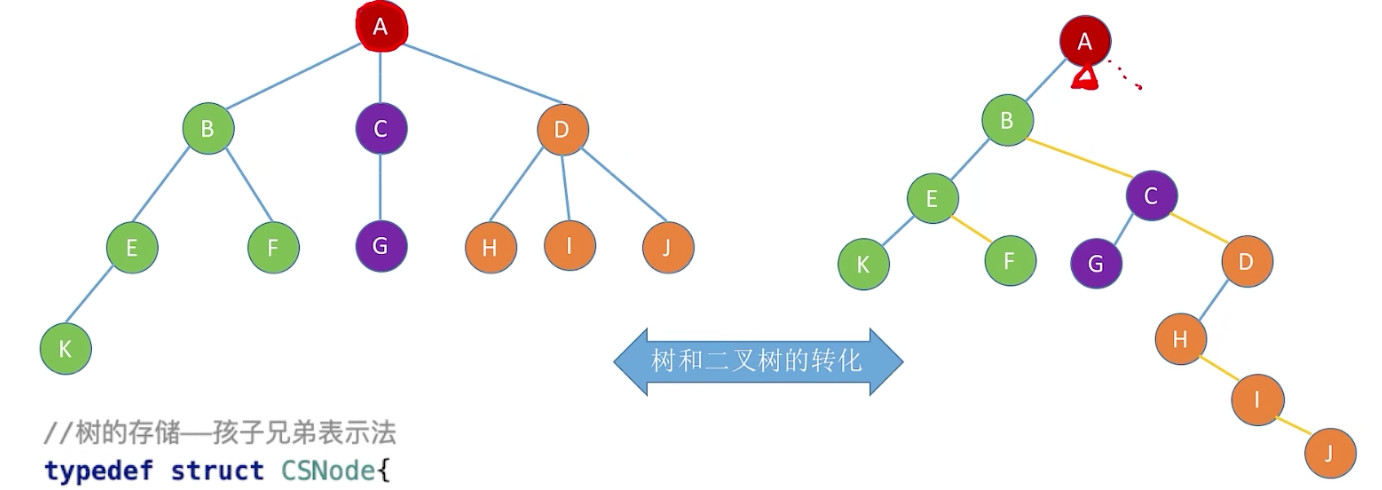
3.3 孩子兄弟表示法(链式存储）->重点

核心目的：将逻辑结构树能够转换为存储结构是二叉树的形式储存，这样我们就可以用处理二叉树的手段，处理它。

核心思路：左指针指向第一个孩子(最左边的孩子)，右指针指向他的右兄弟

我们可以 轻松的将一个树改写成这种孩子兄弟表示法的形式

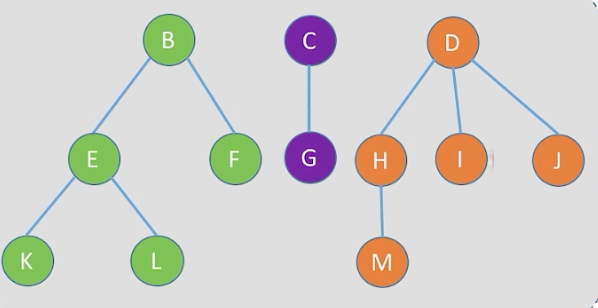
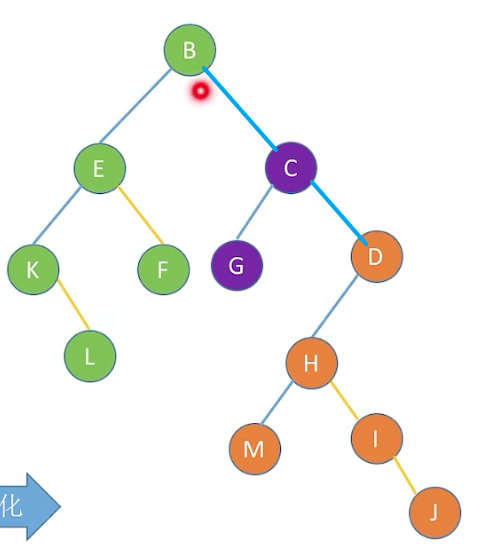
3.4 森林和二叉树的转换

在3.3的基础上，我们不难理解森林和二叉树的转换，就是按照孩子兄弟表示法

4.树的遍历

• 树的先根遍历

4.1 树的先根遍历（先根，先根，就是先遍历根，再遍历子树）

核心：先根遍历。若树非空，先访问根结点，再依次对每棵子树进行先根遍历。

与二叉树遍历对比：树的先根遍历序列与二叉树的先序遍历相同

4.2 树的后根遍历

核心：后根遍历。若树非空，先依次对每棵子树进行后根遍历，最后访问根结点
与二叉树遍历对比：树的后根遍历序列与二叉树的中序遍历相同

4.3 树的层次遍历

跟二叉树的层次遍历一样，用队列实现

5.森林的遍历

森林是m棵互不相交的树的集合。每棵树去掉根节点，其各个子树又组成森林。

5.1 先序遍历森林

若森林为非空，则按如下规则进行遍历；
访问森林中第一棵树的根结点。
先序遍历第一棵树中根结点的子树森林
先序遍历除去第一棵之后剩余的树构成的森林。

与树的遍历对比：效果等同于依次对各个树进行先根遍历

5.2 中序遍历森林

若森林为非空，则按如下规则进行遍历
中序遍历森林中第一棵树的根结点的子树森林
访问第一棵树的根结点。
中序遍历除去第一棵树之后剩余的树构成的森林。

与树的遍历对比：效果等同于依次对各个树进行后根遍历

这篇关于数据结构基础详解(C语言): 二叉树的遍历_线索二叉树_树的存储结构_树与森林详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---