本文主要是介绍2024高教社杯全国大学生数学建模竞赛B题保姆级分析完整思路+代码+数据教学,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2024高教社杯全国大学生数学建模竞赛 B题保姆级分析完整思路+代码+数据教学
B题题目:农作物的种植策略

接下来我们将按照题目总体分析-背景分析-各小问分析的形式来
1 总体分析
题目提供了一个电子产品生产的案例,要求参赛者建立数学模型解决企业在生产过程中的一系列决策问题。以下是对题目的总体分析:
问题一需要企业需要从供应商购买零配件,并且需要设计一个抽样检测方案,来决定是否接受供应商提供的零配件。题目要求设计一个能够尽可能减少检测次数的方案,分别在95%和90%的置信度下,判断零配件的次品率是否超过标称值。这个问题的核心是基于统计学的抽样检验,涉及假设检验和置信区间的计算。需要考虑标称值为10%的情况下,如何设计抽样数量,使得在满足不同置信水平的条件下进行接收或拒收决策。
问题二则:在生产过程中,企业需要在多个阶段做出决策,包括:
-
是否对零配件进行检测。
-
是否对成品进行检测。
-
是否对不合格的成品进行拆解,决定是否将拆解后的零配件重新利用。
-
如何处理用户退回的不合格产品。
需要根据这些参数为企业提供决策依据,并且给出相应的指标结果。
问题3:扩展的生产决策问题
在问题2的基础上,问题3进一步扩展了生产过程,增加了多个零配件和工序的情况。题目提供了多达8个零配件和2道工序的组装过程,要求针对更复杂的生产流程给出具体的决策方案。这部分问题的复杂度更高,可能涉及到多阶段决策和动态规划。
问题4:基于抽样检测的决策调整
假设问题2和问题3中的次品率均通过抽样检测得到,要求重新进行生产过程中的决策。这一问题要求参赛者结合问题1中的抽样检测方法,重新审视生产流程中的决策,可能需要重新设计检测方案,优化成本和风险的平衡。
问题2和问题3中的各个决策环节都涉及到成本效益的权衡,需要建立一个数学模型来综合考虑检测成本、拆解费用、次品率、调换损失等。
动态规划或优化模型:面对问题3中的多工序、多零配件的复杂情况,可以使用动态规划或其他优化方法,来寻找到最优的决策路径。
2 背景分析
总结一下,题目的背景集中在生产过程中的质量控制和成本优化,企业需要在多个决策点上进行权衡,既要保证最终产品的质量,又要尽量减少生产和处理的成本损失。
3 各小问分析
这道题目是关于生产过程中的决策问题,涉及到电子产品制造中的抽样检测、装配、拆解、退换货等多个环节。问题分为四个主要部分,要求为企业设计优化生产决策的数学模型。
问题1:抽样检测方案建模与分析
该问题要求设计一个抽样检测方案,判断零配件的次品率是否超过标称值。在这个问题中,零配件次品率不会超过某个标称值(如10%)。我们需要在不同信度下,决定是否接受这批零配件。
建模目标:
我们需要设计一个抽样检测方案,确保:
1.在95%的信度下,判断零配件次品率超过标称值时拒收该批次零配件。
2.在90%的信度下,判断零配件次品率不超过标称值时接收该批次零配件。
1.抽样检测方案的基础理论
-
假设检验 我们可以使用假设检验来进行模型设计。设: p为零配件的真实次品率。 p0为标称的次品率(10%)。 我们抽取的样本数为n,次品数为x。 根据问题要求,我们可以构建两个假设: 原假设H_0:零配件次品率p\leq p_0(零配件次品率不超过标称值,接受零配件)。 备择假设H_1:零配件次品率p>p_0(零配件次品率超过标称值,拒绝零配件)。
-
二项分布建模 对于每个零配件,若其合格率为1-p,则每个零配件是次品的概率为p。假设我们从一批零配件中抽取了n个样本,次品的数量服从二项分布:
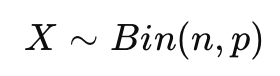
其中: n是抽样数量。 p是次品率。 X是次品的个数。 可以用正态分布近似二项分布:
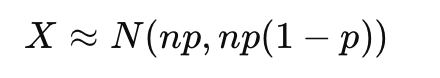
通过正态近似,可以使用标准化公式:
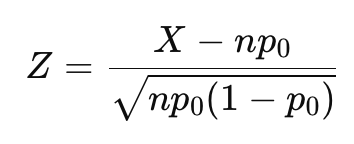
-
双侧检验与置信区间
我们根据问题中95%和90%的信度要求进行双侧假设检验。信度要求分别对应的显著性水平alpha为:
95%信度:对应alpha=0.05。
90%信度:对应alpha=0.10。
在这两种情况下,分别计算不同显著性水平下的拒收与接收条件。
2.具体建模步骤
-
第一种情况:拒收零配件(95%信度) 我们希望设计一个方案,使得在95%信度下,认定次品率超过标称值时拒收该批零配件。 显著性水平alpha=0.05,对应的临界值Z_{\alpha/2}=1.96。 原假设为\(p=p_0=0.10\)(即零配件次品率为10%)。 拒收条件是当样本中检测出的次品率
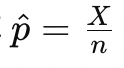
足够大时,我们拒收这批零配件。 标准化变量为:
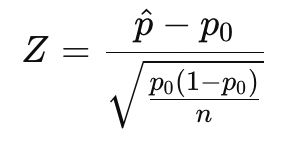
拒收条件为:
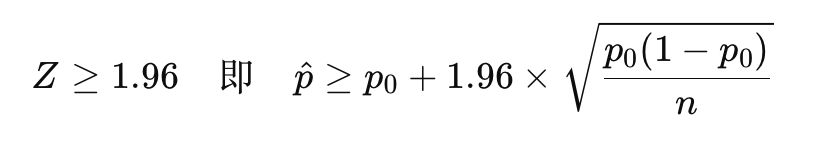
将p0=0.10代入,得到拒收条件:

通过这个公式,我们可以根据抽样的数量n得到拒收条件。
-
第二种情况:接收零配件(90%信度) 我们希望在90%信度下,判断零配件的次品率不超过标称值时接收这批零配件。 显著性水平alpha=0.10,对应的临界值Z_{\alpha/2}=1.645。 接收条件是次品率hat{p}足够低。 接收条件为:
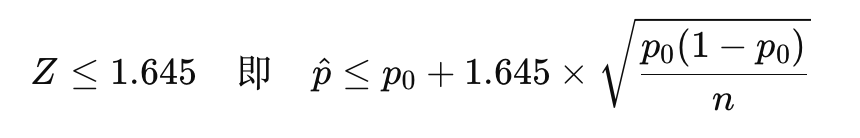
将p0=0.10代入,得到接收条件:
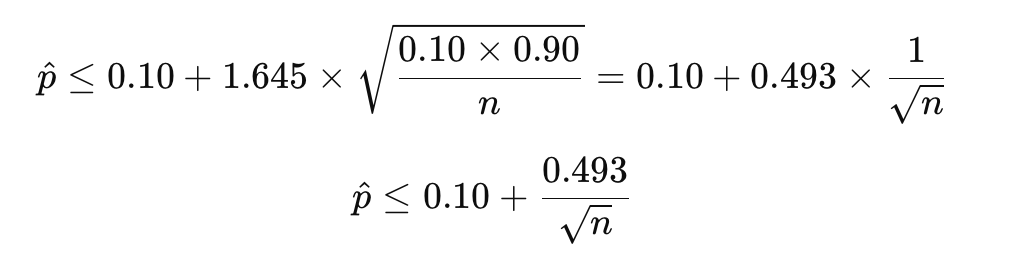
-
确定最小抽样数量n
为了满足两种信度要求,我们可以根据上面的拒收和接收条件,计算不同情况下的最小抽样量\(n\)。
问题2:生产过程的决策建模
问题2的主要任务是对生产过程中的多个环节进行决策,优化每个阶段的检测、装配、拆解及不合格品处理,最终使得企业的总成本最小化或收益最大化。主要涉及零配件的检测、成品的检测、拆解和调换不合格品等多项决策。
根据题目描述,企业需要从成本和收益的角度优化生产过程的每个阶段。建模目标是:
- 最小化总成本(包括检测成本、装配成本、拆解费用、调换损失等)。
- 同时考虑成品的次品率及市场售价,确保利润最大化。
设定以下变量用于模型:
p_1, p_2 :零配件1和零配件2的次品率。
c_1, c_2 :零配件1和零配件2的购买单价。
d_1, d_2 :零配件1和零配件2的检测成本。
p_f :成品的次品率(由两个零配件的次品率决定,稍后说明计算方式)。
c_f :成品的装配成本。
d_f :成品的检测成本。
s_f :成品的市场售价。
t_f :调换不合格成品的损失。
e_f :拆解费用。
根据题目的描述,成品的次品率 由两个零配件的次品率决定:
- 若零配件1或零配件2中任一为次品,成品即为次品。因此,成品次品率为:
p_f = 1 - (1 - p_1)(1 - p_2)
该公式表明,只要零配件1或零配件2有任意一个不合格,则成品不合格。
成本函数的构建
接下来,我们需要根据生产过程的不同阶段构建相应的总成本函数。成本主要来自以下几个方面:
零配件检测与装配成本:
成品检测成本:
拆解成本:
对不合格成品的拆解费用为 \( e_f \),拆解后的零配件可重新使用。
调换不合格品的损失:
市场上的不合格品会引起退货和调换,损失为 \( n_f \cdot p_f \cdot t_f \)。
-
零配件检测决策
-
如果对零配件进行检测: - 总成本为:检测成本 + 购买零配件成本 + 装配成本
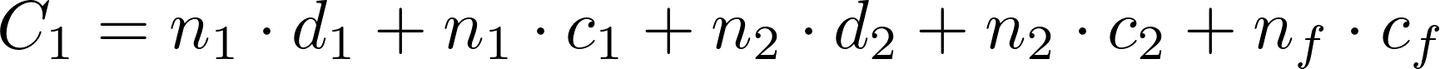
-
如果不检测零配件:
- 将不合格零配件直接进入装配,可能会产生成品不合格的额外成本。
(2) 成品检测决策
-
如果对成品进行检测: - 总成本为:检测成本 + 装配成本 + 不合格成品的拆解费用
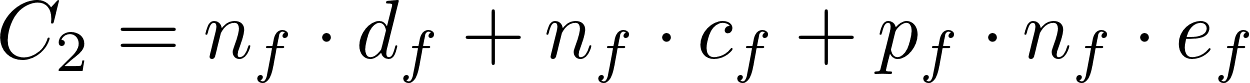
-
如果不检测成品:
- 市场上出售的次品成品将导致退货,产生调换损失:
剩余后续更新。
其中更详细的思路,各题目思路、代码、讲解视频、成品论文及其他相关内容,可以点击下方群名片哦!
这篇关于2024高教社杯全国大学生数学建模竞赛B题保姆级分析完整思路+代码+数据教学的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




