题解：CF 1200 F Graph Traveler

本文主要是介绍题解：CF 1200 F Graph Traveler，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Codeforces AC 提交记录

题意

有一张图，可重边可自环。行走规则：初始时有一个值 $c$ 和所在的点 $x$ ，到达一个点就将 $c$ 加上点权 $k_x$ ，每次可以走从点 $x$ 连出去的第 $c\%m_x$ 条边，到达下一个点。有 $q$ 个询问，给你 $x$ 和 $c$ ，问在行走过程中有几个点会经过无限次（如果从一个点能走到一个环，问这个环包含的点数；否则是 $0$ ）。

思路

$q$ 和 $y$ 都太大了，发现 $m_i$ 很小。 $y$ 对 $m_i$ 取模决定走到哪个点，可以先将 $y$ 对 $l c m (1, 2, 3, ..., 10)$ 取模。因为 $m_i$ 在 $1$ 到 $10$ 范围内，无论对哪个 $m_i$ ， $l c m (1, 2, 3, ..., 10)$ 都是它的倍数，所以不影响 $y$ 对每个 $m_i$ 取模的结果。
当前的值 $y$ 对于边是有影响的，遂将 $(x, y)$ 作为一个状态。 $l c m (1, 2, 3, ..., 10) = 2520$ ，那么状态数最多只有 $1000\times2520$ 种，只要用记忆化搜索处理出每种状态的答案，就可以 $O (1)$ 回答问题。

实现

由于 $x, y$ 确定，每种状态有固定的下一个状态： $tx=e_{x,y\%m_x},ty=y+k_{tx}$ 。我们用 $cnt_{x,y}$ 记录答案， $flag_{x,y}$ 记录这个状态在第几次 $df s$ （在 $main$ 函数里被调用第几次）的时候算到了。如果即将到达的状态的 $f l a g$ 是 $0$ ，就 $df s (t x, t y)$ ；如果 $f l a g$ 等于当前的次数，就证明这个环是新找到的，计算环里有几个点并赋值给 $cnt_{x,y}$ ；如果这个状态在之前的 $df s$ 中就已经计算过了，证明这个环已经被找到过了，直接 $cnt_{x,y}=cnt_{tx,ty}$ 。最后查询答案的时候要把 $x$ 的点权加进去，答案是 $cnt_{x,y+k_x}$ 。
过程中注意 $y$ 的取模，由于 $y$ 可能是负数， $y=(y\%2520+2520)\%2520$ 。计算环里点的个数时，要用 $v i s$ 标记一个点是否数过了，因为 $s t a c k$ 记录的只有 $x$ ，而状态里是 $(x, y)$ ，可能重复。
在下图中，原本的路径是黑色的，更新答案的路径是蓝色的：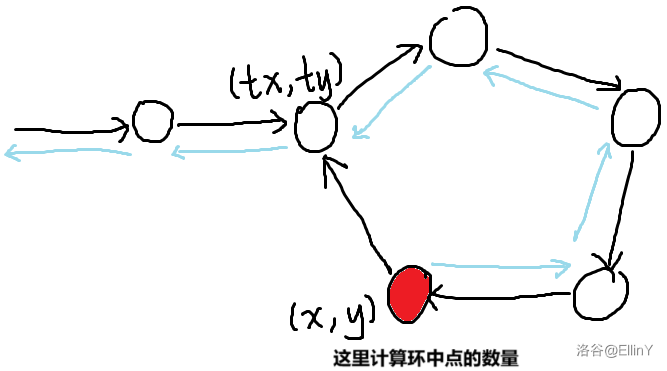

代码

#include<bits/stdc++.h>
using namespace std;
#define mod 2520
int n,k[1005],m[1005],e[1005][15],q,a,b;
int cnt[1005][2520],st[2520000],pos[1005][2520],flag[1005][2520];
bool vis[1005];
void mo(int& x){ x=(x%mod+mod)%mod; }
void dfs(int x,int y,int id){flag[x][y]=id;st[pos[x][y]]=x;int tx=e[x][y%m[x]];int ty=y+k[tx];mo(ty);if(!flag[tx][ty]){pos[tx][ty]=pos[x][y]+1,dfs(tx,ty,id);cnt[x][y]=cnt[tx][ty];}if(flag[tx][ty]==id){for(int i=pos[tx][ty];i<=pos[x][y];i++)vis[st[i]]=0;for(int i=pos[tx][ty];i<=pos[x][y];i++)if(!vis[st[i]]) vis[st[i]]=1,cnt[x][y]++;}else cnt[x][y]=cnt[tx][ty];
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&k[i]),mo(k[i]);for(int i=1;i<=n;i++){scanf("%d",&m[i]);for(int j=0;j<m[i];j++) scanf("%d",&e[i][j]);}int l=0;for(int i=1;i<=n;i++)for(int j=0;j<mod;j++)if(flag[i][j]==0) dfs(i,j,++l);scanf("%d",&q);for(int i=1;i<=q;i++){scanf("%d%d",&a,&b);b+=k[a];mo(b);printf("%d\n",cnt[a][b]);}return 0;
}