74.搜索二维矩阵

本文主要是介绍74.搜索二维矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

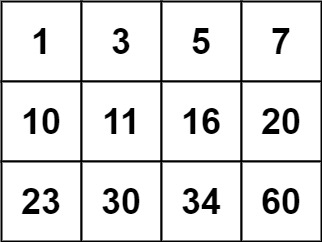
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

2.解题思路

首先通过二分查找找到target可能所在的行，找到满足首个元素< target的最后一行,因为只有最后一行是可能含有target的，例如[[1,2,3,4],[5,6,7,8]] target  = 7, 这两行首个元素都小于target,那么第一行的最后一个元素肯定是小于第二行的第一个元素的，因为第二行的第一个元素也小于target，所以target只可能出现在第二行中，因此我们只需要找到符合行首元素小于target的最后一行，然后再在这一行中使用二分查找找target即可，找到了就返回true,找不到就返回false

3.代码实现

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length;int n = matrix[0].length;int row_l = 0, row_r = m - 1;//首先找到target所在行while (row_l < row_r) {int row_mid = row_l + (row_r - row_l) / 2 + 1;if (target < matrix[row_mid][0]) {row_r = row_mid - 1;} else {row_l = row_mid;}}if (row_l < 0 || row_l >= m) {return false;}//row_l即为target可能位于的行int l = 0, r = n - 1;while (l <= r) {int mid = l + (r - l) / 2;if (matrix[row_l][mid] > target) {r = mid - 1;} else if (matrix[row_l][mid] < target) {l = mid + 1;} else {return true;}}return false;}
}

这篇关于74.搜索二维矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---