快速Fibonacci数，矩阵法

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_{n − 1} + F_{n − 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of F_n.

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

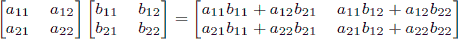Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

这个题是要用矩阵的知识解决斐波那契数列，题目中给的公式很简单，直接往上套就行了，那我们就先看除了题目给的方法外的另一个方法，当然还是矩阵。

先看下面的公式：

不难看出这个式子是把：

写成矩阵的形式而已。

将上面的式子迭代可得：

得一般式为：

继续展开会得到:

设：

则：

所以：

现在已经很明显了，其中还要用到矩阵快速幂的知识，代码如下：

#include <stdio.h>
#include <string.h>
#include <math.h>
typedef __int64 int64;int64 c[2][2],ans[2][2],d[2][2],a[2][2];int main()
{int64 i,j,n,k,t;while(scanf("%I64d",&n)!=EOF){if(n==-1)		break;if(n==0){printf("0\n");continue;}if(n==1){printf("1\n");continue;}memset(ans,0,sizeof(ans));for(i=0;i<2;i++)ans[i][i]=1;a[0][0]=a[0][1]=a[1][0]=1;a[1][1]=0;n=n-2;while(n!=0){if(n%2==1){memset(d,0,sizeof(d));				for(i=0;i<2;i++)for(j=0;j<2;j++)if(a[i][j])for(k=0;k<2;k++){d[i][k]+=ans[i][j]*a[j][k];		d[i][k]=d[i][k]%10000;}for(i=0;i<2;i++)for(j=0;j<2;j++)ans[i][j]=d[i][j];			}memset(c,0,sizeof(c));for(i=0;i<2;i++)for(j=0;j<2;j++){if(a[i][j]==0)continue;for(k=0;k<2;k++){c[i][k]+=a[i][j]*a[j][k]; c[i][k]=c[i][k]%10000;}}for(i=0;i<2;i++)for(j=0;j<2;j++)a[i][j]=c[i][j];n=n/2;}t=(ans[0][0]+ans[0][1])%10000;if(t==0)printf("0\n");else printf("%I64d\n",t);}return 0;
}

#include <stdio.h>
#include <string.h>
#include <math.h>
typedef __int64 int64;int64 c[2][2],ans[2][2],d[2][2],a[2][2];int main()
{int64 i,j,n,k,t;while(scanf("%I64d",&n)!=EOF){if(n==-1)		break;if(n==0){printf("0\n");continue;}if(n==1){printf("1\n");continue;}memset(ans,0,sizeof(ans));for(i=0;i<2;i++)ans[i][i]=1;a[0][0]=a[0][1]=a[1][0]=1;a[1][1]=0;while(n!=0){if(n%2==1){memset(d,0,sizeof(d));					for(i=0;i<2;i++)for(j=0;j<2;j++)if(a[i][j])for(k=0;k<2;k++){d[i][k]+=ans[i][j]*a[j][k];		d[i][k]=d[i][k]%10000;}for(i=0;i<2;i++)for(j=0;j<2;j++)ans[i][j]=d[i][j];				}memset(c,0,sizeof(c));for(i=0;i<2;i++)for(j=0;j<2;j++){if(a[i][j]==0)continue;for(k=0;k<2;k++){c[i][k]+=a[i][j]*a[j][k]; c[i][k]=c[i][k]%10000;}}for(i=0;i<2;i++)for(j=0;j<2;j++)a[i][j]=c[i][j];n=n/2;}if(ans[0][1]==0)printf("0\n");else printf("%I64d\n",ans[0][1]);}return 0;
}