本文主要是介绍8、AUTOGRAD MECHANICS,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本笔记将概述 autograd 如何工作并记录操作。 理解所有这些并不是绝对必要的,但我们建议熟悉它,因为它会帮助您编写更高效、更干净的程序,并可以帮助您进行调试。
How autograd encodes the history
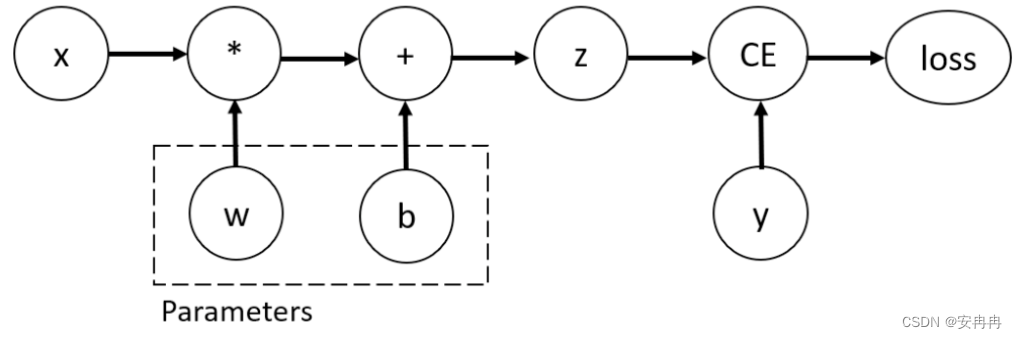
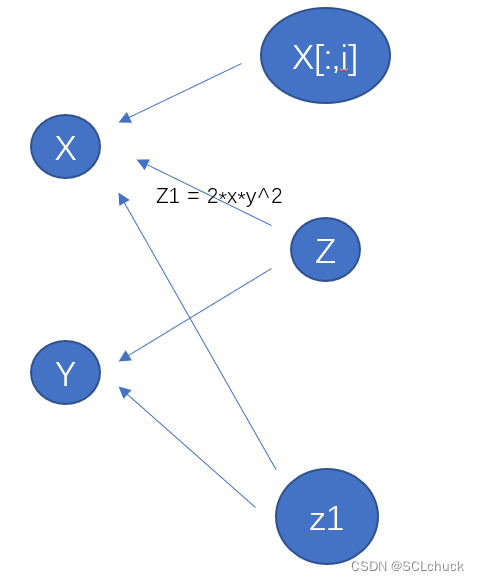
Autograd 是反向自动微分系统。 从概念上讲,autograd 会记录一个图形,记录在您执行操作时创建数据的所有操作,为您提供一个有向无环图,其叶子是输入张量,根是输出张量。 通过从根到叶跟踪此图,您可以使用链式法则自动计算梯度。
在内部,autograd 将此图表示为 Function 对象(实际上是表达式)的图,可以通过 apply() 来计算计算图的结果。 在计算前向传递时,autograd 同时执行请求的计算并构建一个表示计算梯度的函数的图(每个 torch.Tensor 的 .grad_fn 属性是该图的入口点)。 当前向传递完成后,我们在后向传递中评估该图以计算梯度。
需要注意的重要一点是,每次迭代都会从头开始重新创建图形,这正是允许使用任意 Python 控制流语句的原因,它可以在每次迭代时更改图形的整体形状和大小。 在开始训练之前,您不必对所有可能的路径进行编码 - 您运行的就是您所区分的。
Locally disabling gradient computation
Python 有多种机制可以在本地禁用梯度计算:
要在整个代码块中禁用梯度,有上下文管理器,如 no-grad 模式和推理模式。 为了从梯度计算中更细粒度地排除子图,可以设置张量的 requires_grad 字段。
下面,除了讨论上述机制之外,我们还描述了评估模式(nn.Module.eval()),该方法实际上并未用于禁用梯度计算,但由于其名称,经常与三种方法混淆 .
Setting requires_grad
requires_grad 是一个标志,允许从梯度计算中细粒度地排除子图。 它在向前和向后传递中都有效:
在前向传递期间,只有在其输入张量中至少有一个需要 grad 时,才会将操作记录在后向图中。 在向后传递 (.backward()) 期间,只有 requires_grad=True 的叶张量才会将梯度累积到它们的 .grad 字段中。
值得注意的是,即使每个张量都有这个标志,设置它只对叶张量有意义(没有 grad_fn 的张量,例如,一个 nn.Module 的参数)。 非叶张量(确实具有 grad_fn 的张量)是具有与之关联的后向图的张量。 因此,将需要它们的梯度作为中间结果来计算需要 grad 的叶张量的梯度。 从这个定义中,很明显所有非叶张量都会自动具有 require_grad=True。
设置 requires_grad 应该是您控制模型的哪些部分是梯度计算的一部分的主要方式,例如,如果您需要在模型微调期间冻结部分预训练模型。
要冻结模型的某些部分,只需将 .requires_grad_(False) 应用于您不想更新的参数。 如上所述,由于使用这些参数作为输入的计算不会记录在前向传递中,因此它们不会在后向传递中更新其 .grad 字段,因为它们不会成为第一个中的后向图的一部分 地方,根据需要。
因为这是一个很常见的模式,requires_grad 也可以使用 nn.Module.requires_grad_() 在模块级别设置。 当应用于模块时, .requires_grad_() 对模块的所有参数生效(默认情况下 requires_grad=True )。
Grad Modes
除了设置 requires_grad 之外,Python 还可以启用三种可能的模式,这些模式可以影响 autograd 在内部处理 PyTorch 中的计算的方式:默认模式(grad 模式)、no-grad 模式和推理模式,所有这些模式都可以通过上下文切换 管理者和装饰者。
Default Mode (Grad Mode)
“默认模式”实际上是当没有启用其他模式(如 no-grad 和推理模式)时我们隐含的模式。 与“无梯度模式”相比,默认模式有时也称为“梯度模式”。
关于默认模式最重要的一点是,它是 requires_grad 生效的唯一模式。 在其他两种模式下, requires_grad 总是被覆盖为 False 。
No-grad Mode
no-grad 模式下的计算表现得好像没有任何输入需要 grad。 换句话说,即使存在具有 require_grad=True 的输入,no-grad 模式下的计算也永远不会记录在向后图中。
当您需要执行不应由 autograd 记录的操作时启用 no-grad 模式,但您稍后仍希望在 grad 模式下使用这些计算的输出。 这个上下文管理器可以很方便地禁用代码块或函数的梯度,而不必临时将张量设置为 requires_grad=False,然后再设置为 True。
例如,在编写优化器时,no-grad 模式可能很有用:在执行训练更新时,您希望就地更新参数,而无需 autograd 记录更新。 您还打算在下一次前向传递中使用更新的参数进行 grad 模式的计算。
torch.nn.init 中的实现在初始化参数时也依赖于 no-grad 模式,以避免在就地更新初始化参数时自动梯度跟踪。
Inference Mode
推理模式是 no-grad 模式的极端版本。 就像在 no-grad 模式下一样,推理模式下的计算不会记录在后向图中,但启用推理模式将允许 PyTorch 进一步加速您的模型。 这种更好的运行时有一个缺点:在推理模式下创建的张量在退出推理模式后将无法用于由 autograd 记录的计算。
当您执行不需要在后向图中记录的计算时启用推理模式,并且您不打算在以后由 autograd 记录的任何计算中使用在推理模式中创建的张量。
建议您在不需要 autograd 跟踪的代码部分(例如,数据处理和模型评估)中尝试推理模式。 如果它为您的用例开箱即用,那么它就是免费的性能胜利。 如果在启用推理模式后遇到错误,请检查在退出推理模式后由 autograd 记录的计算中是否使用在推理模式下创建的张量。 如果在您的情况下无法避免这种使用,您可以随时切换回 no-grad 模式。
有关推理模式的详细信息,请参阅推理模式。
推理模型的实现细节见RFC-0011-推理模式。
Evaluation Mode (nn.Module.eval())
评估模式实际上并不是一种在本地禁用梯度计算的机制。 无论如何,它都包含在这里,因为它有时会被混淆为这样一种机制。
在功能上,module.eval()(或等效的 module.train())与 no-grad 模式和推理模式完全正交。 model.eval() 如何影响您的模型完全取决于您的模型中使用的特定模块以及它们是否定义了任何训练模式特定行为。
如果您的模型依赖于诸如 torch.nn.Dropout 和 torch.nn.BatchNorm2d 之类的模块,它们的行为可能因训练模式而异,例如,为了避免更新,则您负责调用 model.eval() 和 model.train() 您的 BatchNorm 运行统计数据验证数据。
建议您在训练时始终使用 model.train() 并在评估模型(验证/测试)时使用 model.eval(),即使您不确定您的模型是否具有特定于训练模式的行为,因为您正在使用的模块可能会更新为在训练和评估模式下表现不同。
In-place operations with autograd
在 autograd 中支持就地操作是一件困难的事情,我们不鼓励在大多数情况下使用它们。 Autograd 积极的缓冲区释放和重用使其非常高效,并且就地操作实际上很少显着降低内存使用量。 除非您在沉重的内存压力下运行,否则您可能永远不需要使用它们。
有两个主要原因限制了就地操作的适用性:
1、就地操作可能会覆盖计算梯度所需的值。
2、每个就地操作实际上都需要实现来重写计算图。 异地版本只是分配新对象并保留对旧图的引用,而就地操作需要更改表示此操作的函数的所有输入的创建者。 这可能很棘手,特别是如果有许多张量引用相同的存储(例如通过索引或转置创建),并且如果修改输入的存储被任何其他张量引用,就地函数实际上会引发错误。
In-place correctness checks
每个张量都有一个版本计数器,每当它在任何操作中被标记为脏时,它就会增加。 当函数为向后保存任何张量时,也会保存它们包含的张量的版本计数器。 一旦您访问 self.saved_tensors ,它就会被检查,如果它大于保存的值,则会引发错误。 这确保如果您使用就地函数并且没有看到任何错误,您可以确保计算出的梯度是正确的。
Multithreaded Autograd
autograd 引擎负责运行计算反向传播所需的所有反向操作。 本节将描述可以帮助您在多线程环境中充分利用它的所有细节。(这仅与 PyTorch 1.6+ 相关,因为之前版本的行为有所不同)。
用户可以使用多线程代码(例如 Hogwild 训练)训练他们的模型,并且不会阻塞并发向后计算,示例代码可以是:
# Define a train function to be used in different threads
def train_fn():x = torch.ones(5, 5, requires_grad=True)# forwardy = (x + 3) * (x + 4) * 0.5# backwardy.sum().backward()# potential optimizer update# User write their own threading code to drive the train_fn
threads = []
for _ in range(10):p = threading.Thread(target=train_fn, args=())p.start()threads.append(p)for p in threads:p.join()请注意,用户应该注意的一些行为:
Concurrency on CPU
当您在 CPU 上的多个线程中通过 python 或 C++ API 运行 reverse() 或 grad() 时,您希望看到额外的并发性,而不是在执行期间以特定顺序序列化所有向后调用(PyTorch 1.6 之前的行为)。
Non-determinism
如果您在多个线程上同时调用backward() 但使用共享输入(即Hogwild CPU 训练)。 由于参数是跨线程自动共享的,梯度累积可能在跨线程的反向调用时变得不确定,因为两个反向调用可能会访问并尝试累积相同的 .grad 属性。 这在技术上是不安全的,它可能会导致赛车状况,结果可能无法使用。
但是,如果您使用多线程方法来驱动整个训练过程但使用共享参数,那么这是预期的模式,使用多线程的用户应该牢记线程模型并应该期望这种情况发生。 用户可以使用功能 API torch.autograd.grad() 来计算梯度而不是 backward() 以避免不确定性。
Graph retaining
如果 autograd 图的一部分在线程之间共享,即运行前向单线程的第一部分,然后在多个线程中运行第二部分,则图的第一部分是共享的。在这种情况下,不同的线程在同一个图上执行 grad() 或 backward() 可能会在一个线程的运行中破坏图,而另一个线程在这种情况下会崩溃。Autograd 会向用户出错,类似于在不保留_graph=True 的情况下调用backward() 两次,并让用户知道他们应该使用retain_graph=True。
Thread Safety on Autograd Node
由于 Autograd 允许调用者线程驱动其向后执行以实现潜在的并行性,因此重要的是我们确保 CPU 上的线程安全与并行向后共享 GraphTask 的一部分/全部。
由于 GIL,自定义 Python autograd.function 是自动线程安全的。 对于内置 C++ Autograd 节点(例如 AccumulateGrad、CopySlices)和自定义 autograd::Function,Autograd 引擎使用线程互斥锁来保护可能具有状态写入/读取的 autograd 节点上的线程安全。
No thread safety on C++ hooks
Autograd 依赖于用户编写线程安全的 C++ 钩子。 如果您希望在多线程环境中正确应用钩子,则需要编写适当的线程锁定代码以确保钩子是线程安全的。
这篇关于8、AUTOGRAD MECHANICS的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!