【最长公共上升子序列】

本文主要是介绍【最长公共上升子序列】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

解决

for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j){  f[i][j] = f[i - 1][j];if (a[i] == b[j]){  f[i][j] = max(f[i][j], 1);for (int k = 1; k < j; ++k)if (b[j] > b[k])f[i][j] = max(f[i][j], f[i - 1][k] + 1);}  }

先假设 $a[i]$ 不影响结果，纳入 $f[i-1][j]$

（实际上 $a[i]$ 可能影响结果，在剩下的划分中考虑）

然后判断是否相同，如果相同，结合题设的 $b[j]$ 影响结果得出 $a[i]$ 对应 $b[j]$ ，此时长度至少为1

再通过枚举合法的“倒数第二个值” $b[k]$ 将答案进一步转移

（一般加常数的转移需要判断）（这里求最大值，ij越小值越小，所以可以先转移 $f[i-1][j]$ ，哪怕不是最优也不影响最终结果）

优化1：a[i] == b[j]下，b[j] > b[k] 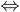$\Leftrightarrow$ a[i] > b[k]

此时，就可以维护一个 $g[i][j]$ ，借助之前的遍历j的结果来替代遍历k的结果

for (int i = 1; i <= n; ++ i) {g[i][0] = 1;for (int j = 1; j <= n; ++ j) {f[i][j] = f[i - 1][j];if (a[i] == b[j]) f[i][j] = max(f[i][j], g[i][j - 1]);g[i][j] = g[i][j - 1];if (a[i] > b[j]) g[i][j] = max(g[i][j], f[i - 1][j] + 1);}
}

$g[i][j] \Leftrightarrow max(f[i-1][k]) + 1 , k \in [1,j]$

这样的话，在 $a[i]$ 与 $b[j]$ 配对之后，想要尝试所有的转移只需要max一个 $g[i][j-1]$

之后，当前层更新 $g[i][j]$ ，留待下层配对之后需要尝试转移时使用

（转移与否还要看是否配对，我先维护好这个结构，同时这个结构的维护也需要考虑合法性，即严格递增：注意有些 $k$ 被 $a[i] > b[j]$ 过滤掉了）

优化2：注意到每个g[i][j]只会赋值一次，且运算只基于上一次的结果和无关项

#include <bits/stdc++.h>
using namespace std;
const int N = 3010;
int f[N][N], maxik;
int a[N], b[N];
int main()
{int n;cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n; i++) cin >> b[i];for(int i = 1; i <= n; i++){maxik = 1;for(int j = 1; j <= n; j++){f[i][j] = f[i-1][j];if(a[i] == b[j]) f[i][j] = max(f[i][j], maxik);if(a[i] > b[j]) maxik = max(maxik, f[i-1][j] + 1);}}int ans = 0;for (int i = 1; i <= n; ++ i) ans = max(f[n][i], ans);cout << ans << "\n";return 0;
}

这篇关于【最长公共上升子序列】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！