本文主要是介绍【pytorch06】 维度变换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
常用API
- view/reshape
- squeeze/unsqueeze
- transpose/t/permute
- expand/repeat
view和reshape
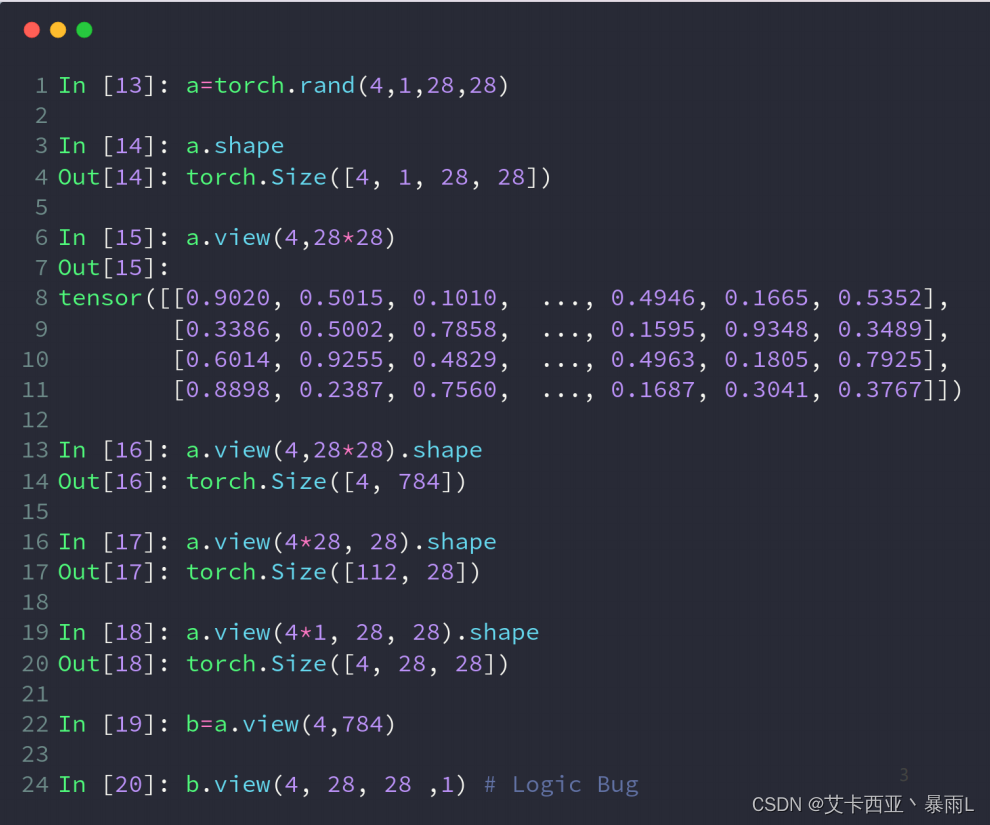
view操作的基本前提是保证numel()一致
a.view(4,28*28)的物理意义是把行宽以及通道合并在一起,对于4张图片,我们直接把所有数据都合在一起,用一个784维的向量来表示,这样所有的二维信息上下左右位置信息就忽略掉了,这种数据特别适合于全连接层,因为全连接层的输入就是这样的一个向量输入
a.view(4*28,28)把原来数据的前三个通道合并在一起,这种方式的物理意义是把所有的照片的所有通道的所有行放在第一个维度变成一个N,每一个N都有一个一行的数据,这一行的数据刚好是28个像素点[N,28],就是说我们现在只关注所有的行这些数据信息
a.view(4*1,28,28)把前面两个通道合并在一起,这种方式是说,我们只关注feature map这个属性,不关注feature map来自于哪张图片或哪个通道
view操作或reshape操作的致命问题
b是a通过view操作得到的,如果只看b不看a的话得到的是一个[4,784]的tensor,就会丢失非常重要的数据,原来的存储方式(维度信息)是[b,c,h,w],会丢失原来的维度信息,所以恢复的时候就恢复不出来,恢复的时候可以恢复成[4,28,28,1]这种方式从语法上来是没问题的,但是把数据破坏掉了,因为把维度信息丢失掉了,没有按照维度信息来还原数据就造成了数据的污染
数据的存储/维度顺序非常重要,需要时刻记住
如果view的新的tensor的size跟原来的不一样会报错原来是42828=4784,如果标成4783的话还有一部分数据不知道会去哪,没有把数据的size保持住
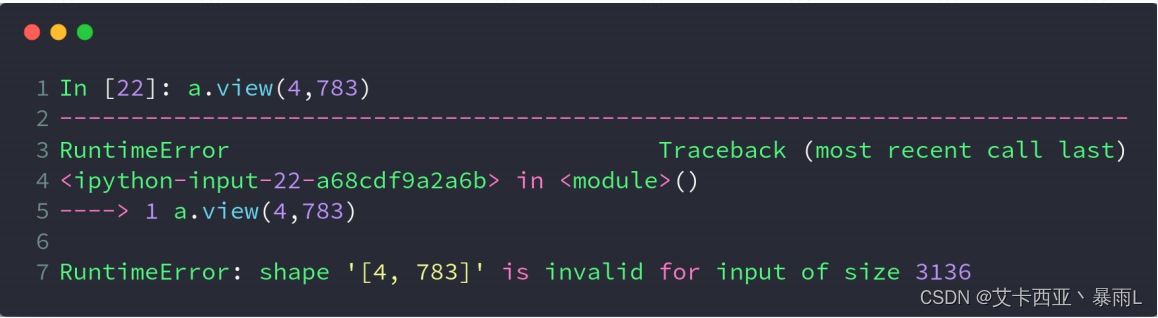
squeeze和unsqueeze
unsqueeze维度增加
unsqueeze把一个维度展开
范围在[-a.dim()-1,a.dim()+1] 这里是[-5,5)

a.unsqueeze(0).shape0维度前面插入一个维度,可以把这个维度理解为一个集合或者一个组,一个组里面有4个图片,每个图片有1个通道长宽为28
增加了一个组,但这个组还是4张图片,没有增加数据,只是数据的理解方式不一样
a.unsqueeze(-1).shape可以理解一个像素的均值和方差的属性,这里只是假设,便于理解,要理解的是unsqueeze并没有改变数据本身,只是改变数据的理解方式
负数是在索引之后插入,正数是在索引之前插入
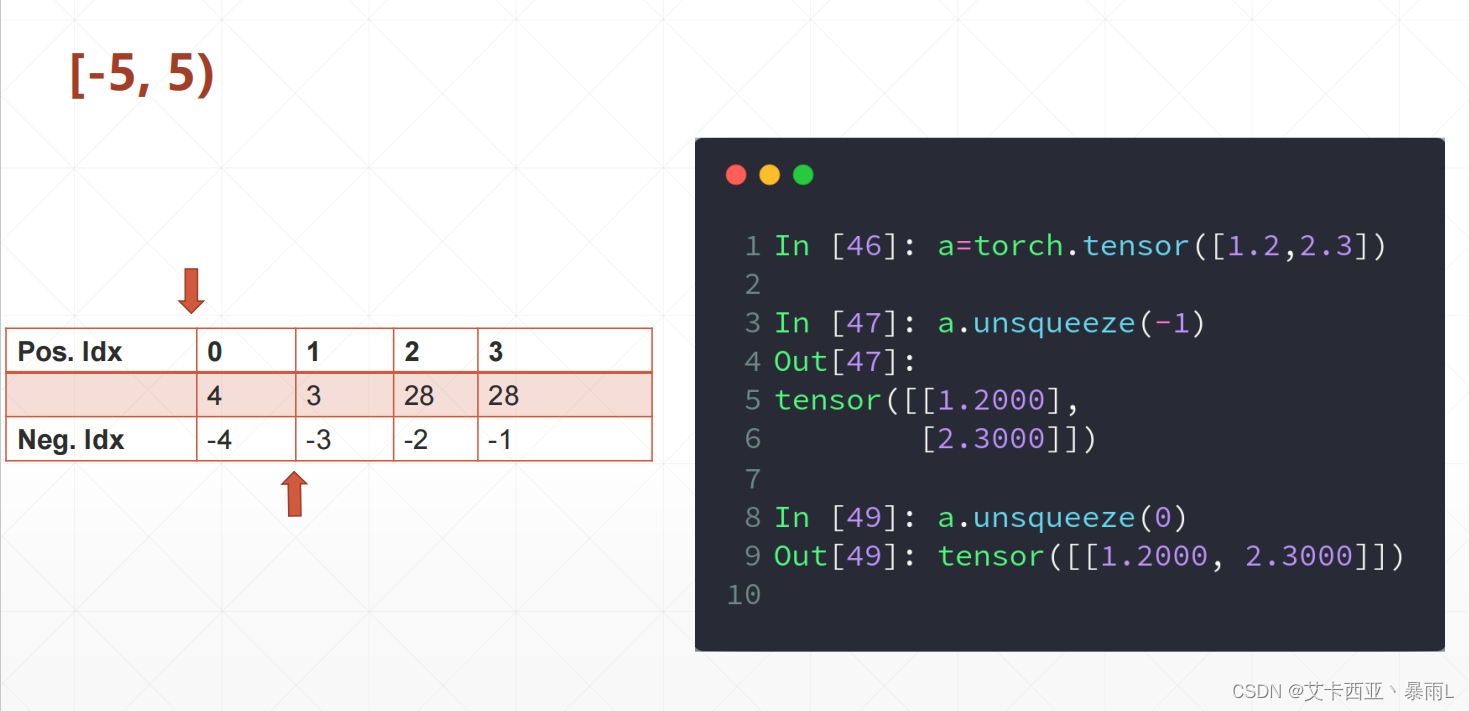
a的shape是[2],经过unsqueeze(-1)之后shape是[2,1],经过unsqueeze(0)之后shape是[1,2]
图片处理案例

feature map是[4,32,14,14]也就是给的照片长宽为14×14,channel为32,bias相当于给每个channel上的所有像素增加一个偏置值,如何把f叠加在b上?因为f和b的dimension不一样,所以shape也不一样,所以肯定要把b的dimension变成4维,保持与f的shape一样,才可以进行累加操作,然后再把它扩张成[4,32,14,14](扩张后面会说),这样就可以跟f相加了
squeeze维度减少

squeeze()能挤压的全部挤压,能挤压的包括dimension的size是1的
expand和repeat
- expand:boradcasting
- repeat:memory copied
维度扩展是把维度的shape改变掉
比如b[32]用unsqueeze操作把dimension为1的tensor变成了dimension为4的tensor[1,32,1,1],变成dimension为4的tensor以后fearture map还是[4,32,14,14]还是不能直接相加,我们需要把这1维度扩展成14维度

expand只是改变了我们的理解方式并没有增加数据
repeat实实在在的增加了数据,比如你把1变成4的时候增加了4张照片,因此他把后面的所有的数据都拷贝一遍,现在有1行要变成14行,那就会把14行的数据全部拷贝一遍
这两个api从最终的效果来说是等效的,第一种方式和第二种方式区别在于什么,第一种方式不会主动复制数据只会在有需要的时候才会复制数据否则就会省略掉复制数据这个过程(推荐)执行速度快节约内存

调用expand函数的前提是tensor原来的shape和expand之后的shape的dimension必须一致,对于原来1维度扩展以后是n维度的话是可以扩张的,对于原来维度不为1的维度不可行(比如原来是3 expand之后变成M的话这一部分操作没办法复制,必须告诉策略是什么,所以会报错)
如果不想改变某一维度只需要填上-1即可,-1表示这个维度保持不变

repeat的接口和expand不一致,它给的参数不是新的shape,而是每一个dimension要拷贝的次数
T转置
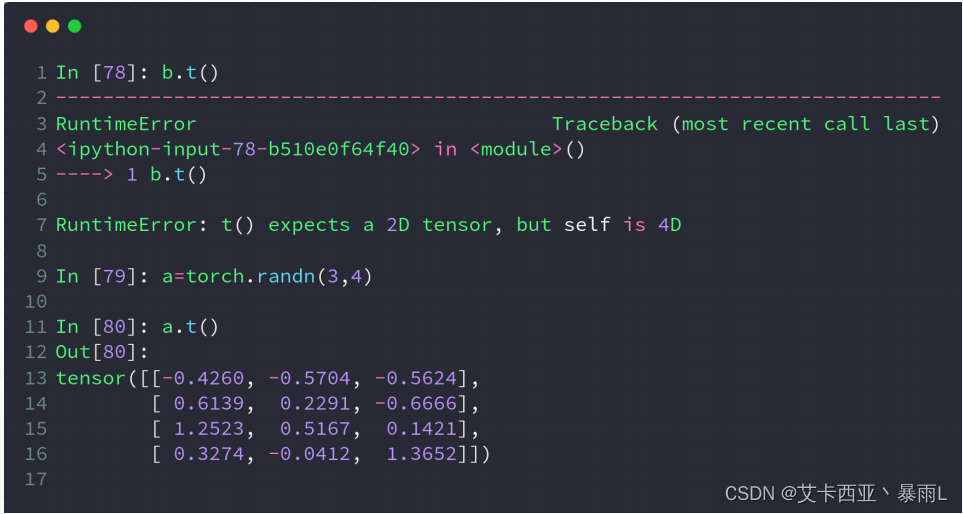
.t()方法只适用于2-D的tensor,只能适用于矩阵
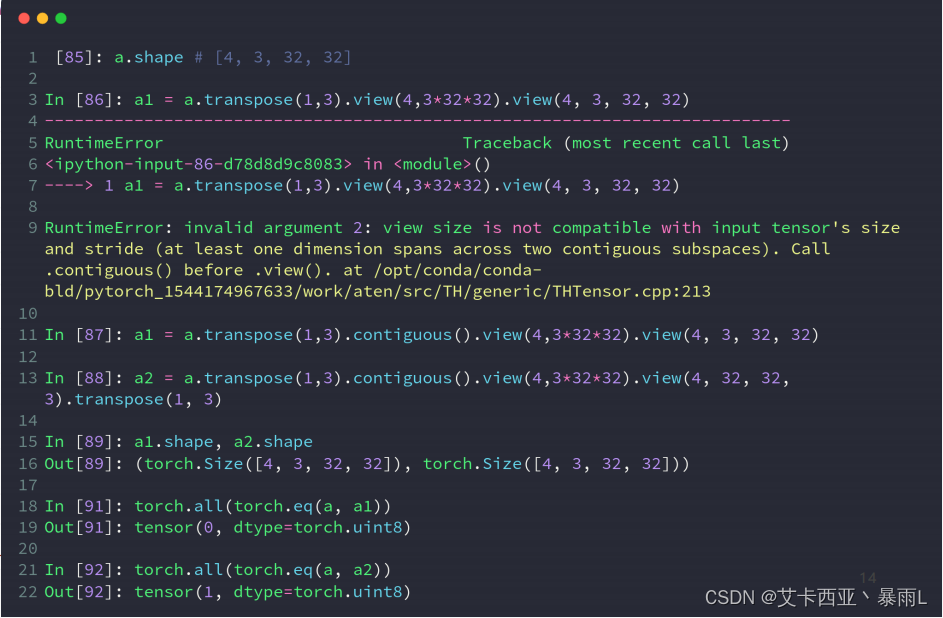
transpose接受的是两个参数包含了要交换的两个维度a.transpose(1,3)这里要交换1维度和3维度,本来是[b,c,h,w]会变成[b,w,h,c],然后把后面的3个维度连起来一起理解再把它展开成[4,3,32,32]就会变成[b,c,w,h],问题就来了
view操作会把维度信息给丢掉,没有考虑到原来的维度顺序是[b,w,h,c],展开的时候变成了[b,c,w,h]这样子c维度就会提前,通过这种方式破坏了原来的数据
数据的维度顺序必须和存储顺序保持一致
另一个问题是,transpose涉及到维度交换,因此原来的数据存储方式肯定是要改变的,本来说原来是一行行的存储,转置之后数据是不连续的。
在PyTorch中,当提到张量(tensor)是“不连续的”(non-contiguous),意思是张量的数据在内存中不是紧密排列的,而是分散在不同的位置。这通常发生在对张量进行某些操作后,比如切片(slicing)、索引(indexing)或者某些形式的拼接(catenation),这些操作可能导致张量的数据在内存中不再连续。
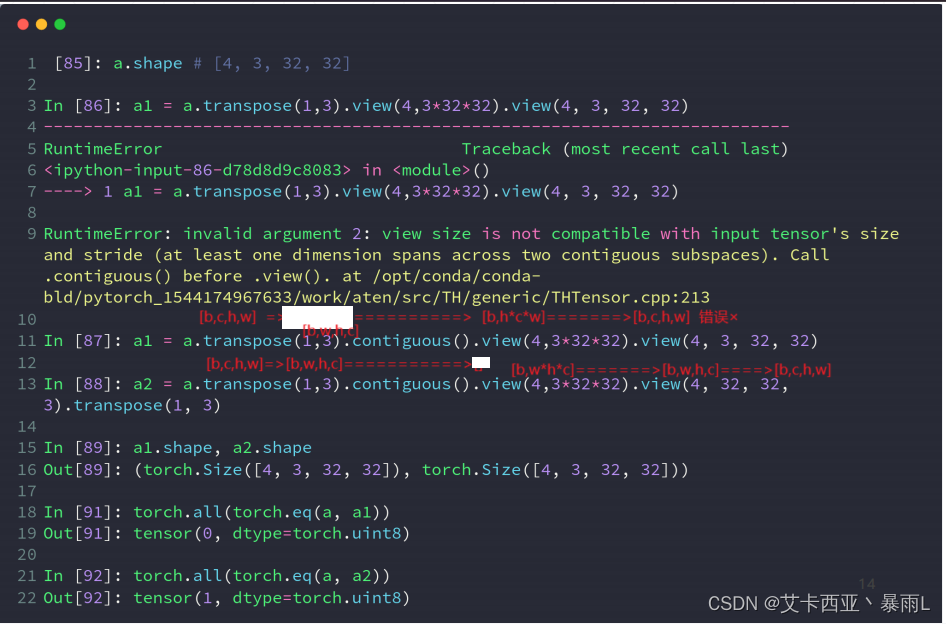
a2=a,a1≠a
torch.eq()来判断数据内容是否一致,再用torch.all()函数来确保所有内容都是一致的
torch.all()函数用于检查给定条件是否对输入张量(tensor)的所有元素都为真(true)。如果张量中的所有元素都满足条件,则返回True,否则返回False。
可以看出要把维度的先后顺序保持住,否则会污染数据
permute

一开始维度是[b,c,h,w]用transpose(1,3)只能两两交换会变成[b,w,h,c],会发现w和h维度交换了(原来w在h的后面,现在h在w的前面),比如原来是一个人,现在交换之后变成了一个转置(长变宽,宽变长),它这个图片可能会改变所以图片不会是一个人,为了很好的还原出来原来的图片,只完成C放到后面的这个操作还是希望得到[b,h,w,c]这样的一个形状
两步
b=a.transpose(1,3) [b,w,h,c]
c=b.transpose(1,2) [b,h,w,c]
[b,h,w,c]是numpy存储图片的格式,需要这一步才能导出numpy
permute()实现上述操作只需要一步,可以完成任意维度的交换
同样permute()也会把内存顺序打乱,因此如果要涉及到contagious这个错误的话,必须要额外加一个contagious()函数,把内存顺序变连续,也就是重新生成一片内存再复制过来
这篇关于【pytorch06】 维度变换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








