本文主要是介绍基于ACO蚁群优化的城市最佳出行路径规划matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
基于ACO蚁群优化的城市最佳出行路径规划matlab仿真,可以修改城市个数,输出路径规划结果和ACO收敛曲线。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
点数较少时
点数规模中等时


点数较多时


(完整程序运行后无水印)
3.核心程序
...............................................................................% 更新最短路径及其信息素[Vmin,Imin] = min(Rdist);Ant_min(t) = Vmin;Lrout(t,:) = Lrt(Imin,:);if Ant_min(t)<GminGmin = Ant_min(t);route(1,1:Ncity+1) = Lrout(t,:);end% 强化信息素更新for f=1:5[Rdist_min,Imin]=min(Rdist);for c=1:Ncitydtw2(Lrt(Imin,c),Lrt(Imin,c+1)) = dtw2(Lrt(Imin,c),Lrt(Imin,c+1))+e*(Q/Gmin);end Rdist(Imin)=1e4;end% 信息素更新for i=1:Ncityfor j=1:Ncitytaws(i,j) = (1-efact)*taws(i,j)+dtw1(i,j)+dtw2(i,j);endendtaws;% 绘制当前迭代的路径for i=1:Ncity+1x1(i) = x(Lrout(t,i));y1(i) = y(Lrout(t,i));end
end% 绘制全局最短路径跟踪图
figure
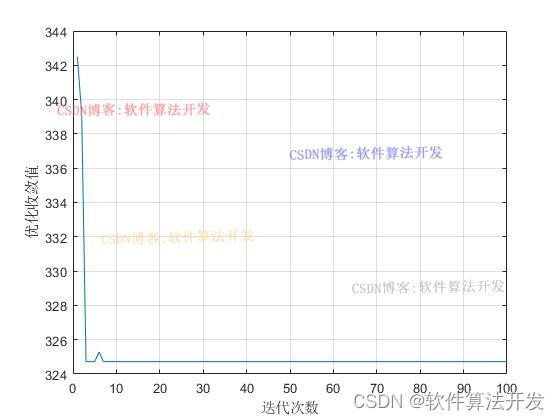
plot(1:t,Ant_min)
xlabel('迭代次数')
ylabel('优化收敛值')
grid on for i=1:Ncity+1x1(i)=x(route(1,i));y1(i)=y(route(1,i));
endfigure
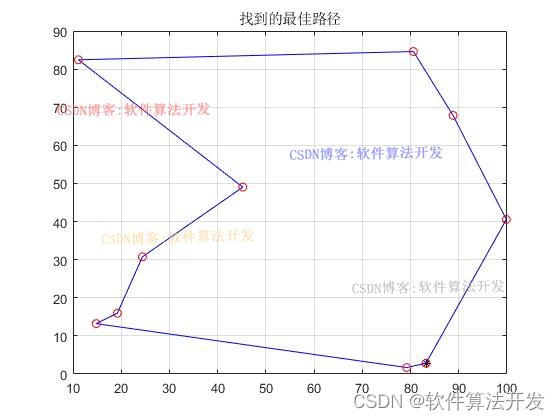
plot(x(1),y(1),'*k')
hold on
plot(x1,y1,'b')
hold on
plot(x,y,'ro')
title('找到的最佳路径')
grid on
624.本算法原理
蚁群优化算法(Ant Colony Optimization, ACO)是一种启发式优化方法,灵感来源于蚂蚁在寻找食物过程中留下信息素并据此选择最短路径的行为。将其应用于城市最佳出行路径规划问题时,能够模拟蚂蚁探索不同路径并逐渐发现较优路径的过程,从而找到从起点到终点的最佳出行路线。在城市路径规划的ACO框架中,主要元素包括:
- 城市节点:代表地图上的各个地点,如路口、地标等;
- 边:连接两节点之间的路径,附带旅行成本(如距离、时间或费用);
- 蚂蚁:模拟个体,每只蚂蚁从起点出发,按照一定规则探索路径至终点;
- 信息素:沿路径释放,其浓度影响后续蚂蚁的选择,随时间蒸发。
ACO算法步骤:

整个ACO算法的数学抽象可以总结为一个迭代优化过程,目标函数(最小化路径总长度)通过群体智能和信息素机制隐式求解。其中,信息素浓度的动态平衡体现了记忆与遗忘的自然法则,而启发式信息与信息素的联合决策机制,则巧妙地融合了全局探索与局部利用的策略,使得算法在复杂网络中具有较强的搜索能力和适应性。
5.完整程序
VVV
这篇关于基于ACO蚁群优化的城市最佳出行路径规划matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




