吴恩达机器学习第三课 week1 无监督学习算法（上）

本文主要是介绍吴恩达机器学习第三课 week1 无监督学习算法（上），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

01 学习目标

02 无监督学习

03 K-means聚类算法

3.1 K-means聚类算法原理

3.2 k-means算法实现

3.3 利用k-means算法压缩图片

04 总结

01 学习目标

（1）了解无监督学习算法

（2）掌握K-means聚类算法实现步骤

（3）利用K-means聚类算法压缩图片

02 无监督学习

概念：根据未被标记的训练样本解决模式识别或结构问题的算法，为无监督学习算法。

主要算法：

应用（摘自“文心一言”）：

（1）数据挖掘：

聚类分析：对大规模的客户数据进行聚类，发现不同特征的客户群体，为精细化营销和个性化推荐提供支持。
异常检测：无监督学习可以识别数据中的异常点，帮助企业发现潜在的风险因素。
关联规则挖掘：发现不同产品之间的关联性，为商品搭配和交叉销售提供依据。

（2）自然语言处理：

主题模型：从大规模文本数据中提取主题和话题，为舆情分析和信息检索提供支持。
情感分析：可以挖掘文本中的情感倾向和情绪色彩，为舆情监控和口碑管理提供参考。
文本聚类：可以对文本数据进行聚类分析，为信息检索和文本分类提供支持。

（3）社交网络分析（社区发现）通过聚类和网络分析揭示社交网络的组织结构和信息传播模式。

（4）推荐系统（用户行为分析）：可以分析用户的历史行为数据，发现用户的兴趣和行为模式，从而为用户提供个性化的推荐结果。

（5）自动驾驶（环境和道路感知）：无监督学习用于对传感器数据进行聚类和降维，提取出道路、车辆和行人等重要特征，以支持自动驾驶决策和控制。

（6）计算机视觉（图像分割）：可以对图像中的像素进行聚类，实现图像的自动分割，为对象识别、图像分析等进一步处理提供支持。（特征学习）：无监督学习能够从图像数据中学习更高层次的特征表示，提高图像识别和分类的准确性和鲁棒性。

（7）降维（数据处理）：无监督学习算法如主成分分析（PCA）和t-SNE等，用于降低数据的维度，减少数据中的冗余信息，提高数据的可视化、处理和分析效率。

（8）生成模型（数据生成）：无监督学习可以生成新的数据，例如，通过从一个概率分布中学习数据的分布特征，生成新的图像、文本或语音数据。

03 K-means聚类算法

下面，将采用jupyter notebook实现K-means算法，并将其用于图像压缩。

3.1 K-means聚类算法原理

算法步骤：

①，假设n个类的质心

②，计算各points（数据点）到质心的距离，并将points分配给最近的质心

$c^{(i)}:=j\; that\;minimizes\;||x^{(i)}-\mu _{j}||^2$

$c ^{(i)}:=j$ 表示第i个点距离第j个质心最近， $x ^{(i)}$ 是第i个点的坐标， $\mu _j$ 是第j个质心的坐标。上式会返回质心索引号列表。通俗地讲，给每个点贴个标签，标签上是距离其最近的质心编号，即：如果第1~3个点分别距离第2、0、1个质心最近，则返回列表[2 0 1]。

③，根据第②步分配结果重新计算质心

$\mu_k=\frac{1}{|C_k|}\sum x^{(i)}$

$\mu_k$ 为第k个质心的坐标， $C_k$ 为分配到第k个质心的点集合， $|C_k|$ 为该集合点的数量。上式会返回质心坐标的列表。通俗地讲，上式计算的结果为质心与所属点集合的平均距离，即：如果有10个点分配给了第1个质心， $\mu_1$ 就是这10个点到该质心的平均距离。

④，重复第②和③步，直至质心位置不再变化，聚类结束（如下图）

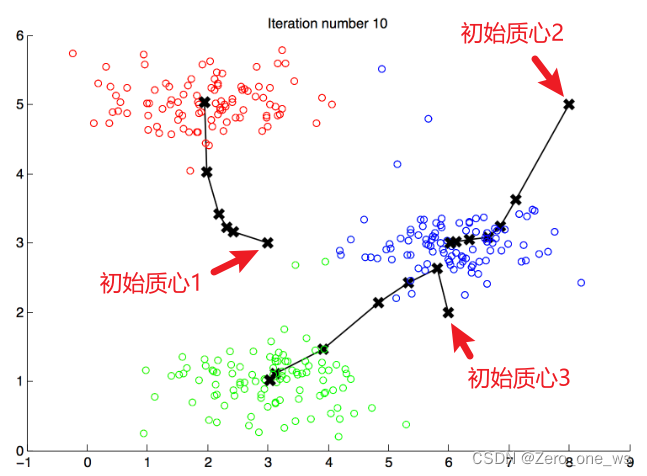
聚类的结果受初始质心的影响，因此，可以多次随机假设质心进行计算，最终取cost最小的计算结果。

3.2 k-means算法实现

（1）导入计算模块

import numpy as np
import matplotlib.pyplot as plt
from utils import *%matplotlib inline

（2）定义距离计算函数

def find_closest_centroids(X, centroids):# 质心索引idx = np.zeros(X.shape[0], dtype=int)for i in range(len(X)):distances = np.sum((X[i] - centroids) ** 2, axis=1)idx[i] = np.argmin(distances)return idx

（3）定义质心坐标计算函数

def compute_centroids(X, idx, K):m, n = X.shape# 质心坐标centroids = np.zeros((K, n))for k in range(K):points = X[idx == k]centroids[k] = np.mean(points, axis=0) return centroids

（4）定义k-means执行函数

def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):m, n = X.shapeK = initial_centroids.shape[0]centroids = initial_centroidsprevious_centroids = centroids    idx = np.zeros(m)# 开始执行K-Meansfor i in range(max_iters):# 过程输出print("K-Means iteration %d/%d" % (i, max_iters-1))# 分配pointsidx = find_closest_centroids(X, centroids)# 结果可视化if plot_progress:plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)previous_centroids = centroids  # 计算质心坐标centroids = compute_centroids(X, idx, K)plt.show() return centroids, idx

（5）开始聚类

X = load_data() # 加载数据initial_centroids = np.array([[3,3],[6,1],[8,5]]) # 设置初始质心坐标
K = 3          # 质心个数max_iters = 6  # 迭代次数centroids, idx = run_kMeans(X, initial_centroids, max_iters, plot_progress=True)

运行以上代码，结果如下：

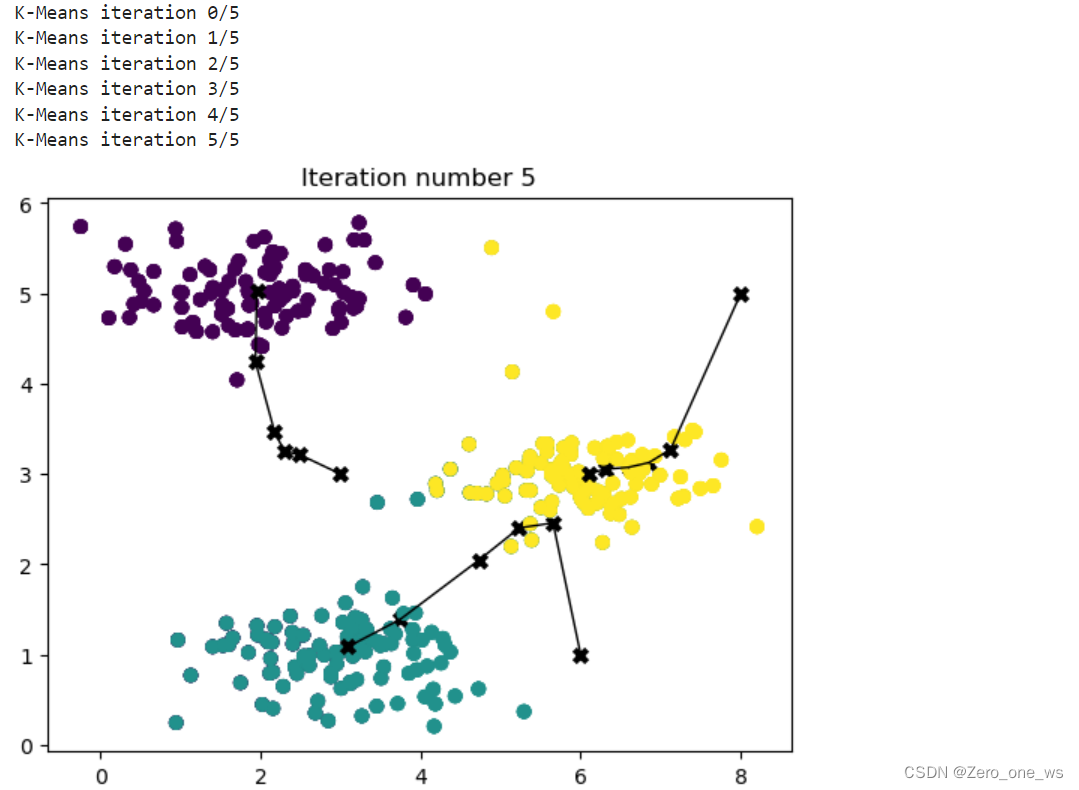
3.3 利用k-means算法压缩图片

从网上下载了1张色彩鲜明的图片，利用3.2节的函数，开始压缩吧！

（1）定义质心随机生成函数

def kMeans_init_centroids(X, K):# 随机重新排序索引randidx = np.random.permutation(X.shape[0])# 选择前K个样本作为质心centroids = X[randidx[:K]]return centroids

（randidx = np.random.permutation(X.shape[0])：使用NumP的 np.random.permutation 函数来随机重新排序 X 的行索引（即样本的索引）。这样做是为了在选择质心时，样本是随机选取的，而不是简单地按顺序选取。

centroids = X[randidx[:K]]：从随机重新排序的索引 randidx 中选择前 K 个索引，并使用这些索引从 X 中选择相应的样本作为初始质心。）

（2）读取图片，并打印图片信息

original_img = plt.imread('./images/pic.jpg')
plt.imshow(original_img)
print("Shape of original_img is:", original_img.shape)

运行以上代码，结果如下：

Shape of original_img is: (400, 600, 3)

（3）图片归一化

# matplotlib处理对象为int或float，故将像素归一化至范围0 - 1
original_img = original_img / 255# K-means处理对象为矩阵，故将图片转为 m x 3 矩阵，m=400*600=240,000
X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))

（4）图片压缩

# 执行 K-Means 算法
# 下面设置质心数和迭代数，可多次试算
K = 6                       
max_iters = 10               # 随机生成初始质心 
initial_centroids = kMeans_init_centroids(X_img, K) 
# 开始压缩
centroids, idx = run_kMeans(X_img, initial_centroids, max_iters) # 取图片具有代表性的前K个质心颜色，代替原图
X_recovered = centroids[idx, :] # 将图片转为三维
X_recovered = np.reshape(X_recovered, original_img.shape)

（5）图片可视化

fig, ax = plt.subplots(1,2, figsize=(8,8))
plt.axis('off')ax[0].imshow(original_img)
ax[0].set_title('Original')
ax[0].set_axis_off()ax[1].imshow(X_recovered)
ax[1].set_title('Compressed with %d colours'%K)
ax[1].set_axis_off()

运行以上代码，结果为：

压缩原理：

首先确定6个初始质心，利用k-means算法聚类到最能代表该图片的6类颜色，将所有像素点分配给这6个“质心”。最终，将采用这个6类颜色作为该图片的代表色。

小知识：RGB模式有3个颜色通道（red,green,blue），每个通道有2^8=256种颜色，因此，每个像素点需要24位（3*8 bit）。

原始图像尺寸为400*600，共240,000个像素点。压缩前原图总位数为400*600*24=5,760,000 bit；压缩后采用6种颜色的字典来存储额外的空间，每种颜色需要24位，所占空间为6*24=144 bit，图像的240,000个像素点每个点占位4 bit（颜色质心≤16时均采用4个占位，即2^4=16）。因此，最终使用的位数为16*24 + 400*600*4=960,144 bit，这意味着可以将原始图像压缩约6倍。