本文主要是介绍广度优先搜索与最短路径问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《算法图解》上看到的分析思路,把广度优先搜索直接与最短路径问题放在一起,mark一下
1、BFS解决最短路径问题
假设要从双子峰前往金门大桥。你想乘公交车前往,并希望换乘最少。可乘坐的公交车如下:
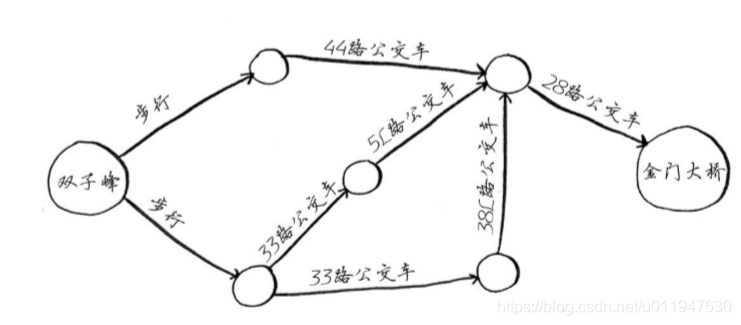
为找出换乘最少的乘车路线,你将使用什么样的算法? 一步就能到达金门大桥吗?下面突出了所有一步就能到达的地方:
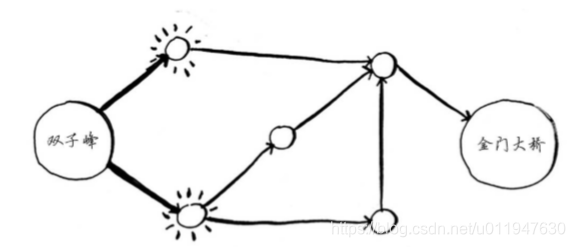
金门大桥未突出,因此一步无法到达那里。两步能吗?
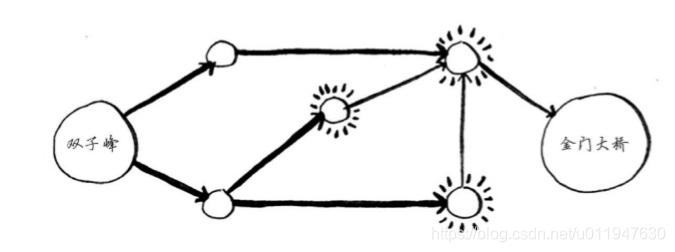
金门大桥也未突出,因此两步也到不了。三步呢?

2、BFS解决A到B路径是否存在的问题
与上述同样的分析思路,先找一步可达到的节点,再找二步、三步……
3、BFS与队列
队列的特点:先入先出
BFS的执行过程:是否存在A到B的路径
①申请队列,根节点A入队;
②若队列非空,节点出队,检查该节点是否是要搜索的目标节点B;若非B,则将出队节点的下一步节点入队;若是B,则终止;
③循环步骤2,直到队列为空,或找到目标节点B
4、运行时间
查找是否存在由A到B的路径,意味着将沿着每条路径搜索,因此运行时间至少是O(边数);此外,还使用了队列,包含了每个要检查的节点,将每个节点加入队列需要的时间是固定的,即O(1),因此总时间是O(节点数)。所以,广度优先搜索的运行时间是O(边数+节点数),通常写作O(V+E),V为顶点数vertice,E为边数edge。
这篇关于广度优先搜索与最短路径问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







