本文主要是介绍Keras入门教程 ——1.线性回归建模(快速入门),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Keras入门教程
- 1.线性回归建模(快速入门)
- 2.线性模型的优化
- 3.波士顿房价回归(MPL)
- 4.卷积神经网络(CNN)
- 5.使用LSTM RNN进行时间序列预测
- 6.Keras 预训练模型应用
线性回归建模(快速入门)
前言
Keras 是何物?Keras 是一个用 Python 编写的高级神经网络 API。其是以TesorFlow作为后端运行的。我们安装深度学习框架tensorflow时自动安装的,并非单独安装,作为tesorflow的API存在,使用起来非常方便。本文先用sklearn 线性回归模型,引入深入学习的keras进行建模。为了更好的快速入门深度学习的keras,仅从程序(代码)实现方面对深度学习有个感性的认识。看完这系列文章,你对机器学习中深度学习有一个更深的理解。
导入包
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
%matplotlib inline
%matplotlib inline的作用:在Jupyter Notebook中使用Matplotlib绘图时,如果不使用%matplotlib inline,图形将会在一个新的浏览器窗口中打开。这对于用户来说可能并不方便,因为这意味着每次执行绘图代码时都需要手动打开新窗口。使用%matplotlib inline可以将Matplotlib图形直接嵌入到Notebook单元格的输出中,这样用户就不需要手动打开新窗口了。
数据导入
以income数据集为例,由于数据比较小,所以直接写入代码。
data=pd.DataFrame(columns=['Education','Income'],data=[[10.00000,26.65884],
[10.40134,27.30644],
[10.84281,22.13241],
[11.24415,21.16984],
[11.64548,15.19263],
[12.08696,26.39895],
[12.48829,17.43531],
[12.88963,25.50789],
[13.29097,36.88459],
[13.73244,39.66611],
[14.13378,34.39628],
[14.53512,41.49799],
[14.97659,44.98157],
[15.37793,47.03960],
[15.77926,48.25258],
[16.22074,57.03425],
[16.62207,51.49092],
[17.02341,61.33662],
[17.46488,57.58199],
[17.86622,68.55371],
[18.26756,64.31093],
[18.70903,68.95901],
[19.11037,74.61464],
[19.51171,71.86720],
[19.91304,76.09814],
[20.35452,75.77522],
[20.75585,72.48606],
[21.15719,77.35502],
[21.59866,72.11879],
[22.00000,80.26057]])
# 可以查看data内容
data
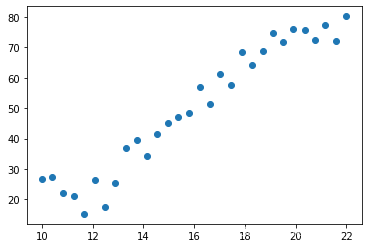
数据可视化
plt.scatter(data.Education,data.Income);
分离数据
X=data.Education.values.reshape(-1,1)
y=data.Income
Sklearn 建模
model_lr=LinearRegression()
model_lr.fit(X,y)
查看线性相关属性
print( "斜率:", model_lr.coef_[0] ," 截距:",model_lr.intercept_)
print("R^2=",model_lr.score(X,y))
MSE=mean_squared_error(y,y_pred)
print("MSE:",MSE)
斜率: 5.599483656931067 截距: -39.44626851089707
R^2= 0.9309626013230593
MSE: 29.828741902209323进行预测
y_pred=model_lr.predict(X)
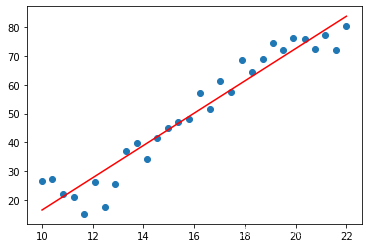
画回归曲线
plt.scatter(X,y)
plt.plot(X,y_pred,"r")
keras 建模
from keras.models import Sequential
from keras.layers import Densemodel_kr = Sequential()
model_kr.add(Dense(1,input_shape=(1,),activation='linear'))
查看模型
model_kr.summary()
Model: “sequential”Layer (type) Output Shape Param #
dense (Dense) (None, 1) 2=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0选择损失函数和优化方法
model_kr.compile(optimizer='adam' , loss='mse')
model_kr.fit(X , y , epochs=200 , verbose=1)
进行200次的结果如下
Output exceeds the size limit. Open the full output data in a text editor
Epoch 1/200
1/1 [==============================] - 0s 394ms/step - loss: 835.3273
Epoch 2/200
1/1 [==============================] - 0s 6ms/step - loss: 834.3919
Epoch 3/200
1/1 [==============================] - 0s 9ms/step - loss: 833.4571
Epoch 4/200
1/1 [==============================] - 0s 5ms/step - loss: 832.5229
Epoch 5/200
1/1 [==============================] - 0s 10ms/step - loss: 831.5893
Epoch 6/200
1/1 [==============================] - 0s 9ms/step - loss: 830.6564
Epoch 7/200
1/1 [==============================] - 0s 14ms/step - loss: 829.7242
Epoch 8/200
1/1 [==============================] - 0s 4ms/step - loss: 828.7927
Epoch 9/200
1/1 [==============================] - 0s 7ms/step - loss: 827.8617
Epoch 10/200
1/1 [==============================] - 0s 8ms/step - loss: 826.9315
Epoch 11/200
1/1 [==============================] - 0s 7ms/step - loss: 826.0019
Epoch 12/200
1/1 [==============================] - 0s 7ms/step - loss: 825.0732
Epoch 13/200
...
Epoch 199/200
1/1 [==============================] - 0s 6ms/step - loss: 666.1816
Epoch 200/200
1/1 [==============================] - 0s 9ms/step - loss: 665.4104
查看线性相关属性
W , b = model_kr.layers[0].get_weights()
print('线性回归的斜率和截距: %.2f, b: %.2f' % (W, b))线性回归的斜率和截距: 1.82, b: 0.19yks_pred=model_kr.predict(X)
MSE=model_kr.evaluate(y,yks_pred)
print("MSE1:",MSE)1/1 [==============================] - 0s 99ms/step - loss: 4833.7842
MSE1: 4833.7841796875惊奇的发现与上面做的结果相差很大
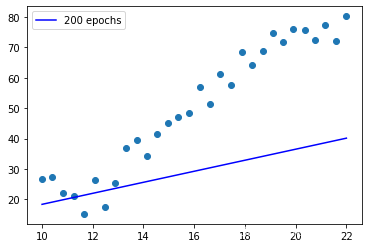
查看回归曲线
plt.scatter(X,y)
plt.plot(X,yks_pred,"b",label='200 epochs')
plt.legend()
画一下MSE曲线
plt.plot(history.epoch,history.history.get('loss'),label="loss")
plt.xlabel("epoch")
plt.ylabel("MSE")
plt.legend()

200 次远远没有达到理想结果
增加epoch次数
再多次运行fit结果如下:
再次提醒千万别把epoch调得很大。

结论
这个结果远没有原始线性回归好。
但是,有没有发现这里根本没有“深度”,只加了一层,根本没有发挥深度学习的优势。因此在实际的模型中,会加入多层(深度),进行建模。
下一篇,在此基础上,增加层和激活函数,优化此模型,进入下一篇。
这篇关于Keras入门教程 ——1.线性回归建模(快速入门)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




