本文主要是介绍Transformer预测 | 基于Transformer+LSTM股票价格预测时间序列预测(Pytorch),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
效果一览
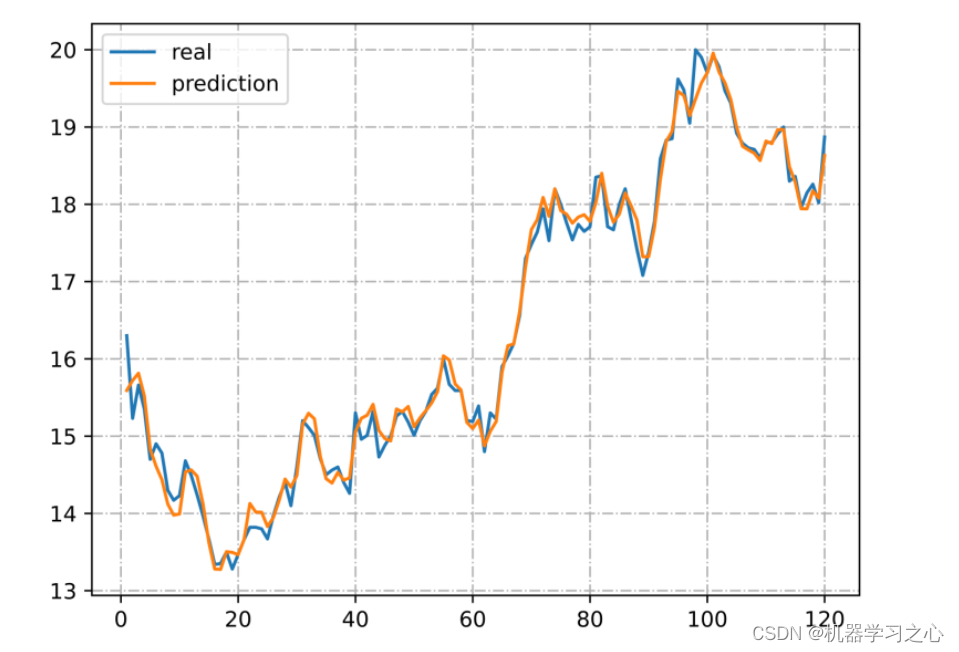
基本介绍
股票行情是引导交易市场变化的一大重要因素,若能够掌握股票行情的走势,则对于个人和企业的投资都有巨大的帮助。然而,股票走势会受到多方因素的影响,因此难以从影响因素入手定量地进行衡量。但如今,借助于机器学习,可以通过搭建网络,学习一定规模的股票数据,通过网络训练,获取一个能够较为准确地预测股票行情的模型,很大程度地帮助我们掌握股票的走势。本项目搭建了Transformer+LSTM成功地预测了股票的走势。
首先在数据集方面,我们选择上证000001号,中国平安股票(编号SZ_000001)数据集采用2016.01.01-2019.12.31股票数据,数据内容包括当天日期,开盘价,收盘价,最高价,最低价,交易量,换手率。数据集按照0.1比例分割产生测试集。训练过程以第T-99到T天数据作为训练输入,预测第T+1天该股票开盘价。(此处特别感谢Tushare提供的股票日数据集,欢迎大家多多支持)
在训练模型及结果方面,首先采用了LSTM(长短期记忆网络),它相比传统的神经网络能够保持上下文信息,更有利于股票预测模型基于原先的行情,预测未来的行情。LSTM网络帮助我们得到了很好的拟合结果,loss很快趋于0。之后,我们又采用比LSTM模型更新提出的Transformer Enc
这篇关于Transformer预测 | 基于Transformer+LSTM股票价格预测时间序列预测(Pytorch)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





