本文主要是介绍prim算法和kruskal算法详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在我们的数据结构中,当涉及到图的寻找最小的路径时,不得不提到最经典的寻找图的最小生成树的算法:
prim算法和kruskal算法详解。下面笔者将与大家共同探讨一下这两个经典的算法和他们的C++代码实现。
首先我们先看引自百度百科的prim算法的定义:普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。它的算法描述为:
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
下面开始通过一个例子来看看这个图的最小生成树的具体生成过程:
第一步:
初始的顶点集合V={A,B,C,D,E,F,G },Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
列出图的所有的边的信息:
边-----------权值
<A,D> --------5
<C,E> --------5
<D,F> --------6
<B,E> --------7
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
第二步:
以集合V任意一个顶点为Vnew新顶点集合中的第一个顶点元素,这里哦选顶点D为第一个:
Vnew ={D }
从V中除去顶点D
V={A,B,C,E,F,G }
可知.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一),与顶点D相通的有F,B,A ,E这四个顶点,在这个四个顶点中找到与顶点D距离最近的点,
<A,D> --------5
<D,F> --------6
<D,B> --------9
<D,E> --------15
由上可知是顶点A距离顶点D的权值为5最近,则可从中选出最短的一条边<A,D>放入Enew中,则Enew={<A,D>},再将顶点A加入Vnew集合中,则
Vnew={D,A}
从V中除去顶点A
V={B,C,E,F,G }
Enew={<A,D>}
得到图:
然后在顶点集合V={B,C,E,F,G }中再找到与 Vnew={D,A}中顶点最近的顶点
<D,F> --------6
<A,B> --------7
<D,B> --------9
<D,E> --------15
可知其中顶点F距离顶点D权值最小,距离最近,那么就将<D,F> --------6加入集合Enew中得到
Enew={<A,D>,<D,F>}
得到图:
、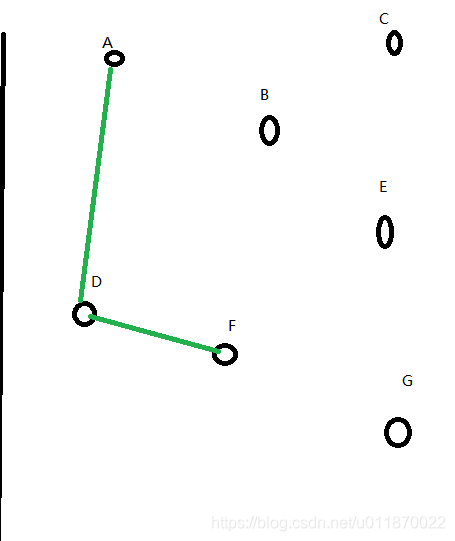
再将顶点F加入Vnew中,得到
Vnew={D,A,F}
从V中除去顶点F
V={B,C,E,G }
然后在顶点集合V={B,C,E,G }中再找到与 Vnew={D,A,F}中顶点最近的顶点
<A,B> --------7
<E,F> --------8
<D,B> --------9
<F,G> --------11
<D,E> --------15
可知其中顶点B距离顶点A权值最小为6,距离最近,那么就将<A,B>加入集合Enew中得到
Enew={<A,D>,<D,F>,<A,B>}
得到图:

再将顶点B加入Vnew中,得到
Vnew={D,A,F,B}
从V中除去顶点B
V={C,E,G }
然后在顶点集合V={C,E,G }中再找到与 Vnew={D,A,F,B}中顶点最近的顶点
<B,E> --------7
<B,C> --------8
<E,F> --------8
<F,G> --------11
<D,E> --------15
可知其中顶点E距离顶点B权值最小为7,距离最近,那么就将<B,E>加入集合Enew中得到
Enew={<A,D>,<D,F>,<A,B>,<B,E>}
再将顶点E加入Vnew中,得到
Vnew={D,A,F,B,E}
得到图:
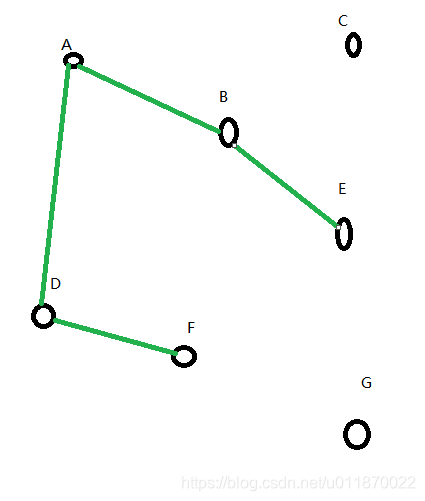
从V中除去顶点F
V={C,G }
然后在顶点集合V={C,G }中再找到与 Vnew={D,A,F,B,E}中顶点最近的顶点
<C,E> --------5
<B,C> --------8
<E,G> --------9
<F,G> --------11
可知其中顶点C距离顶点E权值最小为5,距离最近,那么就将<C,E>加入集合Enew中得到
Enew={<A,D>,<D,F>,<A,B>,<B,E>,<C,E>}
得到图:

再将顶点C加入Vnew中,得到
Vnew={D,A,F,B,E,C}
从V中除去顶点C
V={G }
最后从集合V={G }中再找到与 Vnew={D,A,F,B,E,C}中顶点最近的顶点
<E,G> --------9
<F,G> --------11
可知其中顶点G距离顶点E权值最小为9,距离最近,那么就将<E,G>加入集合Enew中得到
Enew={<A,D>,<D,F>,<A,B>,<B,E>,<C,E>,<E,G>}
得到图:

再将顶点G加入Vnew中,得到
Vnew={D,A,F,B,E,C,G}
从V中除去顶点G
V={}至此,所有的顶点都访问完毕,得到prim算法的最小生成图,其所有边为
<A,D>,<D,F>,<A,B>,<B,E>,<C,E>,<E,G>,节点的访问顺序为:
D–>A–>F–>B–>E–>C–>G
在此例中,最小生成树的权值之和为5+6+7+7+5+9 = 39。
下面我们又来看看kruskal算法的基本思路:
首先看kruskal算法的百度百科提供的基本思路:
先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E 中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
算法实现的基本步骤:
第一步:新建图G,G中拥有原图中相同的节点,但没有边;
第二步:将原图中所有的边按权值从小到大排序;
第三步:从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中;
第四步:重复第三步,直至图G中所有的节点都在同一个连通分量中。
下面我们依旧是以上面的例子来进行对该算法的图解:

第一步:
构造包含所有节点的空图G:

第二步:
对所有的边进行从小到大的 排列:
<A,D> --------5
<C,E> --------5
<D,F> --------6
<B,E> --------7
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
第三步:从所有边中选出权值最小的边加入图中,可知最小为<A,D>,<C,E>这两条边,这两条边都可以作为我们加入构造的空图中的第一条边,在这里选择 <A,D>这条边即可,得到新的图:

则剩下的边为:
<C,E> --------5
<D,F> --------6
<B,E> --------7
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的边<C,E>,该边满足:这条边连接的两个节点于图G中不在同一个连通分量中,那么我们就可以将该边加入新的图得到:

则剩下的边为:
<D,F> --------6
<B,E> --------7
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的边<D,F>,该边满足:这条边连接的两个节点于图G中不在同一个连通分量中,那么我们就可以将该边加入新的图得到:
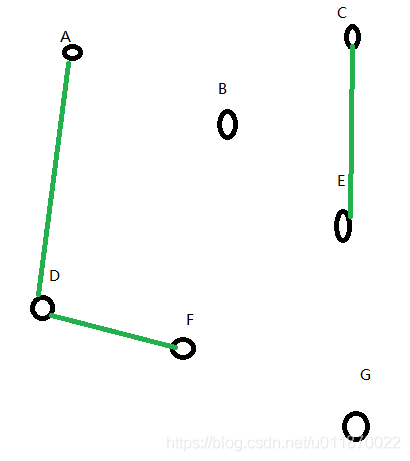
则剩下的边为:
<B,E> --------7
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的边<B,E>,<A,B>这两条边都满足:这条边连接的两个节点于图G中不在同一个连通分量中,那么我们就可以选择将其中一条边加入新的图得到,这里选择将<B,E> 加入新的图得到:

则剩下的边为:
<A,B> --------7
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的<A,B>,该边满足:这条边连接的两个节点于图G中不在同一个连通分量中, 加入新的图得到:

则剩下的边为:
<B,C> --------8
<E,F> --------8
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的边<B,C>,<E,F> 由于这两条边的两个顶点都在同一个连通分量上,所以这两条边都不满足:这条边连接的两个节点于图G中不在同一个连通分量中,不能加入到图G中,继续下一步 :
则剩下的边为:
<D,B> --------9
<E,G> --------9
<F,G> --------11
<D,E> --------15
在从中选出最小的边<D,B>,<E,G> ,其中<D,B>两个顶点都在同一个连通分量上,不满足条件,<E,G>则满足:这条边连接的两个节点于图G中不在同一个连通分量中,所以将<E,G>加入新的图得到:

则剩下的边为:
<D,B> --------9
<F,G> --------11
<D,E> --------15
经过查看,发现这些边均是两个顶点都在同一个连通分量中,所以均不符合加入到新图的条件,到此,一个完整的图的最小生成树就得到了。最终的图解为:

到此,prim算法和kruskal算法详解的讲解已经完成,剩下就是代码的实现了。至于代码实现的讲解,将在下一个博客文章中讲解。
这篇关于prim算法和kruskal算法详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





