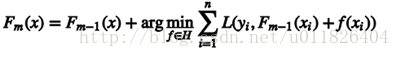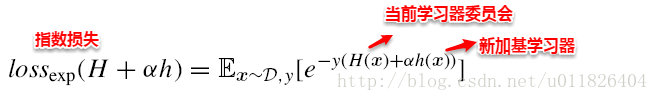本文主要是介绍GBDTGBRT与XGBoost,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在看清华学霸版《Python大战机器学习》的过程中,集成学习章节中出现了两个新的名词:GBDT&GBRT,也许是西瓜书定位于全面,而没有拘泥于细节。后来科普发现,这两个东西和陈天奇大神的XGBoost紧密相连,于是估摸着花时间弄懂这两个东西。
首先回顾一下集成学习的核心要点:在基学习器有一定准确性的基础上保证基学习器之间的多样性,总而言之即“好而不同”四字真言。集成学习主要有两种类型的学习算法:boosting串行,bagging并行。本篇主要围绕的是以决策树为基学习器的boosting方法。
前向分步算法
前面已经接触到了AdaBoost方法,其中主要包含两个步骤:(1)计算新引入的基学习器权重,(2)更新样本权重。之前只是简单提到:这两个公式是通过最优化指数损失函数而得到,事实上这里使用的正是前向分步算法,即每一步通过当前损失最优求解新基学习器参数。
很容易看出:Adaboost算法是前向分步算法的一个特例,使用指数损失最小化来求解新引入学习器的参数(即训练样本权重)及权重系数。
基于平方损失的提升树算法
提升树(boosting tree)是以决策树为基学习器的boosting方法,其预测性能相当优异。提升树迭代多棵回归树来共同决策,当采用平方误差损失函数时,损失函数刚好表达的是当前模型的拟合残差,使用前向分布算法,只需简单使用当前残差拟合得到一个回归树。
GBDT&GBRT
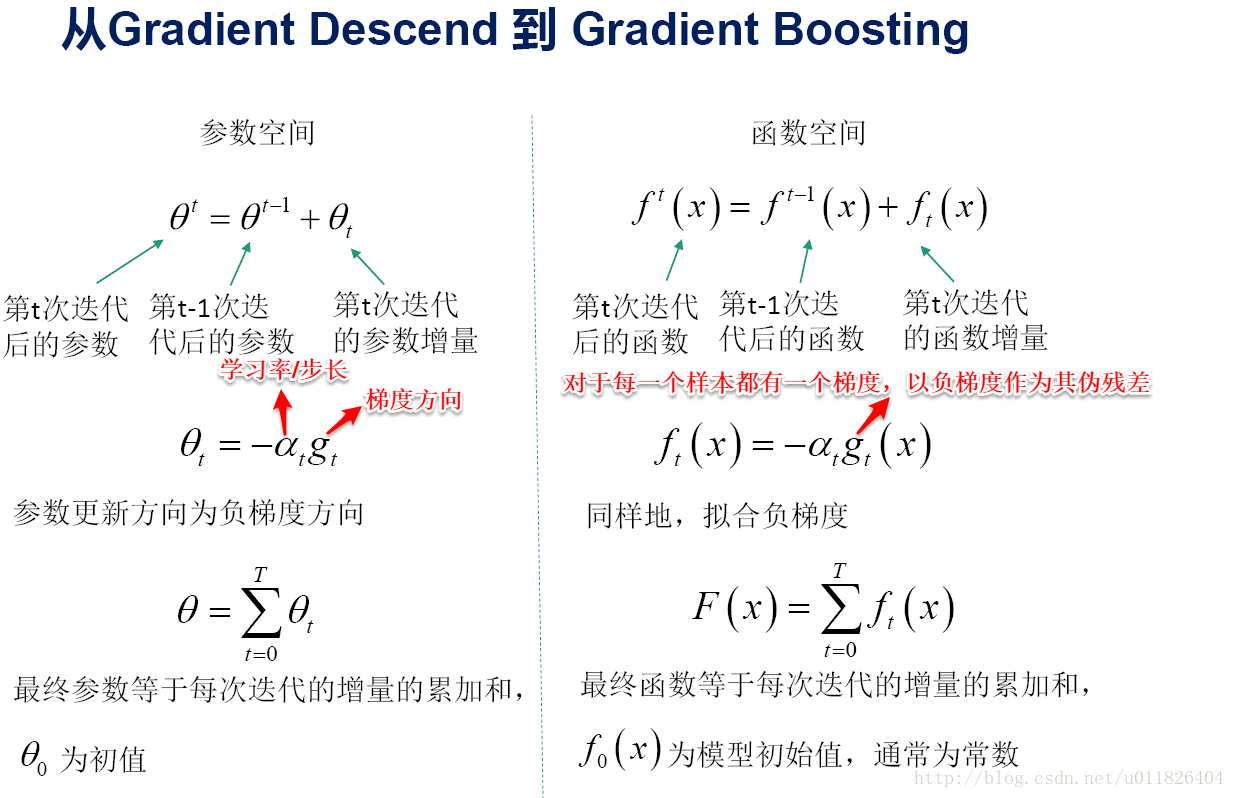
当损失函数是平方损失和指数损失时,使用前向分步算法求解十分容易;但对于一般函数时,最优化往往十分困难。 针对这一问题,Freidman提出了梯度提升算法:利用最速下降的近似方法,即利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值(伪残差),拟合一个回归树。在回归问题中,这称为梯度提升回归树(GBRT),分类问题则称为梯度提升决策树(GBDT)。
同时也可以使用梯度下降的思想来理解这一过程:若将当前模型的输出值看作一个变量,要使得损失函数最小化,实际上正是一个一维搜索问题,从当前模型的输出值出发,以负梯度方向来搜索最优值。对于新引入决策树划分的每个区域,分别计算其搜索步长,将新决策树在每个区域的预测值与搜索步长合并在一起,便等效于上面的每个区域重新计算输出值。
XGBoost
XGBoost全名为:eXtreme Gradient Boosting,在数据竞赛中风靡一时/披荆斩棘,它源于梯度提升框架,但是更加高效,秘诀就在算法能并行计算、近似建树、对稀疏数据的有效处理以及内存使用优化,这使得XGBoost至少比现有梯度提升算法有10倍的速度提升。下面是知乎上关于GBDT与XGBoost不同点的精彩回答,等有空拜读完论文再来谈谈自己的理解。
传统GBDT以CART作为基分类器,xgboost还支持线性分类器,这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归(分类问题)或者线性回归(回归问题)。
传统GBDT在优化时只用到一阶导数信息,xgboost则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。顺便提一下,xgboost工具支持自定义代价函数,只要函数可一阶和二阶求导。
xgboost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
Shrinkage(缩减),相当于学习速率(xgboost中的eta)。xgboost在进行完一次迭代后,会将叶子节点的权重乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。实际应用中,一般把eta设置得小一点,然后迭代次数设置得大一点。(补充:传统GBDT的实现也有学习速率)
列抽样(column subsampling)。xgboost借鉴了随机森林的做法,支持列抽样,不仅能降低过拟合,还能减少计算,这也是xgboost异于传统gbdt的一个特性。
对缺失值的处理。对于特征的值有缺失的样本,xgboost可以自动学习出它的分裂方向。
xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的?注意xgboost的并行不是tree粒度的并行,xgboost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。xgboost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),xgboost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
可并行的近似直方图算法。树节点在进行分裂时,我们需要计算每个特征的每个分割点对应的增益,即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以xgboost还提出了一种可并行的近似直方图算法,用于高效地生成候选的分割点。
这篇关于GBDTGBRT与XGBoost的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!