从零开始学数据结构系列之第三章《先序线索二叉树理论及线索化》

本文主要是介绍从零开始学数据结构系列之第三章《先序线索二叉树理论及线索化》，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

线索化

我们将对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化 。

现将某结点的空指针域指向该结点的前驱后继，定义规则如下：

若结点的左子树为空，则该结点的左孩子指针指向其前驱结点
若结点的右子树为空，则该结点的右孩子指针指向其后继结点这种指向前驱和后继的指针称为线索，将一棵普通的二叉树以某种次序遍历，并添加线索的过程称为线索化

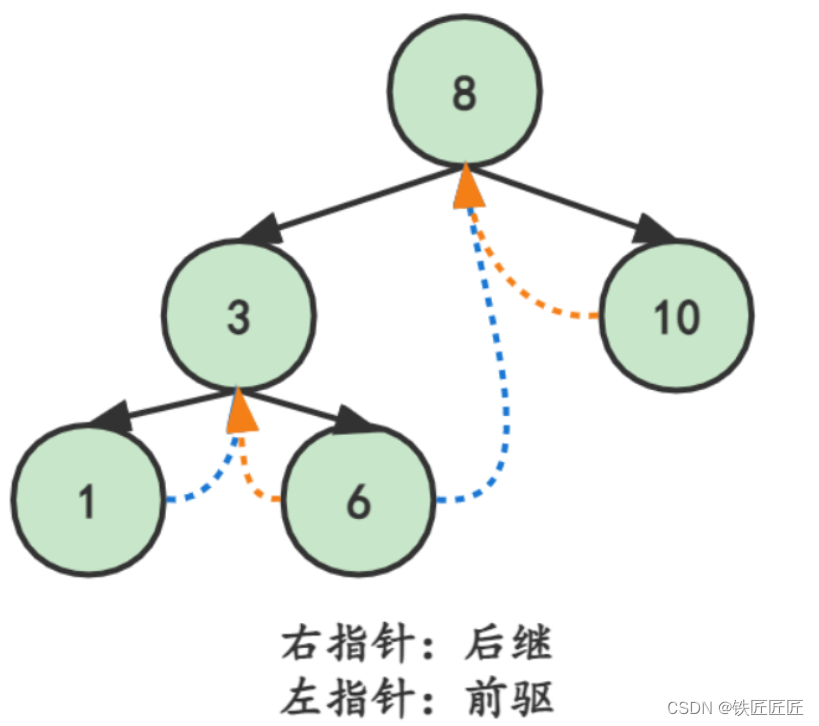
线索化带来的问题与解决

此时新的问题又产生了：我们如何区分一个lchild指针是指向左孩子还是前驱结点呢？

为了解决这个问题，我们需要添加标志位ltag和rtag,并定义以下规则

ltag==0，指向左孩子；ltag==1，指向前驱结点
rtag==0，指向右孩子；rtag==1，指向后继结点

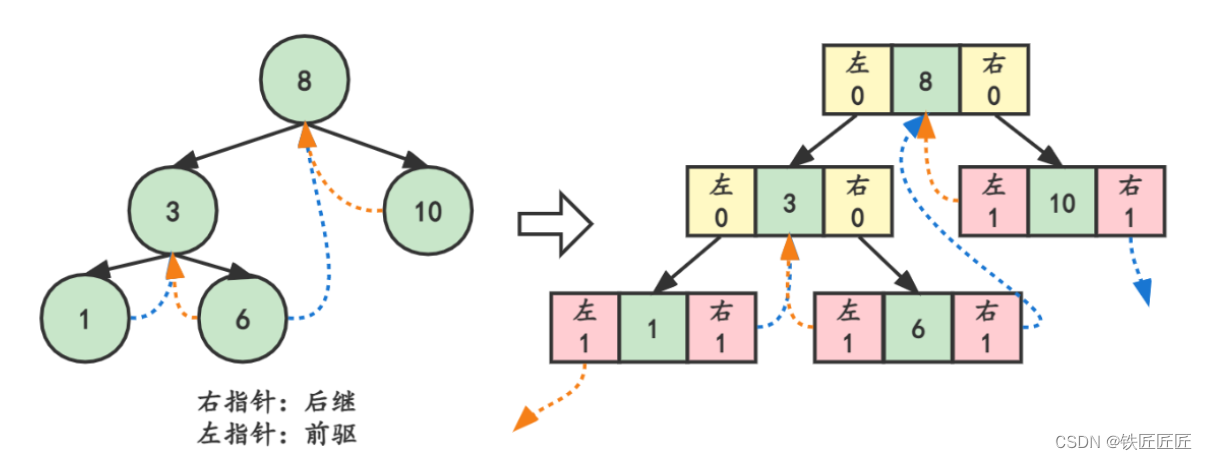
  线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继的信息只有在遍历该二叉树的时候才能得到，所以线索化的过程就是在遍历的过程中修改空指针的过程。

我们会中序线索二叉树的话，基本也会后续两个二叉树的，原理其实差不多的
就例如创树和结构初始化都是一样的

结构初始化

typedef struct TreeNode 
{char data;struct TreeNode *lchild;struct TreeNode *rchild;int ltag;int rtag;}TreeNode;

这边对比之前中序二叉树就多出这两个东西

ltag==0，指向左孩子；ltag==1，指向前驱结点
rtag==0，指向右孩子；rtag==1，指向后继结点

创树

void createTree(TreeNode** T,char* temp,int* index)
{char ch;ch = temp[*index];(*index)++;if( ch == '#') *T = NULL;else{*T =(TreeNode*)malloc(sizeof(TreeNode));(*T)->data = ch;(*T)->ltag = 0;(*T)->rtag = 0;createTree(&(*T)->lchild,temp,index);createTree(&(*T)->rchild,temp,index);		}
}

先序线索化

我们还是拿这张图

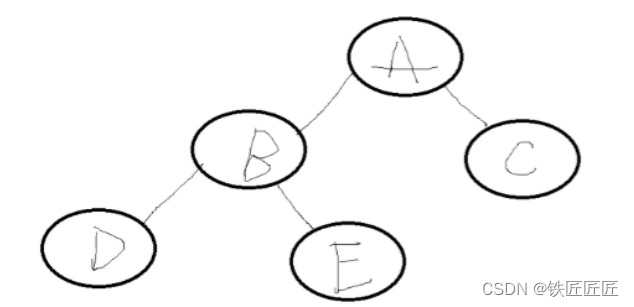
那么中序二叉树的排序则是

我们发现，那他与中序线索二叉树的区别只是从“左中右”更改成“中左右而已”

那我们先看之前我们中序线索二叉树是怎么成的

void inThreadTree(TreeNode* T, TreeNode** pre) 
{if(T){inThreadTree(T->lchild,pre);if(T->lchild == NULL){T->ltag = 1;T->lchild = *pre;}if(*pre != NULL && (*pre)->rchild == NULL){(*pre)->rtag = 1;(*pre)->rchild = T;}*pre = T;inThreadTree(T -> rchild, pre);}
}

那我们先序线索二叉树直接这样子不就行了

void inThreadTree(TreeNode* T, TreeNode** pre) 
{if(T){		if(T->lchild == NULL){T->ltag = 1;T->lchild = *pre;}if(*pre != NULL && (*pre)->rchild == NULL){(*pre)->rtag = 1;(*pre)->rchild = T;}*pre = T;inThreadTree(T->lchild,pre);inThreadTree(T -> rchild, pre);}
}

。

。

。

但是我们我们可以注意到，这样的排序是有问题的，我们仔细思索一下问题出现在哪里

由于我们是先遍历根，然后再去找他左右子树

把思维放宽些，假设我们遍历到节点“D”的时候

*此时的 pre = B 节点的，由于我们的D没有左子树，于是根据下面这个

if(T->lchild == NULL)
{T->ltag = 1;T->lchild = *pre;
}

则B变成D的左子树了

  后面判断后继节点时由于不满足条件，则跳过，再将*pre 赋值为D节点，于是我们继续向下执行

inThreadTree(T->lchild,pre);

​   看出问题没有，由于我们上面的D节点的左孩子已经赋值了，他后面再根据这个进行跳转回B节点，这样子的话就会无限递归了，那这样子我们要怎么解决呢？

​   我们看图知道，我们执行到D节点的时候，应该是不该继续执行inThreadTree(T->lchild,pre)这一段的，执行到B的时候是应该执行的，那么这两者的区别是啥?

B -----> ltag = 0
D -----> ltag = 1

​   于是，我们则可以根据我们之前给他设计的标签来进行判断，我们的inThreadTree(T->lchild,pre)这一段函数应不应该继续执行

最后我们可以得出这个

void inThreadTree(TreeNode* T, TreeNode** pre) 
{if(T){		if(T->lchild == NULL){T->ltag = 1;T->lchild = *pre;}if(*pre != NULL && (*pre)->rchild == NULL){(*pre)->rtag = 1;(*pre)->rchild = T;}*pre = T;if(T->ltag == 0)inThreadTree(T->lchild,pre);inThreadTree(T -> rchild, pre);}
}

往期回顾

1.【第一章】《线性表与顺序表》
2.【第一章】《单链表》
3.【第一章】《单链表的介绍》
4.【第一章】《单链表的基本操作》
5.【第一章】《单链表循环》
6.【第一章】《双链表》
7.【第一章】《双链表循环》
8.【第二章】《栈》
9.【第二章】《队》
10.【第二章】《字符串暴力匹配》
11.【第二章】《字符串kmp匹配》
12.【第三章】《树的基础概念》
13.【第三章】《二叉树的存储结构》
14.【第三章】《二叉树链式结构及实现1》
15.【第三章】《二叉树链式结构及实现2》
16.【第三章】《二叉树链式结构及实现3》
17.【第三章】《二叉树链式结构及实现4》
18.【第三章】《二叉树链式结构及实现5》
19.【第三章】《中序线索二叉树理论部分》
20.【第三章】《中序线索二叉树代码初始化及创树》
21.【第三章】《中序线索二叉树线索化及总代码》

这篇关于从零开始学数据结构系列之第三章《先序线索二叉树理论及线索化》的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---