本文主要是介绍单调栈(续)、由斐波那契数列讲述矩阵快速降幂技巧,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在这里先接上一篇文章单调栈,这里还有单调栈的一道题
题目一(单调栈续)
给定一个数组arr, 返回所有子数组最小值的累加和
就是一个数组,有很多的子数组,每个数组肯定有一个最小值,要把所有子数组的最小值的累加和。例如数组 [3 1 4 2] 子数组 3 的最小值是 3 子数组 3 1 的最小值是 1 子数组 3 1 4 的累加和是1 等等,把所有的累加和相加,就是我们要求的。这一题我们暴力解肯定是不行的,因为时间复杂度太高了 ...... 我们假设 i 位置的数是 x我们要找到以x 为最小值的子数组的范围,举个具体的例子, i =10位置的数是 7 ,我左边找离我最近的比我小的 值是 5 ,它在 5位置,右边离我最近的比我小的是 4 在 15 位置,中间这个位置是从哪到哪呢,是从 6 位置开始 到 14 位置结束,而且从 6 到 14 位置最小值是 这个7,我们看从6 到 14 这些数组中,有多少个是以7为最小值的,我们第一反应是都是,都是吗,我们假设 6位置是个10 我们 6 到 6位置就是以10 为最小值的,假设7位置是 8 那么 6 到 7 就是以 7位置的8 为最小值的,那到底有多少是以 10 位置的7 为最小值的呢,你只要跨过10位置的7,就都是以该位置为最小值的,比如 6到 10位置, 7到 10位置,10位置到11位置,等等,都是。 6 7 8 9 10 11 12 13 14 一共有多少个子数组呢,我们需要跨过 10 位置 6 7 8 9 10 5个数字 10 11 12 13 14 5个数字,所以一共有 5 * 5 = 25 个 。 我们推广一下,假如说 一个i 位置,它的值为 x ,左边离他最近的比它小的位置是k位置 值是 y,右边离他最近的比它小的位置是 j 值是z,那么产生多少累加和,i 是到不了k 的,得从 k + 1 开始,那有多少个开始位置呢 i - (k + 1) + 1个位置, 一化简,i - k 个位置,有多少个结束位置呢 (j - i )个结束位置,他们想 乘,就是子数组的数量这一题我们先假设是无重复值的。看是不是相当的清晰,注意刚刚我说是先假设无重复值的,那有点人就说,那我就是有重复值咋办,有重复值,就麻烦了,如果有重复值,我们需要做一些改进 举个栗子 2 4 5 3 6 6 6 3 7 8 6 3 5 3 2 ,我们关注 3 我们 3位置的 3 左边正常找比它小的,右边到 7 位置的 3 时我们就停住,在算 7 位置的 3时,左边比他小的位置可以算到 0位置的2 但右边就只能算到11位置的3 前一个位置。
代码如下:
public static int sumSubarrayMins(int[] arr){int[] left = nearLeftEqualsLeft(arr);int[] right = nearRightEqualsRight(arr);long sum = 0;for (int i = 0; i < arr.length; i++) {long start = i - left[i];long end = right[i] - i;sum += arr[i] * start * end;sum %= 1000000007;}return (int)sum;}private static int[] nearLeftEqualsLeft(int[] arr) {int[] result = new int[arr.length];Stack<Integer> stack = new Stack<>();for (int i = 0; i < arr.length; i++) {while (!stack.isEmpty() && arr[i] <= arr[stack.peek()]){Integer pop = stack.pop();result[pop] = stack.isEmpty() ? -1 : stack.peek();}stack.push(i);}while (!stack.isEmpty()){Integer pop = stack.pop();result[pop] = stack.isEmpty() ? -1 : stack.peek();}return result;}private static int[] nearRightEqualsRight(int[] arr){int[] result = new int[arr.length];Stack<Integer> stack = new Stack<>();for (int i = 0; i < arr.length; i++) {while (!stack.isEmpty() && arr[i] <= arr[stack.peek()] ){Integer pop = stack.pop();result[pop] = i;}stack.push(i);}while (!stack.isEmpty()){Integer pop = stack.pop();result[pop] = arr.length;}return result;}这里面用的是栈,时间复杂度为O(n),对于这一题来说,单从时间复杂度来算,其实已经算是最优解了,但是,对于常数时间,其实我们是可以继续进行优化的。那就是用数组代替栈,因为数组的寻址是很快的,所以,如果想进一步提升,就需要用数组代替栈去优化常数时间了。这里就直接把代码给大家了,有兴趣的同学可以研究研究。效率提升也还是蛮大的。
public static int sumSubarrayMins(int[] arr) {int[] stack = new int[arr.length];int[] left = nearLessEqualLeft(arr, stack);int[] right = nearLessRight(arr, stack);long ans = 0;for (int i = 0; i < arr.length; i++) {long start = i - left[i];long end = right[i] - i;ans += start * end * (long) arr[i];ans %= 1000000007;}return (int) ans;}public static int[] nearLessEqualLeft(int[] arr, int[] stack) {int N = arr.length;int[] left = new int[N];int size = 0;for (int i = N - 1; i >= 0; i--) {while (size != 0 && arr[i] <= arr[stack[size - 1]]) {left[stack[--size]] = i;}stack[size++] = i;}while (size != 0) {left[stack[--size]] = -1;}return left;}public static int[] nearLessRight(int[] arr, int[] stack) {int N = arr.length;int[] right = new int[N];int size = 0;for (int i = 0; i < N; i++) {while (size != 0 && arr[stack[size - 1]] > arr[i]) {right[stack[--size]] = i;}stack[size++] = i;}while (size != 0) {right[stack[--size]] = N;}return right;}题目二.斐波那契数列
斐波那契数列大家都知道,包括我们要求斐波那契数列第n项,相信大家也都知道,正常我们来求,一个一个算呗,1 1 2 3 5 8 12 ...... 是一个O(n)的方法是最优解吗? 不是,不是最优解,难道还有比O(n)还好的方法嘛,有O(log N) 逆天了,哇,怎么可能呢,你怎么能通过log N解决呢,有可能,来自于哪里,注意,我们都知道斐波那契数列是 F(n) = F(n-1) + F(n - 2) 并且第一项是 1 第二项也是 1 的严格递推式。面对这种除了初始项 剩下项是严格的递推式都有log N的方法。不光是斐波那契数列,只要是严格递推式,都有logN的方法。那什么样的式子没有logN的方法呢,有条件转移的式子没有logN的方法,比如说有个 if else 在这种条件下是一个式子,在另一种条件下又是另一种式子,这种的就没有logN的方法。 这里用到了一点的线性代数,但是它并不难,什么意思呢,就是这样的, F(N) = F(N-1) + F(N-2)的话,第N项和N-1项和N-2项是严格递推关系,那么来看,它减的最多的是谁,是 2 我们说他是一个2阶递推,2阶递推啥意思,我们知道斐波那契数列 F1 = 1, F2 = 1 ,它必存在下列关系。
线性代数就是为了解决严格递推第几项的问题才发明的,所以不要问为什么,这是线性代数的思想基础。同样道理
这个 2 * 2的矩阵到底是啥玩意呢,不知道,我们可以算出来。因为斐波那契数列前几项我们是可以列出来的对不对,来,我们来实际算一下。

有啥用,我们继续往下看。

通过上图我们可以看到,我们如果想求斐波那契数列的第n项,关键点再求某个矩阵的某一个次方,只要你这个矩阵的某个次方算的足够快,我这个斐波那契数列第n项就算的足够快。对不对,那下面这个问题就来了,一个矩阵的n次方怎么算的足够快,我们先看一个特别特别基本的问题,一个数的n次方怎么算最快,比如 10^75 怎么算最快 我们把相同的方式用到矩阵上,算矩阵的n次方不就快了嘛。那10^75怎么算最快呢,如果我们一个一个乘,就需要乘74次,这样就是一个O(n)的方法。它不够快, 75次方的二进制是啥,我们看 75 怎么分解 75 = 64 + 8 + 2 + 1 所以 75的二进制就是 1001011,接下来我们看如下图。

我们先二进制为 1 的位置,代表需要一个 10 的对应的次方。数字的n次方解决了,那矩阵呢,也是一样的。我们看上图最开始 的 1 那么放在矩阵中应该是什么呢,单位矩阵,就是对角线都为 1 ,其余全为 0 的矩阵。
public class FibonacciProblem {public static int f1(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return 1;}return f1(n - 1) + f1(n - 2);}public static int f2(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return 1;}int res = 1;int pre = 1;int tmp = 0;for (int i = 3; i <= n; i++) {tmp = res;res = res + pre;pre = tmp;}return res;}// O(logN)public static int f3(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return 1;}// [ 1 ,1 ]// [ 1, 0 ]int[][] base = { { 1, 1 }, { 1, 0 } };int[][] res = matrixPower(base, n - 2);return res[0][0] + res[1][0];}public static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}// res = 矩阵中的1int[][] t = m;// 矩阵1次方for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = product(res, t);}t = product(t, t);}return res;}// 两个矩阵乘完之后的结果返回public static int[][] product(int[][] a, int[][] b) {int n = a.length;int m = b[0].length;int k = a[0].length; // a的列数同时也是b的行数int[][] ans = new int[n][m];for(int i = 0 ; i < n; i++) {for(int j = 0 ; j < m;j++) {for(int c = 0; c < k; c++) {ans[i][j] += a[i][c] * b[c][j];}}}return ans;}public static void main(String[] args) {int n = 19;System.out.println(f1(n));System.out.println(f2(n));System.out.println(f3(n));System.out.println("===");}}题目三、返回n年后牛的数量
第一年农场有1只成熟的母牛A,往后的每年:
1)每一只成熟的母牛都会生一只母牛
2)每一只新出生的母牛都在出生的第三年成熟
3)每一只母牛永远不会死 返回N年后牛的数量
题目呢很好理解,然后大家观察下面的例子,是不是一下子就看出公式是什么了。
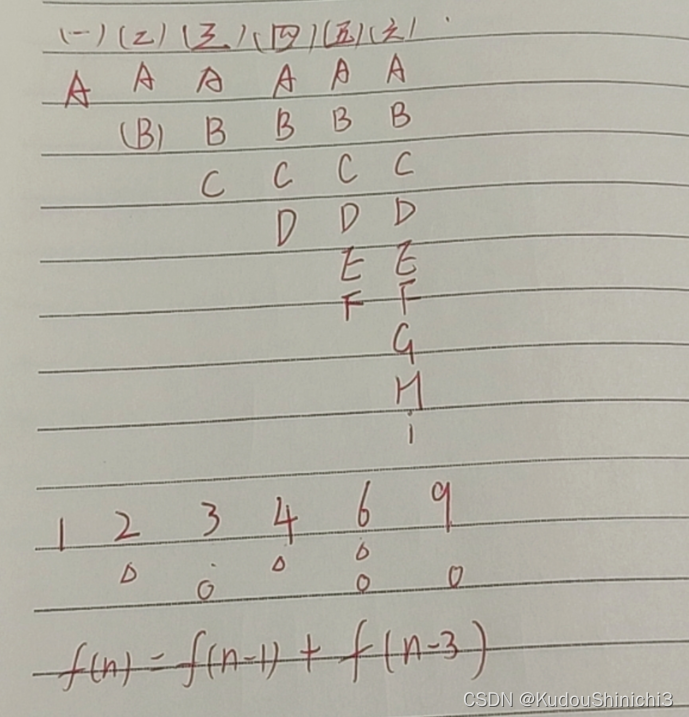
然后我们就开始推这个矩阵是什么
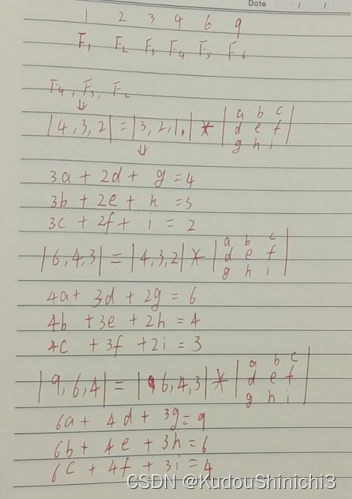
这样是不是就知道矩阵是什么了,看是不是和斐波那契数列一样,接下就知道该怎么办了吧
public class FibonacciProblem {public static int c1(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2 || n == 3) {return n;}return c1(n - 1) + c1(n - 3);}public static int c2(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2 || n == 3) {return n;}int res = 3;int pre = 2;int prepre = 1;int tmp1 = 0;int tmp2 = 0;for (int i = 4; i <= n; i++) {tmp1 = res;tmp2 = pre;res = res + prepre;pre = tmp1;prepre = tmp2;}return res;}public static int c3(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2 || n == 3) {return n;}int[][] base = { { 1, 1, 0 }, { 0, 0, 1 }, { 1, 0, 0 } };int[][] res = matrixPower(base, n - 3);return 3 * res[0][0] + 2 * res[1][0] + res[2][0];}public static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}// res = 矩阵中的1int[][] t = m;// 矩阵1次方for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = product(res, t);}t = product(t, t);}return res;}// 两个矩阵乘完之后的结果返回public static int[][] product(int[][] a, int[][] b) {int n = a.length;int m = b[0].length;int k = a[0].length; // a的列数同时也是b的行数int[][] ans = new int[n][m];for(int i = 0 ; i < n; i++) {for(int j = 0 ; j < m;j++) {for(int c = 0; c < k; c++) {ans[i][j] += a[i][c] * b[c][j];}}}return ans;}public static void main(String[] args) {int n = 19;System.out.println(c1(n));System.out.println(c2(n));System.out.println(c3(n));System.out.println("===");}}题目四、给定一个数N,想象只由0和1两种字符,组成的所有长度为N的字符串 如果某个字符串,任何0字符的左边都有1紧挨着,认为这个字符串达标 返回有多少达标的字符串
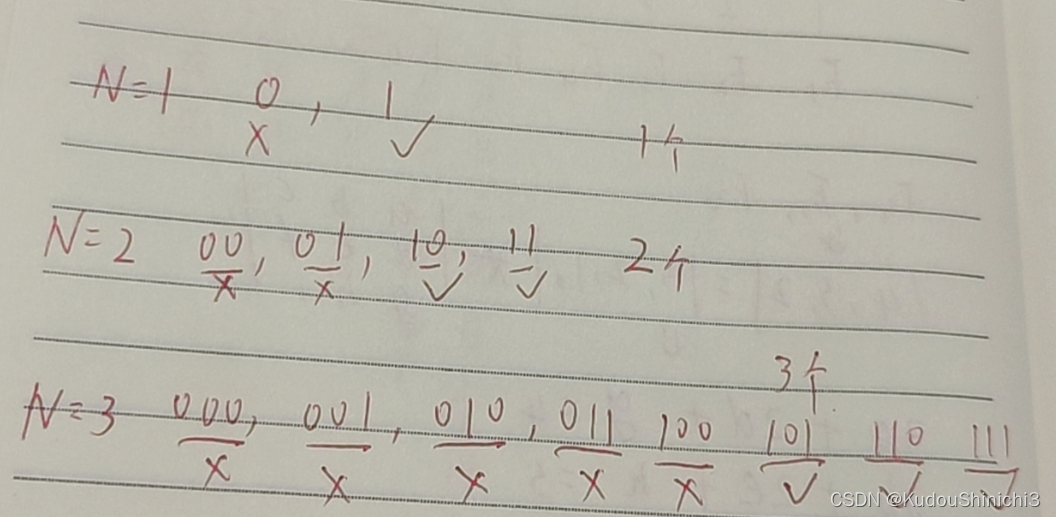
通过观察我们发现,这不就是 初始值为 1 和 2 的斐波那契数列嘛。代码也很简单,就直接给大家了。
public class FibonacciProblem {public static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}// res = 矩阵中的1int[][] t = m;// 矩阵1次方for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = product(res, t);}t = product(t, t);}return res;}// 两个矩阵乘完之后的结果返回public static int[][] product(int[][] a, int[][] b) {int n = a.length;int m = b[0].length;int k = a[0].length; // a的列数同时也是b的行数int[][] ans = new int[n][m];for(int i = 0 ; i < n; i++) {for(int j = 0 ; j < m;j++) {for(int c = 0; c < k; c++) {ans[i][j] += a[i][c] * b[c][j];}}}return ans;}public static int s1(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return n;}return s1(n - 1) + s1(n - 2);}public static int s2(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return n;}int res = 2;int pre = 1;int tmp = 0;for (int i = 3; i <= n; i++) {tmp = res;res = res + pre;pre = tmp;}return res;}public static int s3(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2) {return n;}int[][] base = { { 1, 1 }, { 1, 0 } };int[][] res = matrixPower(base, n - 2);return 2 * res[0][0] + res[1][0];}public static void main(String[] args) {int n = 19;System.out.println(s1(n));System.out.println(s2(n));System.out.println(s3(n));System.out.println("===");}}这篇关于单调栈(续)、由斐波那契数列讲述矩阵快速降幂技巧的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






