本文主要是介绍机器学习算法实践-SVM中的SMO算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
前两篇关于SVM的文章分别总结了SVM基本原理和核函数以及软间隔原理,本文我们就针对前面推导出的SVM对偶问题的一种高效的优化方法-序列最小优化算法(Sequential Minimal Optimization, SMO)的原理进行总结并进行相应的Python实现。
坐标上升算法(Coordinate Ascent)
在SMO算法之前,还是需要总结下坐标上升算法,因为SMO算法的思想与坐标上升算法的思想类似。
坐标上升算法每次通过更新多元函数中的一维,经过多次迭代直到收敛来达到优化函数的目的。简单的讲就是不断地选中一个变量做一维最优化直到函数达到局部最优点。
假设我们需要求解的问题形式为(类似我们SVM的对偶形式):
算法过程伪码:
例子
若我们的优化目标为一个二元函数:
我们先给一个 的初值然后开始迭代。
- 先固定
,把
看做
的一元函数求最优值,可以简单的进行求导获取解析解:
- 在固定x2x2, 把ff看成x1x1的一元函数求最优值,得到x1x1的解析解:
按照上面两个过程不断交替的优化 和
,直到函数收敛。
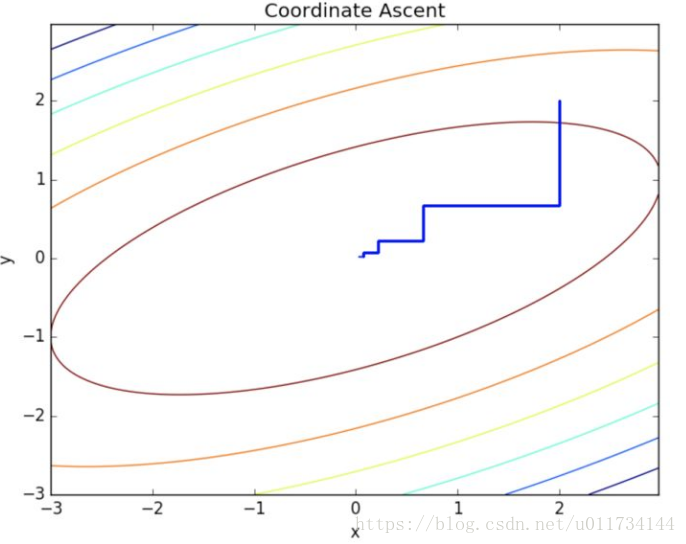
通过下面的图就可以看出,优化的过程,因为每次只优化一个变量,每次迭代的方向都是沿着坐标轴方向的。
因为每次只是做一维优化,所以每个循环中的优化过程的效率是很高的, 但是迭代的次数会比较多。
序列最小优化算法(SMO)
SMO算法介绍
SMO的思想类似坐标上升算法,我们需要优化一系列的αα的值,我们每次选择尽量少的 来优化,不断迭代直到函数收敛到最优值。
来到SVM的对偶问题上,对偶形式:
subject to ,
其中我们需要对 进行优化,但是这个凸二次优化问题的其他求解算法的复杂度很高,但是Platt提出的SMO算法可以高效的求解上述对偶问题,他把原始问题的求解
个参数二次规划问题分解成多个二次规划问题求解,每个字问题只需要求解2各参数,节省了时间成本和内存需求。
与坐标上升算法不同的是,我们在SMO算法中我们每次需要选择一对变量 , 因为在SVM中,我们的
并不是完全独立的,而是具有约束的:
因此一个 改变,另一个也要随之变化以满足条件。
SMO算法原理
获得没有修剪的原始解
假设我们选取的两个需要优化的参数为 , 剩下的
则固定,作为常数处理。将SVM优化问题进行展开就可以得到(把与
无关的项合并成常数项
):
于是就是一个二元函数的优化:
根据约束条件 可以得到
与
的关系:
两边同时乘上 , 由于
得到:
令 ,
,
的表达式代入得到:
后面我们需要对这个一元函数进行求极值, 对
的一阶导数为0得到:
下面我们稍微对上式进行下变形,使得 能够用更新前的
表示,而不是使用不方便计算的
。
因为SVM对数据点的预测值为:
则 以及
的值可以表示成:
已知 , 可得到:
将 的表达式代入到
中可以得到:
我们记 为SVM预测值与真实值的误差:
令 得到最终的一阶导数表达式:
得到:
这样我们就得到了通过旧的 获取新的
的表达式,
便可以通过
得到。
对原始解进行修剪
上面我们通过对一元函数求极值的方式得到的最优 是未考虑约束条件下的最优解,我们便更正我们上部分得到的
为
, 即:
但是在SVM中我们的 是有约束的,即:
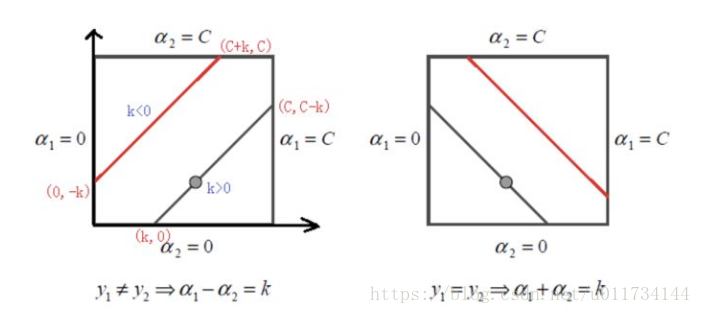
此约束为方形约束(Bosk constraint), 在二维平面中我们可以看到这是个限制在方形区域中的直线(见下图)。
(如左图) 当 时,线性限制条件可以写成:
,根据
的正负可以得到不同的上下界,因此统一表示成:
-
- 下界:
- 上界:
- 下界:
(如右图) 当 时,限制条件可写成:
, 上下界表示成:
-
- 下界:
- 上界:
- 下界:
根据得到的上下界,我们可以得到修剪后的 :
得到了 我们便可以根据
得到
:
OK, 这样我们就知道如何将选取的一对 进行优化更新了。
更新阈值b
当我们更新了一对 之后都需要重新计算阈值
,因为
关系到我们
的计算,关系到下次优化的时候误差
的计算。
为了使得被优化的样本都满足KKT条件,
当 不在边界,即
, 根据KKT条件可知相应的数据点为支持向量,满足
, 两边同时乘上
得到
, 进而得到
的值:
其中上式的前两项可以写成:
当 , 可以得到bnew2b2new的表达式(推导同上):
当 和
都有效的时候他们是相等的, 即
。
当两个乘子 都在边界上,且
时,
之间的值就是和KKT条件一直的阈值。SMO选择他们的中点作为新的阈值:
简化版SMO算法实现
这里我主要针对SMO中已选取的一对 值的优化过程进行下Python实现,其中
的选取直接使用傻瓜的遍历方式,并使用100数据点进行训练。
首先是一些辅助函数,用来帮助加载数据,修剪 的值以及随机选取
def load_data(filename):dataset, labels = [], []with open(filename, 'r') as f:for line in f:x, y, label = [float(i) for i in line.strip().split()]dataset.append([x, y])labels.append(label)return dataset, labels
def clip(alpha, L, H):''' 修建alpha的值到L和H之间.'''if alpha < L:return Lelif alpha > H:return Helse:return alpha
def select_j(i, m):''' 在m中随机选择除了i之外剩余的数'''l = list(range(m))seq = l[: i] + l[i+1:]return random.choice(seq)
为了能在最后绘制SVM分割线,我们需要根据获取的 ,数据点以及标签来获取
的值:
def get_w(alphas, dataset, labels):''' 通过已知数据点和拉格朗日乘子获得分割超平面参数w'''alphas, dataset, labels = np.array(alphas), np.array(dataset), np.array(labels)yx = labels.reshape(1, -1).T*np.array([1, 1])*datasetw = np.dot(yx.T, alphas)return w.tolist()
简化版SMO算法的实现,即便没有添加启发式的 选取,SMO算法仍然有比较多的公式需要实现,我本人按照上文的推导进行实现的时候就因为写错了一个下标算法一直跑不出想要的结果。
此实现主要包含两重循环,外层循环是控制最大迭代步数,此迭代步数是在每次有优化一对αα之后进行判断所选取的 是否已被优化,如果没有则进行加一,如果连续max_iter步数之后仍然没有
被优化,则我们就认为所有的
基本已经被优化,优化便可以终止了.
def simple_smo(dataset, labels, C, max_iter):''' 简化版SMO算法实现,未使用启发式方法对alpha对进行选择.:param dataset: 所有特征数据向量:param labels: 所有的数据标签:param C: 软间隔常数, 0 <= alpha_i <= C:param max_iter: 外层循环最大迭代次数'''dataset = np.array(dataset)m, n = dataset.shapelabels = np.array(labels)# 初始化参数alphas = np.zeros(m)b = 0it = 0def f(x):"SVM分类器函数 y = w^Tx + b"# Kernel function vector.x = np.matrix(x).Tdata = np.matrix(dataset)ks = data*x# Predictive value.wx = np.matrix(alphas*labels)*ksfx = wx + breturn fx[0, 0]while it < max_iter:pair_changed = 0for i in range(m):a_i, x_i, y_i = alphas[i], dataset[i], labels[i]fx_i = f(x_i)E_i = fx_i - y_ij = select_j(i, m)a_j, x_j, y_j = alphas[j], dataset[j], labels[j]fx_j = f(x_j)E_j = fx_j - y_jK_ii, K_jj, K_ij = np.dot(x_i, x_i), np.dot(x_j, x_j), np.dot(x_i, x_j)eta = K_ii + K_jj - 2*K_ijif eta <= 0:print('WARNING eta <= 0')continue# 获取更新的alpha对a_i_old, a_j_old = a_i, a_ja_j_new = a_j_old + y_j*(E_i - E_j)/eta# 对alpha进行修剪if y_i != y_j:L = max(0, a_j_old - a_i_old)H = min(C, C + a_j_old - a_i_old)else:L = max(0, a_i_old + a_j_old - C)H = min(C, a_j_old + a_i_old)a_j_new = clip(a_j_new, L, H)a_i_new = a_i_old + y_i*y_j*(a_j_old - a_j_new)if abs(a_j_new - a_j_old) < 0.00001:#print('WARNING alpha_j not moving enough')continuealphas[i], alphas[j] = a_i_new, a_j_new# 更新阈值bb_i = -E_i - y_i*K_ii*(a_i_new - a_i_old) - y_j*K_ij*(a_j_new - a_j_old) + bb_j = -E_j - y_i*K_ij*(a_i_new - a_i_old) - y_j*K_jj*(a_j_new - a_j_old) + bif 0 < a_i_new < C:b = b_ielif 0 < a_j_new < C:b = b_jelse:b = (b_i + b_j)/2pair_changed += 1print('INFO iteration:{} i:{} pair_changed:{}'.format(it, i, pair_changed))if pair_changed == 0:it += 1else:it = 0print('iteration number: {}'.format(it))return alphas, b
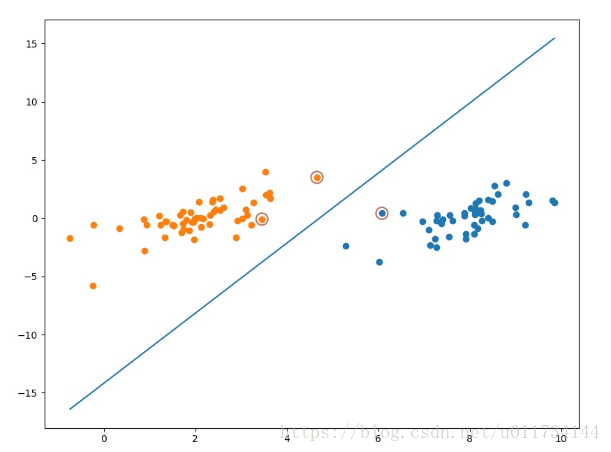
Ok, 下面我们就用训练数据对SVM进行优化, 并对最后优化的分割线以及数据点进行可视化
if '__main__' == __name__:# 加载训练数据dataset, labels = load_data('testSet.txt')# 使用简化版SMO算法优化SVMalphas, b = simple_smo(dataset, labels, 0.6, 40)# 分类数据点classified_pts = {'+1': [], '-1': []}for point, label in zip(dataset, labels):if label == 1.0:classified_pts['+1'].append(point)else:classified_pts['-1'].append(point)fig = plt.figure()ax = fig.add_subplot(111)# 绘制数据点for label, pts in classified_pts.items():pts = np.array(pts)ax.scatter(pts[:, 0], pts[:, 1], label=label)# 绘制分割线w = get_w(alphas, dataset, labels)x1, _ = max(dataset, key=lambda x: x[0])x2, _ = min(dataset, key=lambda x: x[0])a1, a2 = wy1, y2 = (-b - a1*x1)/a2, (-b - a1*x2)/a2ax.plot([x1, x2], [y1, y2])# 绘制支持向量for i, alpha in enumerate(alphas):if abs(alpha) > 1e-3:x, y = dataset[i]ax.scatter([x], [y], s=150, c='none', alpha=0.7,linewidth=1.5, edgecolor='#AB3319')plt.show()
优化最后我们可以看到针对100个数据的 只有少部分是大于零的,即对应的数据点就是支持向量:
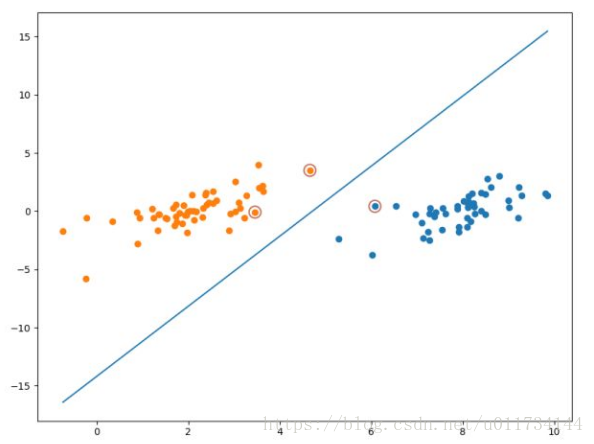
为了能直观的显示支持向量,我将其标注了出来,最终可视化的效果如下图:
总结
本文从坐标上升算法开始介绍,并对SMO算法的原理进行了简单的推导,针对SMO算法中对αα对的优化并使用了Python进行了简化版的SMO实现,并针对小数据集进行了训练得到了对应优化后的SVM。
实现代码以及训练数据链接: https://github.com/PytLab/MLBox/tree/master/svm
原文链接:https://zhuanlan.zhihu.com/p/29212107
这篇关于机器学习算法实践-SVM中的SMO算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!