【数据结构（邓俊辉）学习笔记】二叉搜索树01—

本文主要是介绍【数据结构（邓俊辉）学习笔记】二叉搜索树01——概述，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

1. 纵览
2. 寻关键码访问
3. 有序性
4.单调性
5. 接口

1. 纵览

二叉搜索树将标志着对数据结构的理解进入到一个更深的层次。

回顾向量和列表两类基本数据结构，虽然它们已经可以解决相当多的问题，然而对于进一步的算法设计要求来说，它们都显得力不从心。
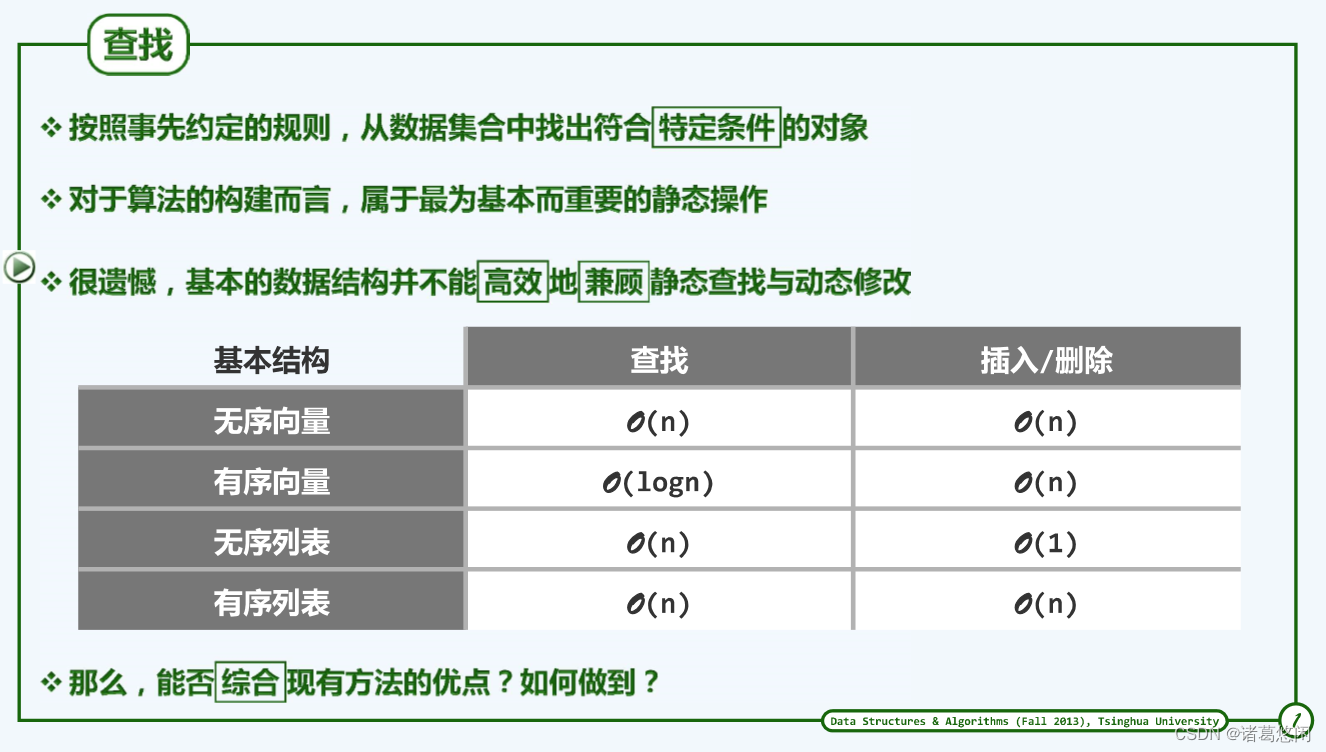
在这里插入图片描述

也正因为此，长久以来最求的目标就是如何将二者的优势结合起来。其实在二叉树上已经做了这方面的尝试，通过对一维列表的拓展引入了所谓的树结构或者二叉树结构。曾经介绍过，从思路上讲，二叉树结构可以认为是二维的列表，可以看作是列表在维度上的一种扩充。

二叉搜索树也就是BST(binary search tree) ，它首先在形式上继承了二叉树，也就是列表结构的特点，同时也巧妙借鉴了向量，或者更准确地讲有序向量的特点和优势，相对而言，后一方面的借鉴更为重要。

如果此前对列表结构的借鉴，只是外表的形式，那么这种对有序向量的借鉴才是一种质的提高。这也是BST相对于其它的数据结构最为传神的部分。

实际上，BST中所有这些传神的部分都集中体现在其中的一个子集，也就是平衡二叉搜索树BBST。经过前人的不断发明和总结，BBST已经成为了一个庞大的家族。在后面将选取其中最具代表性的几个变种，学习学习。

作为整个这部分内容的一个铺垫，在这节中将回答一下几个问题，也就是二叉搜索树是什么？它有什么特点？以及它所提供的接口形式和具体的功能语义？

2. 寻关键码访问

与其他数据结构一样，二叉搜索树也是由一组数据项所构成的集合。然而相对于其他数据结构，二叉搜索树对其中数据项的访问方式却有其鲜明的特点。
在这里插入图片描述

具体来说，其中每一个数据项都拥有各自的关键码key，并以此为特征互相区分，因此在这样一个数据集中，与其说我们在定位数据项，不如说实际上是定位关键码。以汽车为例，每一台汽车都通过它所拥有的车牌号唯一指定，因此这样一种对数据项的访问方式也称作寻关键码访问call-by-key。

当然对于二叉搜索树而言，这种访问方式需要一些先决条件的，具体来说，关键码于关键码之间首先应该能够进行比较，也就是判断孰大孰小，其次，还应支持比对，也就是判断两个关键码是否完全一致。

因此，为了简化和抽象，再接下来的讨论中，不妨假设整个数据集中的数据项都已统一地表示和实现为词条的形式。那么词条也就是entry，究竟是什么呢？

在这里插入图片描述
一般而言，词条结构应该包括以下要素，首先每个词条的确应该拥有一个关键码，而词条所包含的其他信息则笼统归入一个名为value的域，所以简明地说，每一个词条实际上都是由key和value构成的这么样一个组合，也称作pair。

此外正如刚才所言，词条域词条之间应该能够相互比较和比对，如果词条结构原本并不支持这两条就需要对相关操作符进行重载。可以看到，所谓entry之间的比较和比对，按照这种方式，实际上都转化为了词条中关键码的比较和比对。

那么在所有的数据项都已符合这种词条的规范之后，二叉搜索树又当如何定义并且组织呢？

3. 有序性

在这里插入图片描述

在接下来的讨论中，为了简洁起见，都将二叉搜索树Binary Search Tree 简称做BST。

二叉搜索树首先是二叉树，其中的基本组成单位，也就是节点。

每个节点都各自存有一个词条，另外刚才也讲过，每一个词条也都唯一的对应于某一个关键码，因此同样是为了便于叙述和讲解，在此后只要不致引起混淆，往往会将节点、词条以及关键码这三个概念直接等同起来，相互指代，而不加严格区分。

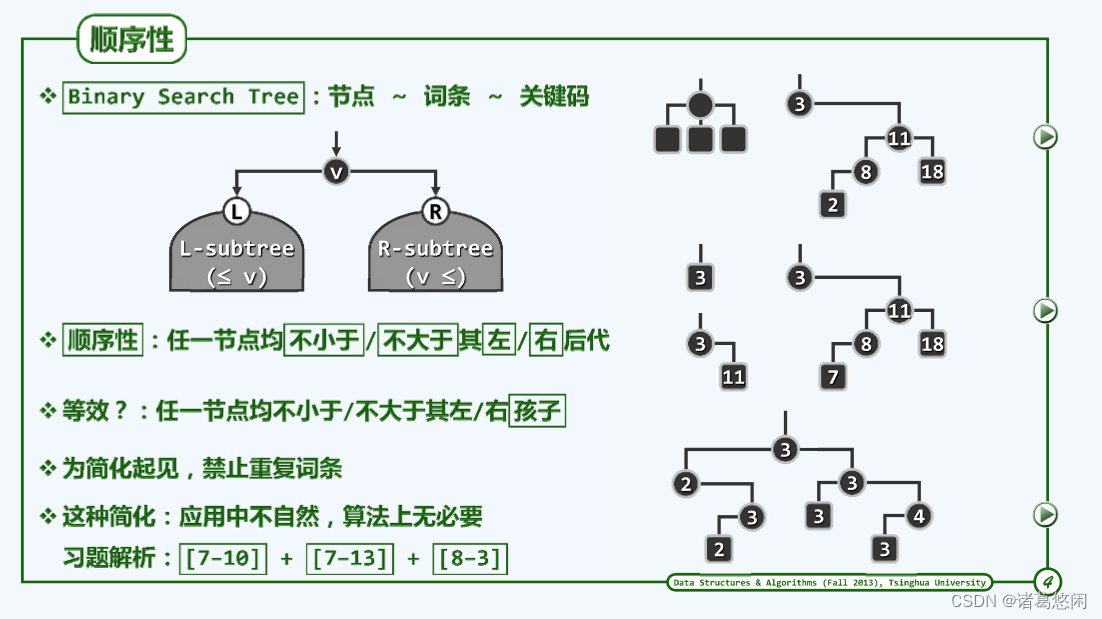
那么相对一般的Binary Tree，BST究竟有什么特点和特征呢？概括起来只有一条，也就是处处满足顺序性。

所谓顺序性具体来说就是相对于某一个节点V而言，如果它的左后代存在，那么所有的左后代都不致比它更大，对称地，如果它的右后代存在，那么所有的右后代都不致比它更小。

来看两个反例

上图最左上角一棵树并非二叉搜索树，因为很明显，相对于这个节点而言，它已经拥有三个孩子，不再是二叉树，更谈不上是二叉搜索树。
上图最右上角，可以看到相对于节点3而言，它的某一个右后代，也就是2，要比它严格地更小，这一点违反了BST的基本要求，所以它并非一棵BST。尽管相对于其它的节点而言，顺序性的确都是满足的，因此如果将关键码2适当地替换为一个稍大的关键码，比如说7，那么就可以使之成为一棵名副其实的BST。

当然BST还有很多边界情况

比如只含单个节点的二叉树，必然是BST。
类似地，即便其中只包含一个单分支，只要它在此局部满足顺序性，那么依然可以称作是一棵BST。

关于顺序性这样一个定义是非常简明而且准确的——任一节点均不小于/不大于其左/右后代。也可略作调整，比如将后代替换成孩子——任一节点均不小于/不大于其左/右孩子。

依然出于简化考虑，还需要补充另一条强制的规定，也就是在树中所存的词条不得彼此重复。

这样所有的不小于都可以直接简化为大于，而所有的不大于都可以直接简化为小于。

然而这种假设在实际应用中极不自然，同时在算法设计方面也是无需回避的一个问题。实际上完全可以在接下来所要介绍的方法的基础上略作扩充，使得BST能够支持同时存在多个雷同词条。

最后回过头来重新审视如上所定义的顺序性，不难发现，这只是一个局部性的特征，那么这样一种局部性特征对于BST整体而言又意味着什么呢？

4.单调性

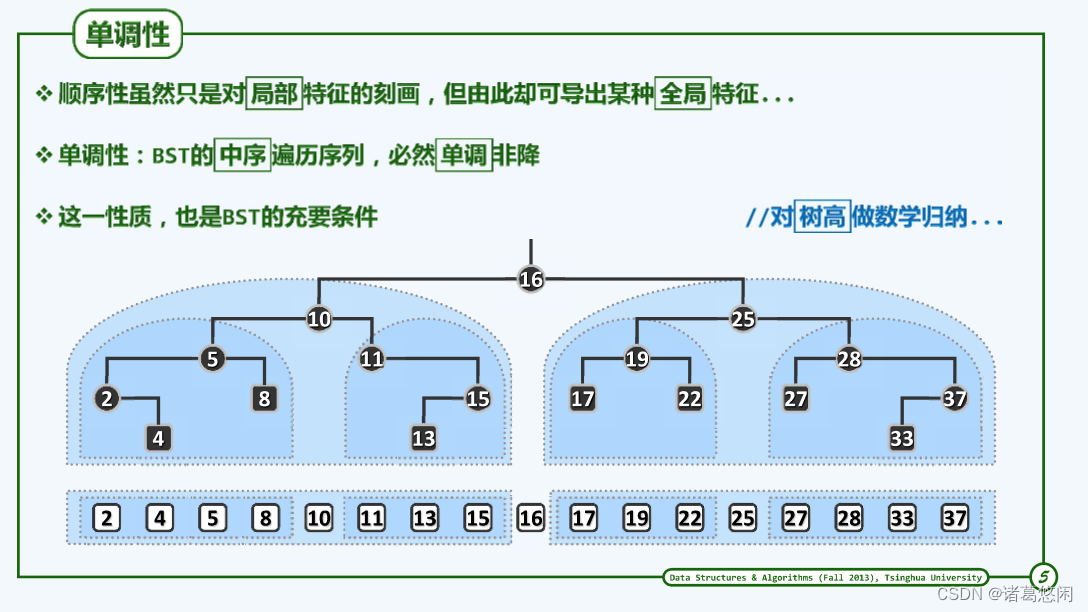
在这里插入图片描述
尽管此前所定义的顺序性只不过是处处局部的一个特征，但正如马上就会看到的，这样一种局部性特征，居然可以导出BST 整体全局性的某种特征。具体来说，也就是所谓的单调性。

实际上只要考差BST的中序遍历序列，就会发现它必然是单调的。

看下上面实例，在树中的每一个顶点处顺序性都是满足的，接下来不妨沿着中序遍历序列浏览所有节点，可以看到，所有这些节点，的确是以它们的关键码为序，单调排列。

实际上任何一棵BST都具有这样的一个特征，反过来具有这一特征的任何二叉树，也必然同时是一棵BST。

不妨来证明其中必要性，对于任何一棵BST首先考查它的树根，自然的在这个树根位置顺序性必须得到满足，这就意味着左子树中的所有节点都不至大于树根，而右子树中的所有节点也不至于小于树根，而根据中序遍历的规则，左子树对应的遍历子序列不然严格位于树根节点的左侧，而右子树对应的遍历子序列也必然严格位于树根节点的右侧，所以在整棵树的遍历子序列中，位于树根节点左侧的所有节点都不致比它更大，对称地，位于树根节点右侧的所有节点也都不致比它更小，也就是说在根节点处，整个遍历序列是满足单调性的。

那么至于左子树对应的遍历子序列和右子树所对应的遍历子序列通过数学归纳，不难证明在它们各自的内部，也是处处满足这种单调性。

因此，如果在绘制二叉树的时候，能够保证相对于每一个顶点，它的左子树和右子树都绘制于它的左和右侧，那么就可以简明地判定这棵树是否是一棵BST。为此，只需考查所有节点地垂直投影，所有这些节点投影所构成地序列，其实就是这棵树的中序遍历序列。因此，只要这个序列是单调变化的，那么原二叉树就必然是一棵BST，反之亦然。

因此BST特征可以概括为，在微观上处处满足顺序性，而在宏观上整体满足单调性。

那么作为一种抽象数据类型，BST又该提供哪些标准接口呢？这些接口的具体形式又该如何呢？