【动态规划】| 详解路径问题之地下城游戏力扣174 (困难题)

本文主要是介绍【动态规划】| 详解路径问题之地下城游戏力扣174 (困难题)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🎗️ 主页：小夜时雨
🎗️专栏：动态规划
🎗️如何活着，是我找寻的方向

1. 题目解析

题目链接: https://leetcode.cn/problems/minimum-path-sum/description/
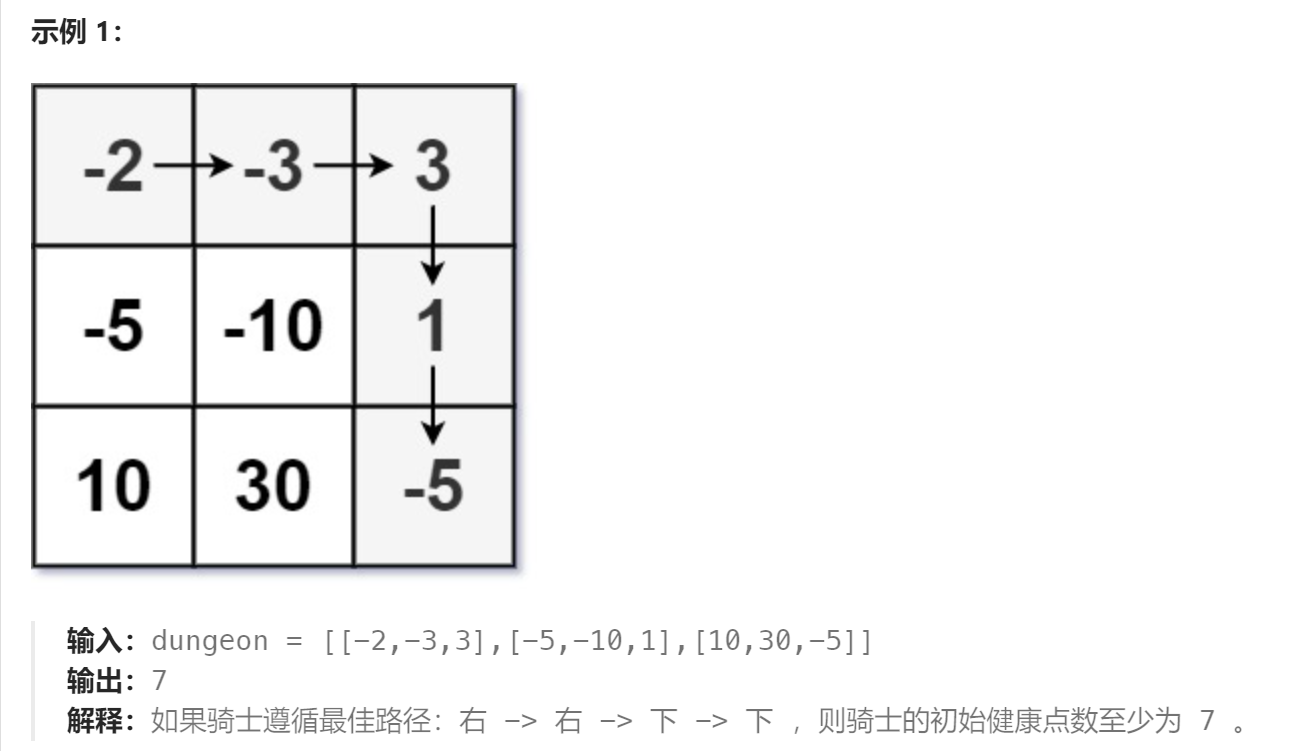
在这里插入图片描述

建议先看一下前面的几道题加深理解一下，本道题是一个反方向思考
不同路径1 ：https://leetcode.cn/problems/unique-paths/description/
不同路径2： https://blog.csdn.net/Jin__Wang/article/details/139623230
最小路径和：https://blog.csdn.net/Jin__Wang/article/details/139653515

这道题的难度是困难, 要是把前面文章关于路径问题的题之后，这道题理解起来还是可以的，与常规的题目是正好相反的，具体地一一介绍。

通常动态规划的题目有五个大步骤进行解析, 本道题也不例外我们来一一进行分析。

1. 状态表示

动态规划的重点是状态表示, 我们通过状态表示才可以写出正确的状态转移方程, 状态表示我们通常都是根据 经验+题目 要求来进行定义的.

但是注意本道题目用我们之前的经验来定义状态表示，后续是推导不出来状态转移方程的。

比如本道题又是一个二维的矩阵, 可以以另一种经验来定义状态表示：即从某个位置为起点，达到终点 + 题目要求。
以本题为例，状态表示可以写为：

dp[i][j]: 从 (i, j) 这个位置出发，到达终点, 所需的最低健康点数

和之前的状态表示是反过来的，之前都是以（i，j）为终点，本题则是表示为起点。

2. 状态转移方程

根据状态表示, （i，j）是起点，那么就可以往下走到达（i + 1， j）位置，或者往右走到达（i，j + 1）位置。
根据状态表示, dp[i][j] 的大小可以由两部分组成, 问的是最低点数, 那么共有两条不同的路径: 从往右走或者从往下走，求的应该是这二者中的最小值。
从 (i, j) 走到终点所需的最低点数为 dp[i][j] , 那么从 (i + 1, j) 走到走到终点所需的最低点数为 dp[i + 1][j], 因为要求点数必须是正整数，所以有 dp[i][j]+ nums[i][j] >= dp[i + 1][j], 才能走到终点。同理 dp[i][j + 1] 也是.
那么 dp[i][j] >= dp[i + 1][j] - nums[i][j]. 这是往下走的情况，往右走的情况同理，求二者中的最小值。

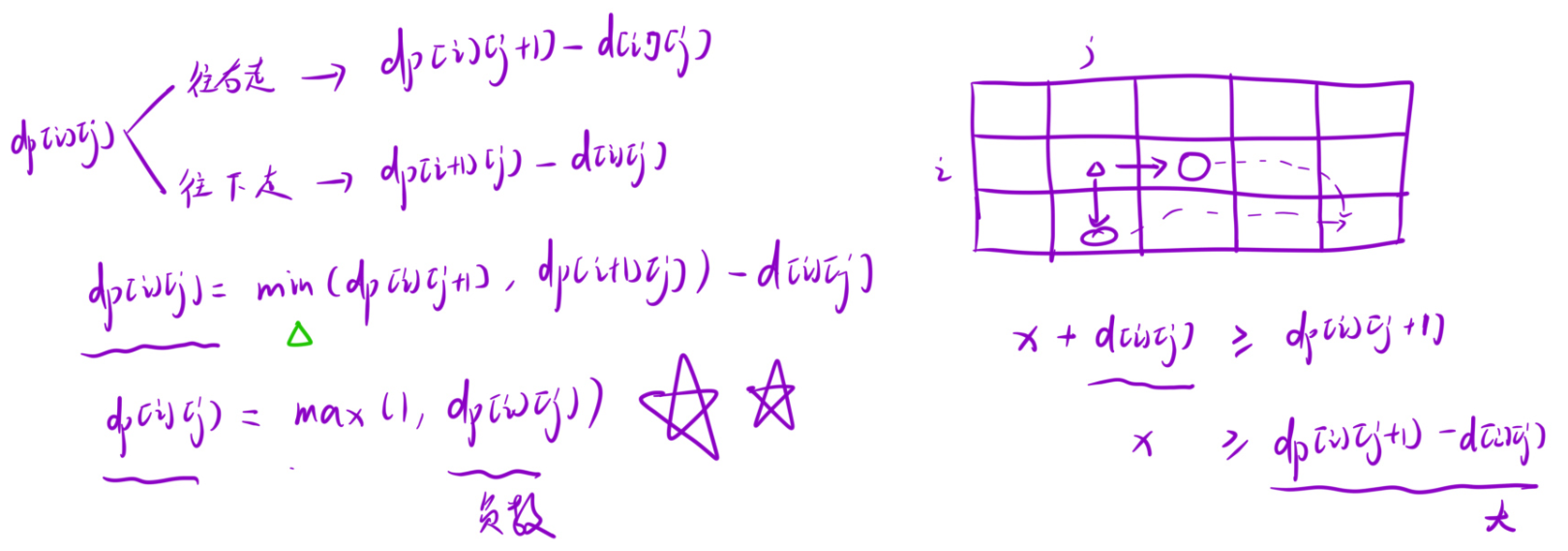
dp[i][j] = Math.min(dp[i + 1][j]，dp[i][j + 1]) - nums[i][j]

细节问题：题目要求点数必须为正整数，有可能计算出来的 dp[i][j] 为一个负数，
表示最低点数是一个负值，然后到达（i，j）是一个超大的正数，加上之后走到了终点，不符合实际情况，所以血量至少为1，所以多加一个比较条件。dp[i][j] > 0的时候没变化， <=0 的时候则会设置为1。
所以状态转移方程应该为：

dp[i][j] = Math.min(dp[i + 1][j]，dp[i][j + 1]) - nums[i][j]
dp[i][j] = Math.max(1，dp[i][j)

细节问题2: 前面几题都提过的下标映射.这里和不同路径1 不同的是，这里需要用到原数组，我们通常也是采取多加一行一列的方式来避免出现 dp 表越界的情况，所以要注意映射关系。
但是因为我们是加的是最后一行和最后一列，遍历也是反过来的，所以下标还是对应上的，所以遍历 dp 表填表的过程中的（i, j）对应原数组的值是 nums[i][j]。和之前还是不一样

在这里插入图片描述

3. 初始化

细节问题: 观察状态转移方程可知, 有可能会有越界的风险, 此处我们依旧采取一种多加一行一列的方式来进行初始化.多加一行一列要保证两点:

虚拟节点的值要保证后面的dp 表里的值是正确的
要注意下标的映射关系. 因为我们是多加了一行一列, 所以对应到原始数组就应该行列要减一. (此处用到了原数组, 所以要有这个映射关系)

注意：
这道题的初始化和前几道题依旧是相反的。

注意到我们计算 dp[i][j] 的时候是用到下一行的数据和本行右侧的数据，所以填表顺序也是反的，初始化也是反的，需要初始化最后一行最后一列。

本题的初始化方式和最小路径和类似，不过初始位置是最后一行最后一列。
最小路径和：https://blog.csdn.net/Jin__Wang/article/details/139653515
根据实际情况来，救完公主到达（m, n）位置后，往右走或者往下走，保证救完公主之后的点数最低为1，所以 dp[m][n - 1] = dp[m - 1][n] = 1
其余的位置因为求的是最小值，所以不要干扰到结果，应该和最小路径和一样其余位置更新为最大值
例如观察下图我们发现，填写 dp[1][1] 的时候需要用到左边和上边值，因为求的是二者中的最小值，为了不干扰结果，设置为0即可。
看下图，但是填写 dp[m - 1][n - 2] 的时候，需要用到下面的值 dp[m][n - 2] 和 dp[m - 1][n - 1] 作比较求最小值，倘如是dp[m][n - 2] 还是默认初始化为 0 的话，就会影响结果，有可能使 dp[m - 1][n - 2] = dp[m][n - 2] - nums[m - 1][n - 1, 此时dp[m][n - 2] 为0，就导致错误了.
实际情况应该是 dp[m - 1][n - 2] 本该是只有一条路径，那就是从到（m - 1，n - 2）走到（m - 1，n - 1），就应该是 dp[m - 1][n - 2] = dp[m - 1][n - 1] - nums[m - 1][n - 1]. 观察结果，因为求一个最小值，让 dp[m][n - 2] 是一个非常大的数字，不影响结果即可。此处通常我们设置为整数最大值或者 0x3f3f3f3f.

看图更容易理解
在这里插入图片描述

4. 填表顺序

观察可知, 填 (i, j) 的值的时候需要用到下一行和右边的值. 所以填表顺序是从下往上, 从右往左.

5. 返回值

根据题目的要求, 从起点（0，0）要到达(m, n) 的最小健康点数, 正好对应 dp[0][0] 的表示. 所以返回 dp[0][0] 即可，和之前的题目返回值也是不同的。

2. 代码

这道题难在思路都是反过来的，5个分析的过程和之前都是不一样的。

动态规划的代码编写一般都是分为 4 个步骤进行:

创建 dp 表
初始化
填表
返回值

   // 完全跟前面的题完全反过来了: 包括状态表示, 方程, 和填表顺序public int calculateMinimumHP(int[][] dungeon) {// ×××××××dp[i]状态表示: 从起点左上角到达（i，j） 位置的最小健康点数 这种找不出状态方程××××// dp[i]状态表示: 从（i，j） 位置到达终点所需的最小健康点数// 1.创建 dp表// 2.初始化// 3.填表// 4.返回值// 动态规划 这里的是二维, 所以时空都是O(M*N)int m = dungeon.length, n = dungeon[0].length;int[][] dp = new int[m + 1][n + 1];// 初始化， 新加的最右边一列和最下边一列// 都需要进行初始化为最大值 (因为求的是最小值, 默认的0有可能干扰结果)for(int i = 0; i <= m; i++) dp[i][n] = Integer.MAX_VALUE; //新增行for(int j = 0; j <= n; j++) dp[m][j] = Integer.MAX_VALUE; //新增列// dp[0][1] = dp[1][0] = 0; // 特殊处理边界dp[m][n - 1] = dp[m - 1][n] = 1;// 做好映射关系, 这里因为添加的是右下角的行和列, 所以不需要映射// 这里填的是 dp 表, 所以建议从(1,1) 开始. 也就是dp表多加了一行一列// 遍历的是 dp 表for(int i = m - 1; i >= 0; i--) { // 从xia往上每一行 和之前反过来了for(int j = n - 1; j >= 0; j--) { // 从you往左每一列// dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + dungeon[i - 1][j - 1]; 这是之前的写法, 这道题是反过来的dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = Math.max(1, dp[i][j]); //细节问题:防止血量有负数}}// return dp[m][n];return dp[0][0];}