本文主要是介绍ceisum只聚合效果展示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
忙于开发三维引擎的扩展功能,实在时间太少了,仓促截几张图,看一下聚合效果。
1.聚合又文字标签
四种效果:如下
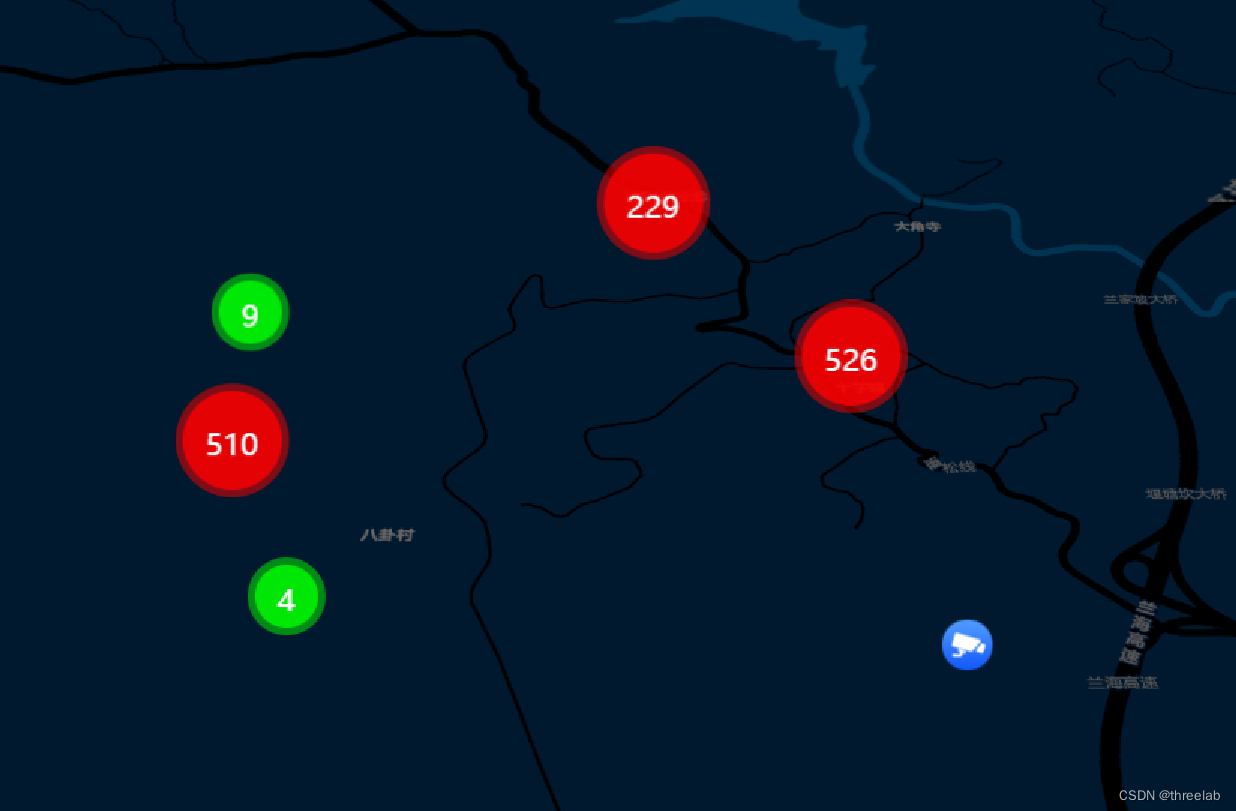
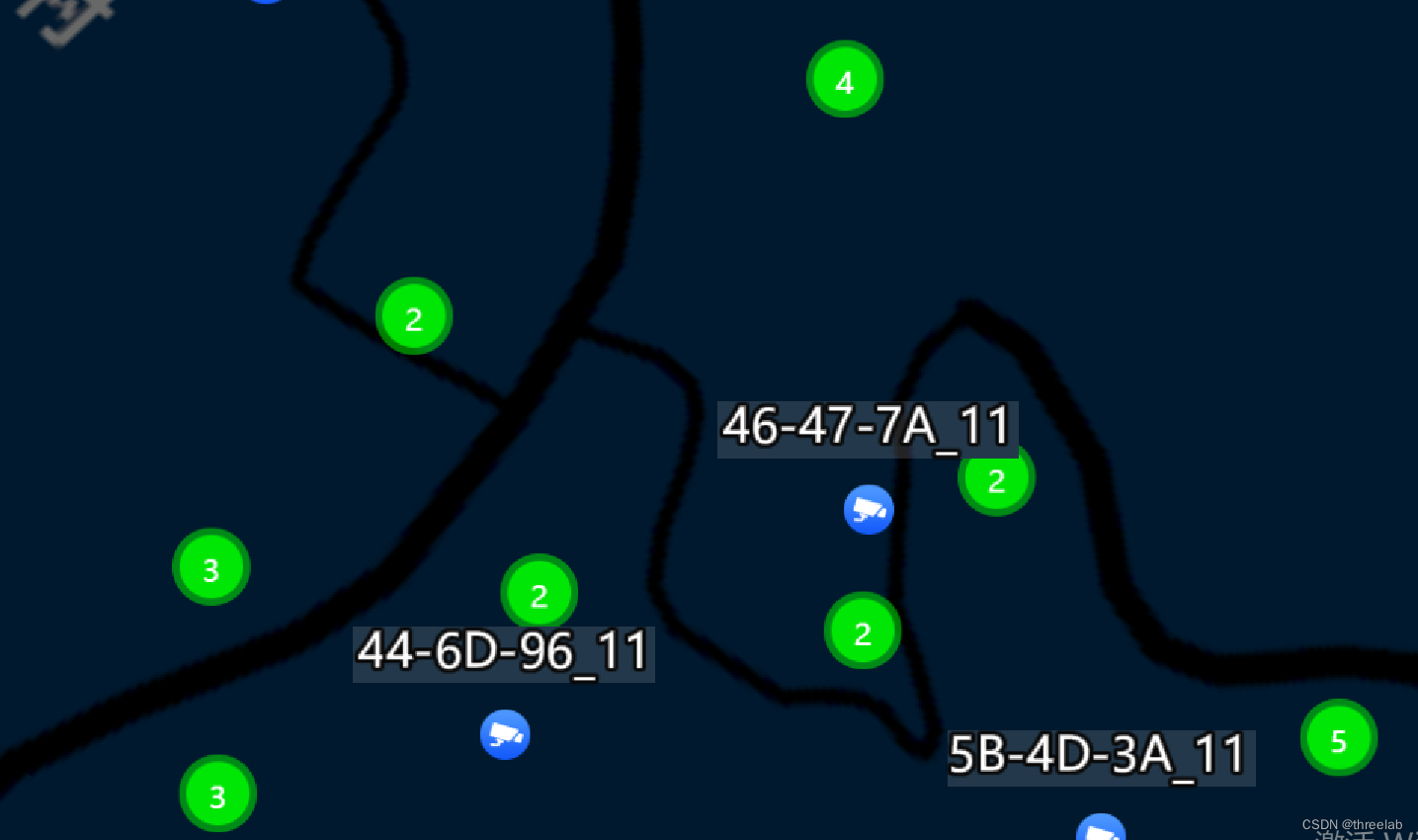
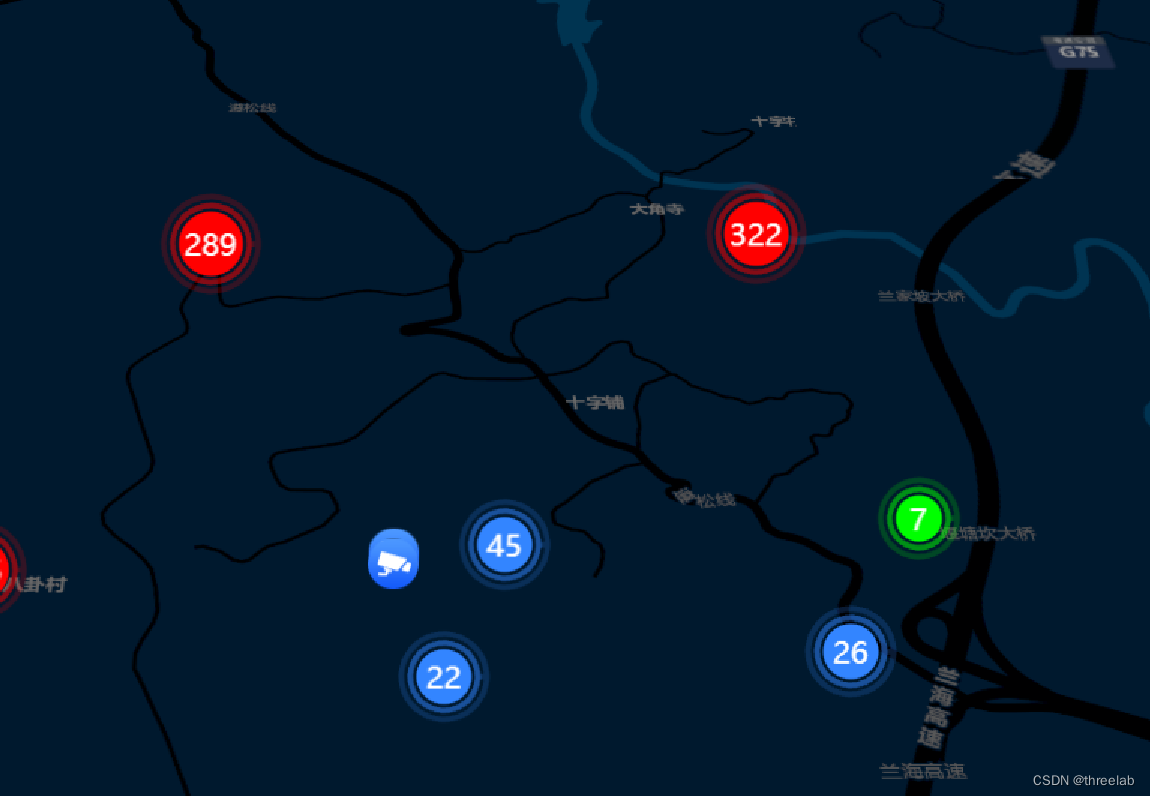
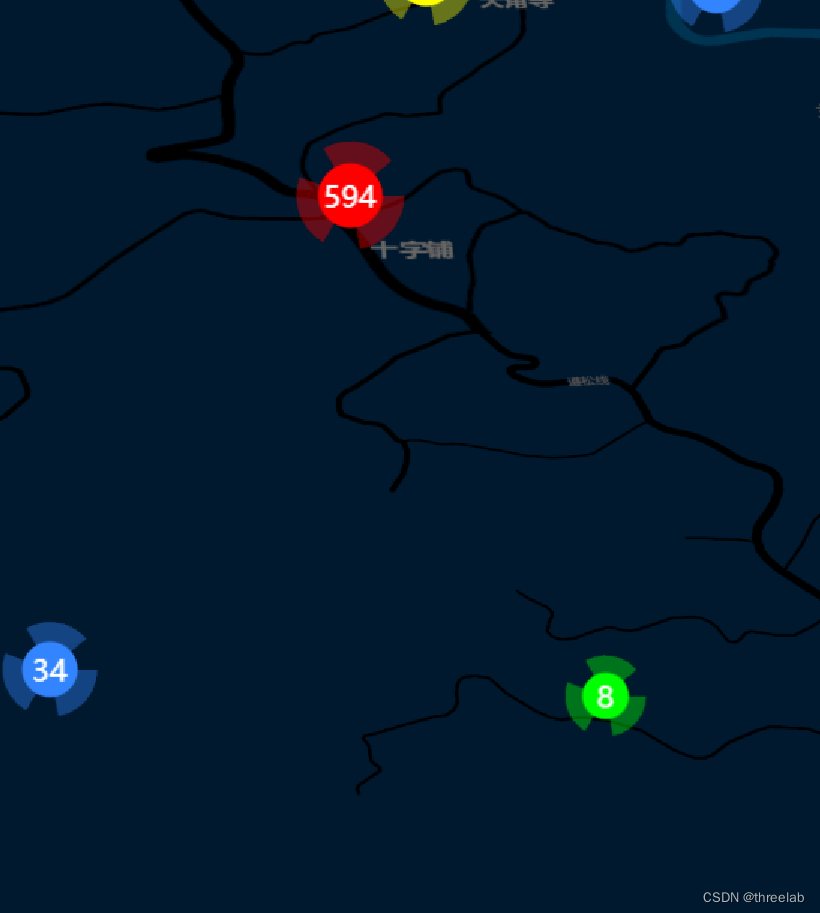
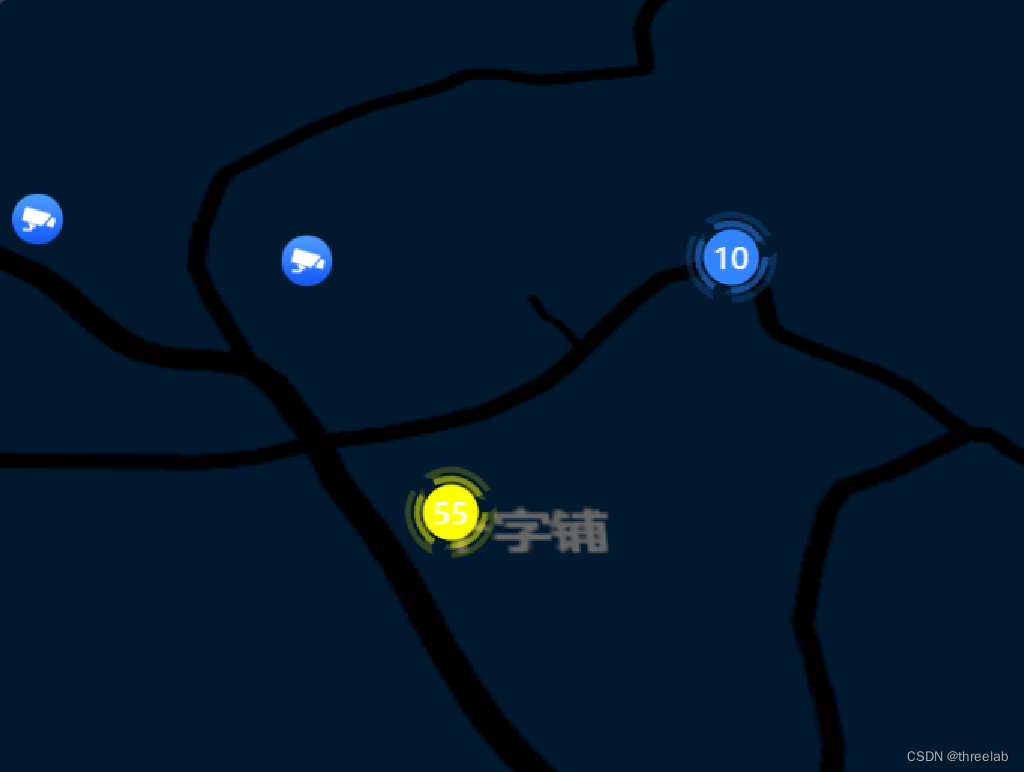
2.聚合无文字标签
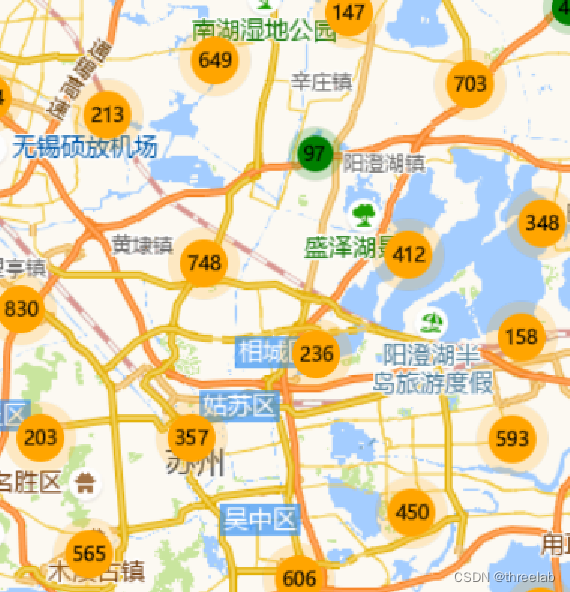
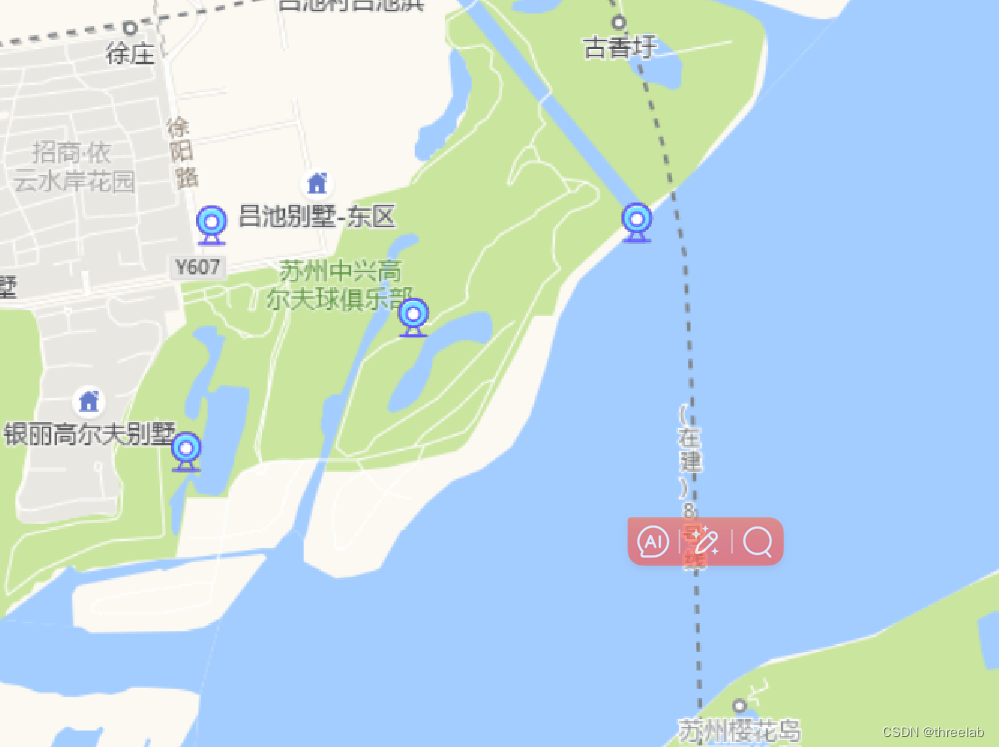
这篇关于ceisum只聚合效果展示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
本文主要是介绍ceisum只聚合效果展示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
忙于开发三维引擎的扩展功能,实在时间太少了,仓促截几张图,看一下聚合效果。
1.聚合又文字标签
四种效果:如下





2.聚合无文字标签


这篇关于ceisum只聚合效果展示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
http://www.chinasem.cn/article/1061667。
23002807@qq.com