OpenCV学习(4.13) 霍夫变换

本文主要是介绍OpenCV学习(4.13) 霍夫变换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.霍夫变换

霍夫变换（Hough Transform）是图像处理中的一种技术，主要用于检测图像中的直线、圆或其他形状。它通过将图像空间中的点映射到参数空间来实现，这样，图像空间中在同一直线上的点在参数空间中会形成一条曲线，而这条曲线上的交点对应于图像空间中的直线。
霍夫变换的基本思想是：

对于图像中的每一个边缘点，考虑它可能属于的所有候选直线。
对于每一条候选直线，使用霍夫变换算法在参数空间中对其进行投票。
投票最多的候选直线即为检测到的直线。

霍夫变换有几种变体，包括：

- 霍夫直线变换：用于检测图像中的直线。
- 霍夫圆变换：用于检测图像中的圆。
- 霍夫椭圆变换：用于检测图像中的椭圆。

霍夫变换的优点是它对噪声和图像间断有一定的鲁棒性，但缺点是计算量大，特别是对于霍夫圆变换，因为需要考虑三个参数（圆心坐标和半径）。因此，在实际应用中，通常会采用一些优化技术来减少计算量，例如使用图像金字塔或限制参数范围。

2. 霍夫线变换

在这一章当中，

我们将理解霍夫变换的概念。
我们将看到如何使用它来检测图像中的线条。
我们将了解以下函数： cv.HoughLines（） ， cv.HoughLinesP（）

如果您能够以数学形式表示该形状，则霍夫变换是一种用于检测任何形状的流行技术。它可以检测到形状，即使它被破坏或扭曲一点点。我们将看到它如何适用于生产线。

一条线可以表示为 $$y = mx+c$$ 或以极坐标形式 $$\rho = x \cos \theta + y \sin \theta$$ 表示为其中 $$\rho$$ 是垂线从原点到直线的距离。$$\theta$$ 是这条垂直线形成的角度，水平轴是逆时针测量的（该方向因你代表坐标系而变化。这种表示用于 OpenCV ）。检查下图：

所以如果这条线经过原点以下，它会有一个小于 180 度的正角度。如果它在原点上方，我们不是取一个大于 180 的角，而是取一个小于 180 的负角度。任何垂直线都是 0 度，水平线是 90 度。

现在我们来看看霍夫变换是怎么作用于直线的。任何线都可以被表示成这两项(r,θ) 。所以首先它创建了一个二维数组，或者是累加器(来保存这两个参数的值)然后他设置(r,θ) 作为初始值。令(二维数组的)行表示r，令列表示 θ 。数组的大小取决于你需要的精准度。假设说你想要角度的精度是精确到 1 度，那你就需要 180 列。而对于r来说，最大可能的距离是图像的对角线长度。因此，要精确到一个像素的程度，行数应该是图像的对角长度。

想象有一张 100x100 的图像，它上面有一条水平的线条在图像正中间。取这条线的第一个点，你知道它的坐标 (x,y)值。现在，按照这条直线的等式，把值θ = 0,1,2,...,180带入，并且查看你获取到的r值。对每一对(r,θ) ，我们都把它们在累加器中对应的值计数增加 1。而此时，在这个计数器中，单元 (50,90) 和其他单元一样计数等于 1。

现在去这条线上的第二个点，重复上面的步骤。增加单元中你拿到的对应的值(rho, theta)。这一次，单元(50,90)的计数增到到了 2。你实际上做的是投票投出(r,θ) 值。你不断为这条直线上所有的点继续这个过程。在每一个点，单元(50,90)都会得票，而其他的单元有可能会得票，也有可能不会。按这个方案，最终单元 (50,90) 会获得最高的投票(译者注：在 100X100 的图像正中水平的直线到原点距离为 50，垂角 90 度)。所以最终搜索我们的累加器来找最高得票的单元，我们就会取到 (50,90)，这就说明图像中有一条线距离原点垂距 50，它过原点的垂线和水平线夹角为 90 度。这个过程很好的显示在了以下的动画中

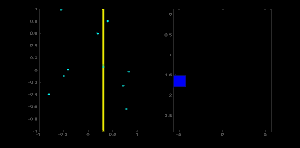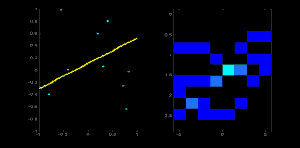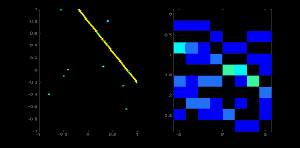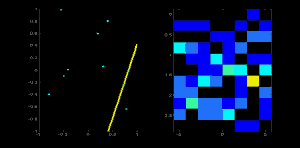
这就是霍夫变化针对直线工作的原理。非常简单，也许你可以用 Numpy 自己来实现它。以下是一张显示了累加器的图像。在某些地方的亮点说明它们是图像中可能线条的参数。

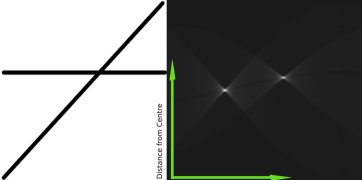
2. 1 OpenCV中的霍夫变换

上面解释的这一堆东西，在 OpenCV 里都封装起来成为**cv.HoughLines（）** 函数了。它简单的返回了一个(rho, theta)`值得数组。$$\rho$$ 的单位是像素，$$\theta$$的单位是弧度。第一个参数，输入图像应该是个二元图像，所以在应用霍夫线性变换之前先来个阈值法或者坎尼边缘检测。第二、第三参数分别是 $$\rho$$ 和 $$\theta$$ 的精度。第四个参数则是一个阈值，它代表了一个$$(\rho,\theta)$$单元被认为是一条直线需要获得的最低票数。要记住的是，得票数其实取决于这条直线穿过了多少个点。所以它也代表了应被检测出的线条最少有多长。

霍夫变换作用于直线的过程通常指的是霍夫直线变换（Hough Line Transform），它是一种在数字图像中检测直线的常用技术。霍夫直线变换的基本思想是将图像空间中的直线映射到参数空间中的点上，从而将直线检测问题转化为在参数空间中寻找交点的问题。
霍夫直线变换的具体步骤如下：
1. **边缘检测**：首先，使用边缘检测算法（如Canny边缘检测）找到图像中的边缘像素。
2. **参数空间投票**：对于每个边缘像素，考虑所有可能的直线方程，通常是直线方程的极坐标形式：$ r = x \cos(\theta) + y \sin(\theta) $，其中 $ (r, \theta) $ 是参数空间中的点，$ (x, y) $ 是图像空间中的边缘像素坐标。对于每个 $ (x, y) $ ，在参数空间中画出对应的所有 $ (r, \theta) $ 曲线。
3. **累加和阈值**：在参数空间中，对于每个可能的 $ (r, \theta) $ 对，累加器数组中的一个单元被增加。当多个边缘像素对应的曲线在参数空间中相交于同一点时，该点的累加器值会很高。
4. **检测峰值**：在累加器数组中，峰值对应于图像中的直线。设置一个阈值，只有超过这个阈值的累加器值才被认为是检测到的直线。
5. **提取直线**：对于每个检测到的峰值，其对应的 $ (r, \theta) $ 值可以用来确定图像空间中的一条直线。
霍夫直线变换的优点是它对图像中的直线断裂和噪声不敏感，能够检测出图像中所有的直线，无论其方向如何。然而，这种方法的一个缺点是计算量大，特别是对于高分辨率图像。此外，它通常只适用于检测直线，而不适用于检测曲线或其他复杂的形状。对于这些情况，需要使用霍夫变换的其他变体，如霍夫圆变换或广义霍夫变换。

import cv2 as cv
import numpy as np
img = cv.imread(cv.samples.findFile('sudoku.png'))
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray,50,150,apertureSize = 3)
lines = cv.HoughLines(edges,1,np.pi/180,200)
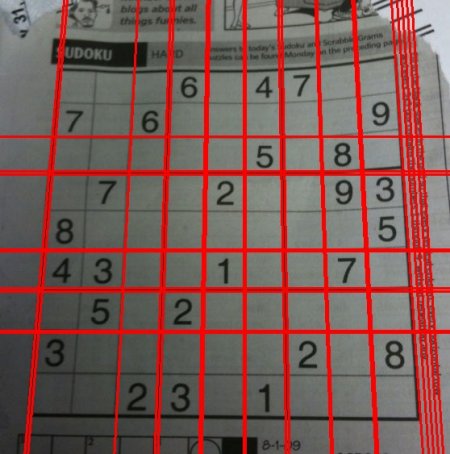
for line in lines:rho,theta = line[0]a = np.cos(theta)b = np.sin(theta)x0 = a*rhoy0 = b*rhox1 = int(x0 + 1000*(-b))y1 = int(y0 + 1000*(a))x2 = int(x0 - 1000*(-b))y2 = int(y0 - 1000*(a))cv.line(img,(x1,y1),(x2,y2),(0,0,255),2)
cv.imwrite('houghlines3.jpg',img)

检查以下结果：

2.2 概率Hough变换

概率Hough变换（Probabilistic Hough Transform）是标准Hough变换的一种改进版本，它用于检测图像中的直线，但是相比于标准Hough变换，它更加高效，因为它不需要遍历整个参数空间。概率Hough变换通过随机选择图像空间中的边缘点，并只考虑这些点对应的参数空间中的少量可能直线，从而减少了计算量。
概率Hough变换的基本步骤如下：
1. **边缘检测**：与标准Hough变换一样，首先使用边缘检测算法找到图像中的边缘像素。
2. **随机采样**：从检测到的边缘点中随机选择一个点。
3. **局部峰值搜索**：对于选中的边缘点，在参数空间中搜索其可能的直线参数。这一步通常是通过在较小的邻域内进行累加器投票来实现的。
4. **累加器阈值**：如果参数空间中的某个局部区域的累加器值超过了设定的阈值，则认为找到了一条直线。
5. **重复过程**：重复步骤2到4，直到所有的边缘点都被考虑过，或者达到了某种停止条件（如找到了足够的直线）。
6. **结果验证**：最后，可能需要对检测到的直线进行验证，以确保它们是真实的直线，而不是由噪声或错误的边缘检测引起的假阳性。
概率Hough变换相比于标准Hough变换的优点是它更快，因为它不需要为每个边缘点计算和投票所有的参数空间。此外，它通常能够给出更准确的结果，因为它考虑了边缘点之间的局部关系。这种方法的缺点是它可能不会检测到图像中所有的直线，特别是当直线的支持点较少时。因此，概率Hough变换适用于直线较为密集的场景，而在直线稀疏的情况下可能不如标准Hough变换有效。

在霍夫变换中，你可以发现即使是一条仅有两个参数的直线，也需要用到大量的计算。概率霍夫变换是我们已知的，针对霍夫变换的优化方案。它不去取所有的点来列入考虑，取而代之的是取足够完成直线检测的这些点的随机子集。只要我们把阈值下调一点。下图在霍夫空间中比较了霍夫变换与概率霍夫变换。

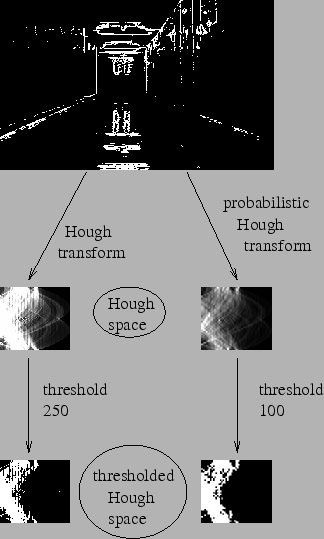
OpenCV 实现基于使用 Matas，J。和 Galambos，C。和 Kittler，J.V。 [133] 的渐进概率 Hough 变换的线的鲁棒检测。使用的函数是 cv.HoughLinesP（） 。它比之前介绍的函数多出来两个参数：

minLineLength - 最小线长。比这个值小的线条会被丢弃。
maxLineGap - 允许线段之间的最大间隙，以便将(在同一条直线上的)线段视为同一条。

最好的是，它直接返回直线的两个端点。在前面的例子中，你只得到直线的参数，你必须找到所有的点。而这个方法，一切都是那么的直接和简单。

import cv2 as cv
import numpy as np
img = cv.imread(cv.samples.findFile('sudoku.png'))
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray,50,150,apertureSize = 3)
lines = cv.HoughLinesP(edges,1,np.pi/180,100,minLineLength=100,maxLineGap=10)
for line in lines:x1,y1,x2,y2 = line[0]cv.line(img,(x1,y1),(x2,y2),(0,255,0),2)
cv.imwrite('houghlines5.jpg',img)

3. 霍夫圆变换

在这一章当中，

我们将学习使用霍夫变换来查找图像中的圆圈。
我们将了解这些函数： cv.HoughCircles（）

圆圈在数学上表示为$(x-x_{center})^2 + (y - y_{center})^2 = r^2$其中$(x_{center},y_{center})$是圆的中心，$r$ 是圆的半径。从这个公式来看，得知我们有三个参数，这样我们就需要一个三维度的累加器来做霍夫变换了，这样效率是非常低的。所以 OpenCV 用了更巧妙的方法Hough Gradient Method ，它利用了边缘的梯度信息。

霍夫圆变换（Hough Circle Transform）是霍夫变换的一种变体，专门用于检测图像中的圆。与霍夫直线变换不同，霍夫圆变换需要检测三个参数：圆心坐标 $ (x, y) $ 和半径 $ r $。这导致参数空间成为三维的，因此计算量相对较大。
霍夫圆变换的基本步骤如下：

1. **图像预处理**：首先对图像进行滤波和边缘检测，以突出圆的特征。
2. **参数空间投票**：对于每个边缘点，考虑所有可能的半径大小，对于每个可能的半径，计算圆心可能的位置，并在三维参数空间中对应的 $ (x, y, r) $ 处进行投票。
3. **累加和峰值检测**：在参数空间中，累加器数组中的值表示找到圆的可能性。累加器数组中的局部峰值对应于图像中的圆。设置一个阈值，只有超过这个阈值的累加器值才被认为是检测到的圆。
4. **提取圆心和半径**：对于每个检测到的峰值，其对应的 $ (x, y, r) $ 值可以用来确定图像空间中的一个圆。

由于霍夫圆变换的计算量很大，实际应用中通常会采用一些启发式方法来减少搜索空间，例如限制半径的范围或使用图像金字塔进行多尺度检测。
霍夫圆变换的优点是它对图像中的圆具有一定的鲁棒性，即使圆不完整或存在一定的噪声也能检测出来。然而，它的计算量大，且对噪声敏感，因此在实际应用中需要根据具体情况选择合适的参数和预处理步骤。

我们在这里使用的函数是 cv.HoughCircles（） 。它的参数非常的多，这些参数在文档中都有详细的解释。所以我们直接上代码吧。

import numpy as np
import cv2 as cv
img = cv.imread('opencv-logo-white.png',0)
img = cv.medianBlur(img,5)
cimg = cv.cvtColor(img,cv.COLOR_GRAY2BGR)
circles = cv.HoughCircles(img,cv.HOUGH_GRADIENT,1,20,param1=50,param2=30,minRadius=0,maxRadius=0)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:# draw the outer circlecv.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)# draw the center of the circlecv.circle(cimg,(i[0],i[1]),2,(0,0,255),3)
cv.imshow('detected circles',cimg)
cv.waitKey(0)
cv.destroyAllWindows()

结果如下图所示：