【智能算法应用】基于粒子群算法的多尺度Retinex图像去雾方法

本文主要是介绍【智能算法应用】基于粒子群算法的多尺度Retinex图像去雾方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.算法原理

【智能算法】粒子群算法（PSO）原理及实现

多尺度Retinex算法

在Retinex算法中，雾化图像的形成可以总结为入射光和反射光的乘积:
$I(x,y)=L(x,y)\times R(x,y)\tag{1}$
其中，I(x,y)表示图像亮度，R(x,y)和L(x,y)分别代表反射分量和照明分量。
用于模拟周围环境的函数类似于通常用于单个神经元感受野的高斯差分函数：
$L(x,y)=I(x,y)*F(x,y)\tag{2}$
周围函数F(x,y)：
$F(x,y)=K\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\tag{3}$
其中，σ 是高斯周围空间尺度参数。下面展示不同σ 高斯函数图像，较大的σ 将强调色彩保真度但失去更多图像细节信息，而较小的 σ 则相反。
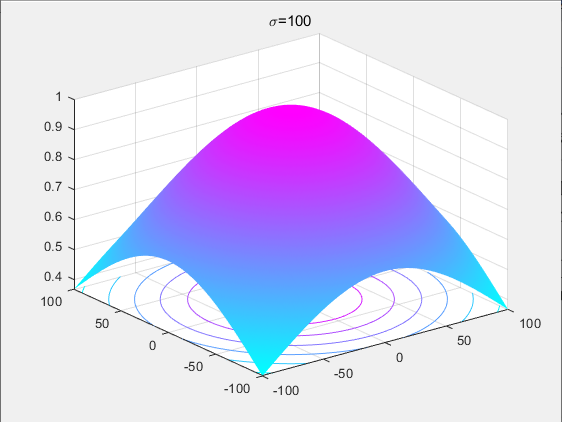
在这里插入图片描述

单尺度Retinex (single-scale Retinex, SSR) 算法:
$\begin{aligned}&r_{SSR,i}(x,y)=\mathrm{log}R_{i}(x,y)\\&=\log(I_{i}(x,y))-\log(F_{i}(x,y)*I_{i}(x,y))\end{aligned}\tag{4}$

多尺度Retinex（Multi-scale Retinex, MSR) 被提出来通过不同尺度的加权叠加来抵消单一尺度的影响:
$\begin{aligned}&R_{msr,i}=\sum_{n=1}^{N}w_{n,i}r_{n,i}\\&=\sum_{n=1}^{N}w_{n,i}\big(\log(I_{i}(x,y))-\log\big(F_{n,i}(x,y)*I_{i}(x,y)\big)\big)\end{aligned}\tag{5}$

2.粒子群算法的多尺度Retinex图像去雾方法

考虑到去雾后的图像颜色自然，细节清晰和信息保留，适应度函数定义为:
$\mathrm{PSNR}=20\cdot\log_{10}\left(\frac{\mathrm{MAX}_{I}}{\sqrt{\mathrm{MSE}}}\right)$

3.结果展示

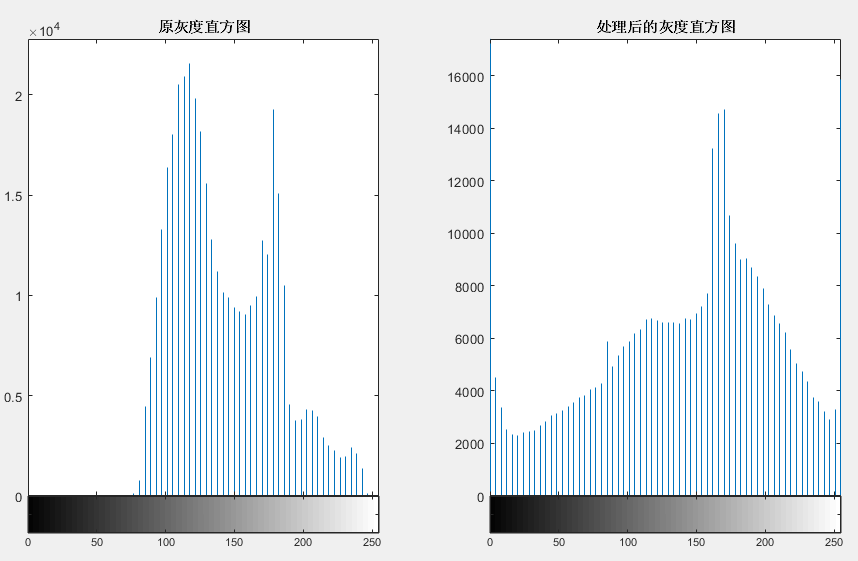
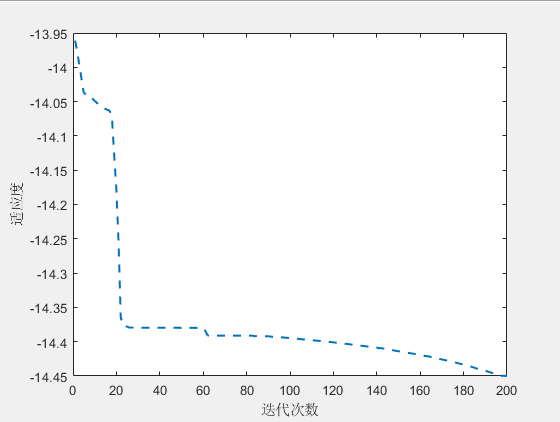
在这里插入图片描述

4.参考文献

[1] Yao L P, Pan Z. The Retinex-based image dehazing using a particle swarm optimization method[J]. Multimedia Tools and Applications, 2021, 80(3): 3425-3442.