本文主要是介绍基于MATLAB仿真的BCC卷积码维特比译码算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
🧑🏻个人简介:具有3年工作经验,擅长通信算法的MATLAB仿真和FPGA实现。代码事宜,私信博主,程序定制、设计指导。
🚀基于MATLAB仿真的BCC卷积码维特比译码算法
目录
🚀1.BCC卷积码概述
🚀2.维特比译码算法
🚀2.1概述
🚀2.2算法核心思想
🚀2.3算法优缺点
🚀2.4应用实例
🚀2.5部分源代码和仿真截图
🚀1.BCC卷积码概述
BCC卷积码是一种非分组码,它在1955年被提出。卷积码在编码时是把k个比特的信息段编写成n个比特的码组,但其监督码元不仅与当前编码比特信息有关,还与前面(N-1)个比特有关,其中N为卷积码的编码约束度。卷积码通常记为(n, k, N)。
根据卷积码的特性,它更适合用于前向纠错,并且在许多实际情况下其效果优于分组码。此外,卷积码运算简单,尤其适合用在被高斯白噪声所干扰的传输信道中。
🚀2.维特比译码算法
🚀2.1概述
维特比译码算法是一种卷积码的解码算法,它在1967年被提出。该算法主要基于信道的统计特性以及卷积码的特性来进行解码,因此得到了广泛应用,特别是在卫星通信领域、蜂窝网通信系统和无线局域网(WLAM)中。
🚀2.2算法核心思想
网格图与路径:卷积码的编码过程与网格图中的一条路径对应,即输入序列的编码过程与网格图中的路径一一对应。当输入序列长度为x时,网格中有2^x条不同的路径和编码器的2^x种发送序列对应。
分支度量与幸存路径:在每个符合输入的分支中,都可以计算出分支度量值(通常使用汉明距或欧氏距离等方法)。算法会将到达节点的两条路径进行对比,并选择度量值小的一条作为幸存路径。
累积与回溯:随着数据的接收,算法会累积每条幸存路径的度量值。在译码结束时,从所有幸存路径中选择一条度量值最小的路径进行回溯,从而得出译码输出。
🚀2.3算法优缺点
优点:维特比译码算法解码方法简单,复杂度低。
缺点:随着约束长度N的增加,算法的复杂度呈2^N增长。因此,当N很大时,维特比算法的复杂度会非常高,不适合用于解码。通常,维特比译码算法适用于约束长度小于10的场合。
🚀2.4应用实例
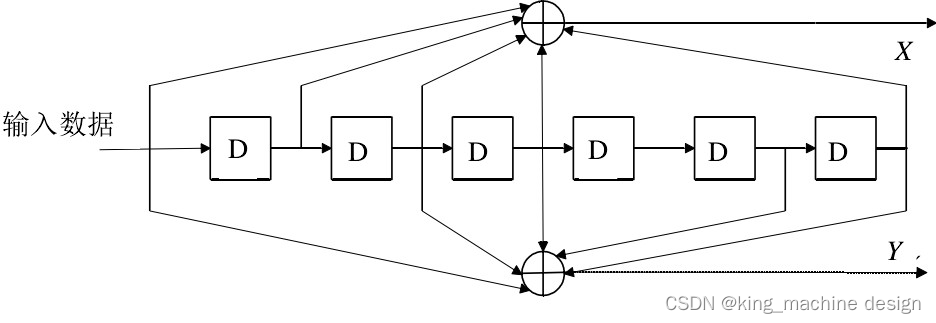
以(2,1,7)卷积码为例,当编码器约束长度为7时,编码器有7个延迟器的状态(0,1),这些状态组成了编码器的64个状态。在解码过程中,算法需要对每个时刻接收到的数据进行64次比较,从64条幸存路径中选择出度量值最小的一条进行回溯,得出译码输出。

举个简单的例子,如图所示(2,1,7)卷积码,生成多项式为(133,171),发送序列为11,得到编码输出为1110。接收端接收到1110后,开始估算发送的信息序列。由于移位寄存器初始状态时,其值为全0,这是已知的。故假设发送的信息序列的第一位为0,则编码输出的结果为00,则对比接收到的第一个输出11,他们的汉明距离为2,此时由汉明距离可估算出第一位发送的信息比特为1,但是这样就没有利用上后面的编码数据,有较高的概率出错。所以,根据第一位发送信息比特为0和1这两种情况,继续算下一位信息比特输入时的编码输出,并且比较它们的汉明距离。容易得出共有4种可能的发送信息序列:00、01、10、11,对应的汉明距离为3、3、2、0。很明显最小的汉明距离为0,对应的发送信息序列为11,与正确的序列一致。以上可以理解为是维特比算法的硬解码过程,接收端得到的数据都是0和1,汉明距离也都为整数。
🚀2.5部分源代码和仿真截图
部分源代码如下
% 清除所有
clc;clear all;close all;
EbN0_dB = 0:0.2:1; %设置仿真信噪比
FRAMES_NUM = 50;%每种信干比情况下,进行FRAMES_NUM次试验
RATE=1/2;
data_times = 1;message = randi([0 1],1,100);随机产生比特数据
encodeData = convenc(message,trel);%编码
decoded1 = vitbiDecoder_minMetric(receiveSignal,trel,tblen);%译码%画图
BER = bitError/FRAMES_NUM/70/data_times;
BER2 = bitError2/FRAMES_NUM/70/data_times;
plot(EbN0_dB,BER);
title('译码误比特率随信噪比的变化');
xlabel('信噪比');
ylabel('误比特率');仿真图如下
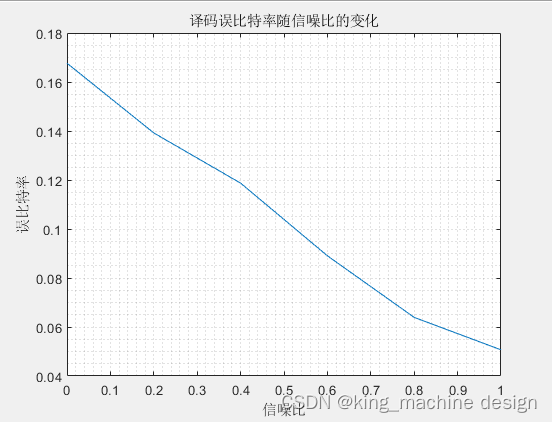
这篇关于基于MATLAB仿真的BCC卷积码维特比译码算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









