本文主要是介绍斯坦福CS229(吴恩达授)学习笔记(6),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
CS229-notes4
- 说明
- 正文
- Problem Set #2: Kernels, SVMs, and Theory
- 5. Uniform convergence
说明
此笔记 是cs229-notes4讲义中的学习内容,与B站上的“09 经验风险最小化”视频对应,主要是该部分对应的习题解答。
课程相关视频、讲义等资料可参照《斯坦福CS229(吴恩达授)学习笔记(1)》 获取。
正文
Problem Set #2: Kernels, SVMs, and Theory
5. Uniform convergence

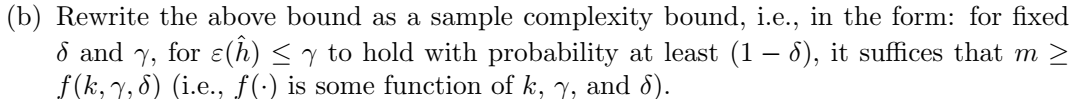
解答:
问题是说,如果有先验知识得知 H \mathcal{H} H中存在使得 m i n i ε ( h i ) = 0 min_i\varepsilon(h_i)=0 miniε(hi)=0的 h i h_i hi,那么是可以给 ε ( h ^ ) \varepsilon(\hat h) ε(h^)求得一个比 2 1 2 m l o g 2 k δ 2\sqrt{\frac{1}{2m}log\frac{2k}{\delta}} 22m1logδ2k更小的上界,即 1 m l o g k δ \frac{1}{m}log\frac{k}{\delta} m1logδk。
可证明 1 m l o g k δ ≤ 2 1 2 m l o g 2 k δ \frac{1}{m}log\frac{k}{\delta}\leq2\sqrt{\frac{1}{2m}log\frac{2k}{\delta}} m1logδk≤22m1logδ2k。
1 m l o g k δ 2 1 2 m l o g 2 k δ = 1 m 2 ( l o g k δ ) 2 4 2 m l o g 2 k δ = ( l o g k δ ) l o g k δ 2 m ( l o g k δ + l o g 2 ) = l o g k δ 2 m ( 1 + l o g 2 l o g k δ ) \begin{aligned} \frac{\frac{1}{m}log\frac{k}{\delta}}{2\sqrt{\frac{1}{2m}log\frac{2k}{\delta}}}=&\sqrt{\frac{\frac{1}{m^2}(log\frac{k}{\delta})^2}{\frac{4}{2m}log\frac{2k}{\delta}}}=\sqrt{\frac{(log\frac{k}{\delta})log\frac{k}{\delta}}{2m(log\frac{k}{\delta}+log2)}}=\sqrt{\frac{log\frac{k}{\delta}}{2m(1+\frac{log2}{log\frac{k}{\delta}})}} \end{aligned} 22m1logδ2k
这篇关于斯坦福CS229(吴恩达授)学习笔记(6)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







